Question Number 153342 by Rankut last updated on 06/Sep/21

Commented by Rankut last updated on 06/Sep/21

$${help}\:\:{please} \\ $$
Answered by liberty last updated on 06/Sep/21
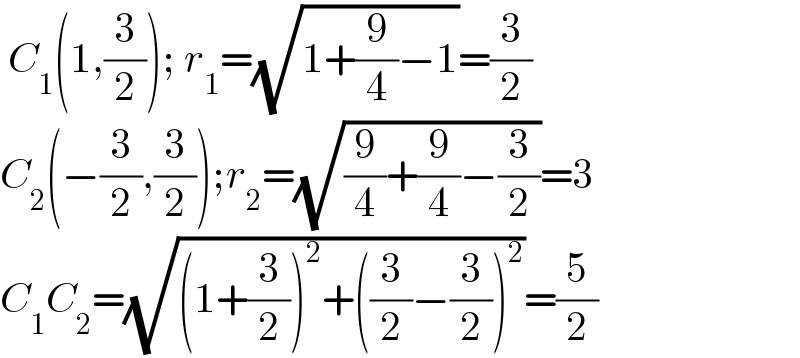
$$\:{C}_{\mathrm{1}} \left(\mathrm{1},\frac{\mathrm{3}}{\mathrm{2}}\right);\:{r}_{\mathrm{1}} =\sqrt{\mathrm{1}+\frac{\mathrm{9}}{\mathrm{4}}−\mathrm{1}}=\frac{\mathrm{3}}{\mathrm{2}} \\ $$$${C}_{\mathrm{2}} \left(−\frac{\mathrm{3}}{\mathrm{2}},\frac{\mathrm{3}}{\mathrm{2}}\right);{r}_{\mathrm{2}} =\sqrt{\frac{\mathrm{9}}{\mathrm{4}}+\frac{\mathrm{9}}{\mathrm{4}}−\frac{\mathrm{3}}{\mathrm{2}}}=\mathrm{3} \\ $$$${C}_{\mathrm{1}} {C}_{\mathrm{2}} =\sqrt{\left(\mathrm{1}+\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{3}}{\mathrm{2}}−\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} }=\frac{\mathrm{5}}{\mathrm{2}} \\ $$
Commented by Rankut last updated on 06/Sep/21

$${thank}\:{you}\:{brother} \\ $$
Answered by Jonathanwaweh last updated on 06/Sep/21
![let x^2 +y^2 −2x−3y+1=0⇔x^2 −2x+y^2 −3y+1=0 ⇔(x−1)^2 −1^2 +(y−(3/2))−((3/2))^2 +1=0 ⇔(x−1)^2 +(y−(3/2))^2 =((3/2))^2 we then have Ω(1;(3/2)) is the center of this circle on the other hand 2x^2 +2y^2 +6x−6y+3=0⇔2x^2 +6x+2y^2 −6y+3=0 ⇔2[(x^2 +3x)]+2[(y^2 −3y)]+3=0 ⇔2[(x+(3/2))^2 −((3/2))^2 ]+2[(y−(3/2))^2 −((3/2))^2 ]+3=0 ⇔2(x+(3/2))^2 −(9/2)+2(y−(3/2))^2 −(9/2)+3=0 ⇔2(x+(3/2))^2 +2(y−(3/2))^2 =6 ⇔(x+(3/2))^2 +(y−(3/2))^2 =3 we then have O(−(3/2);(3/2)) is the center of this circle i)so therefore the distance between the center the two circles is OΩ=(√((−(3/2)−1)^2 +((3/2)−(3/2))^2 )) =(5/2) ii)easy question](https://www.tinkutara.com/question/Q153353.png)
$${let}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{2}{x}−\mathrm{3}{y}+\mathrm{1}=\mathrm{0}\Leftrightarrow{x}^{\mathrm{2}} −\mathrm{2}{x}+{y}^{\mathrm{2}} −\mathrm{3}{y}+\mathrm{1}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Leftrightarrow\left({x}−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{1}^{\mathrm{2}} +\left({y}−\frac{\mathrm{3}}{\mathrm{2}}\right)−\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} +\mathrm{1}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Leftrightarrow\left({x}−\mathrm{1}\right)^{\mathrm{2}} +\left({y}−\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} =\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$${we}\:{then}\:{have}\:\Omega\left(\mathrm{1};\frac{\mathrm{3}}{\mathrm{2}}\right)\:{is}\:{the}\:{center}\:{of}\:{this}\:{circle} \\ $$$${on}\:{the}\:{other}\:{hand}\:\mathrm{2}{x}^{\mathrm{2}} +\mathrm{2}{y}^{\mathrm{2}} +\mathrm{6}{x}−\mathrm{6}{y}+\mathrm{3}=\mathrm{0}\Leftrightarrow\mathrm{2}{x}^{\mathrm{2}} +\mathrm{6}{x}+\mathrm{2}{y}^{\mathrm{2}} −\mathrm{6}{y}+\mathrm{3}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Leftrightarrow\mathrm{2}\left[\left({x}^{\mathrm{2}} +\mathrm{3}{x}\right)\right]+\mathrm{2}\left[\left({y}^{\mathrm{2}} −\mathrm{3}{y}\right)\right]+\mathrm{3}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\Leftrightarrow\mathrm{2}\left[\left({x}+\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} −\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} \right]+\mathrm{2}\left[\left({y}−\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} −\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} \right]+\mathrm{3}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\Leftrightarrow\mathrm{2}\left({x}+\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} −\frac{\mathrm{9}}{\mathrm{2}}+\mathrm{2}\left({y}−\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} −\frac{\mathrm{9}}{\mathrm{2}}+\mathrm{3}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\Leftrightarrow\mathrm{2}\left({x}+\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} +\mathrm{2}\left({y}−\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} =\mathrm{6} \\ $$$$\:\:\:\:\:\:\:\Leftrightarrow\left({x}+\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} +\left({y}−\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} =\mathrm{3} \\ $$$${we}\:{then}\:{have}\:{O}\left(−\frac{\mathrm{3}}{\mathrm{2}};\frac{\mathrm{3}}{\mathrm{2}}\right)\:{is}\:{the}\:{center}\:{of}\:{this}\:{circle} \\ $$$$\left.{i}\right){so}\:{therefore}\:{the}\:{distance}\:{between}\:{the}\:{center}\:{the}\:{two}\:{circles} \\ $$$${is}\:{O}\Omega=\sqrt{\left(−\frac{\mathrm{3}}{\mathrm{2}}−\mathrm{1}\right)^{\mathrm{2}} +\left(\frac{\mathrm{3}}{\mathrm{2}}−\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{5}}{\mathrm{2}} \\ $$$$\left.\:{ii}\right){easy}\:{question}\:\:\:\:\:\: \\ $$$$\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\: \\ $$
Commented by Rankut last updated on 06/Sep/21

$${thanks} \\ $$
