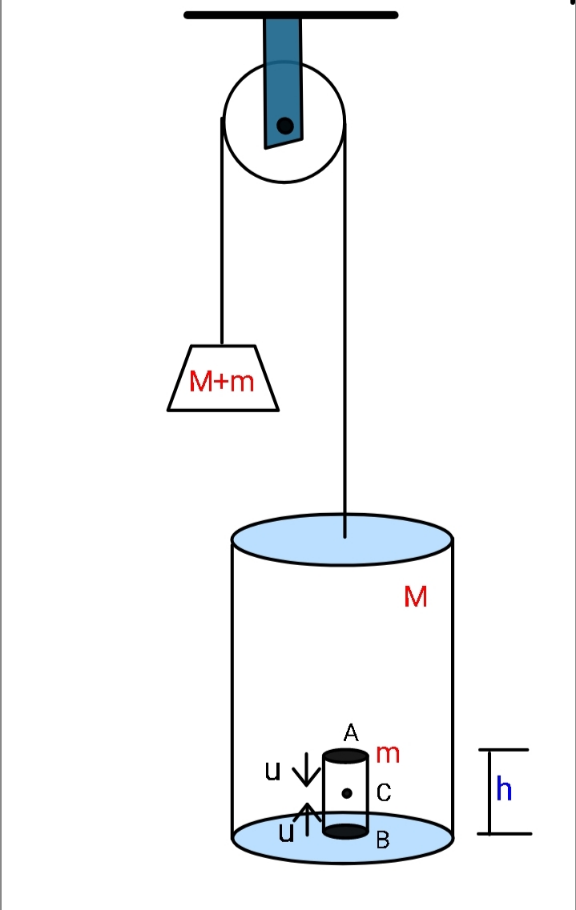
Question Number 153374 by ajfour last updated on 06/Sep/21
Commented by mr W last updated on 06/Sep/21
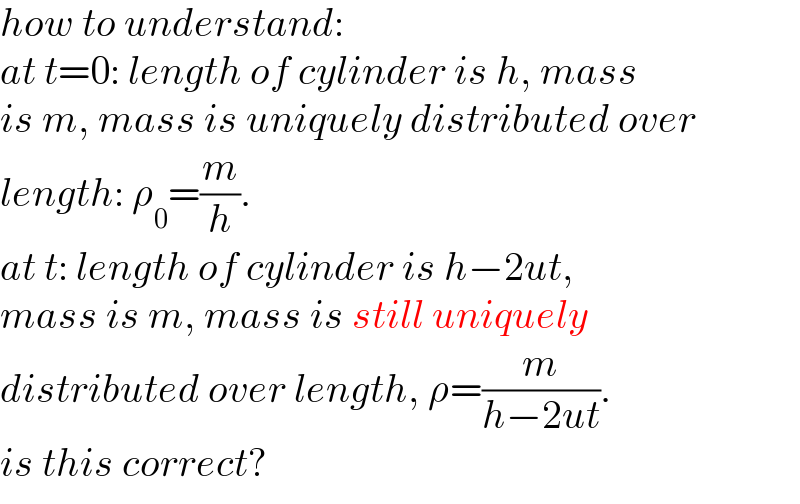
$${how}\:{to}\:{understand}: \\ $$$${at}\:{t}=\mathrm{0}:\:{length}\:{of}\:{cylinder}\:{is}\:{h},\:{mass} \\ $$$${is}\:{m},\:{mass}\:{is}\:{uniquely}\:{distributed}\:{over} \\ $$$${length}:\:\rho_{\mathrm{0}} =\frac{{m}}{{h}}. \\ $$$${at}\:{t}:\:{length}\:{of}\:{cylinder}\:{is}\:{h}−\mathrm{2}{ut}, \\ $$$${mass}\:{is}\:{m},\:{mass}\:{is}\:{still}\:{uniquely} \\ $$$${distributed}\:{over}\:{length},\:\rho=\frac{{m}}{{h}−\mathrm{2}{ut}}. \\ $$$${is}\:{this}\:{correct}? \\ $$
Commented by ajfour last updated on 06/Sep/21
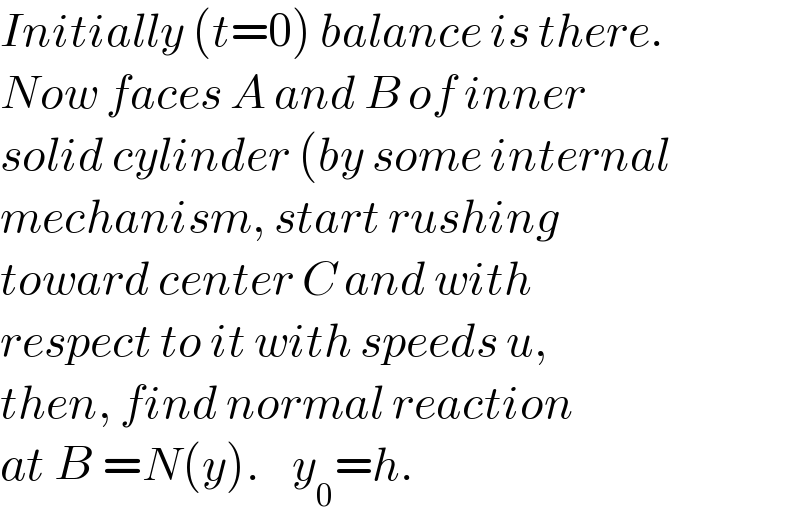
$${Initially}\:\left({t}=\mathrm{0}\right)\:{balance}\:{is}\:{there}. \\ $$$${Now}\:{faces}\:{A}\:{and}\:{B}\:{of}\:{inner} \\ $$$${solid}\:{cylinder}\:\left({by}\:{some}\:{internal}\right. \\ $$$${mechanism},\:{start}\:{rushing} \\ $$$${toward}\:{center}\:{C}\:{and}\:{with}\: \\ $$$${respect}\:{to}\:{it}\:{with}\:{speeds}\:{u}, \\ $$$${then},\:{find}\:{normal}\:{reaction} \\ $$$${at}\:{B}\:={N}\left({y}\right).\:\:\:\:{y}_{\mathrm{0}} ={h}. \\ $$
Commented by ajfour last updated on 06/Sep/21
$${yes}\:{sir},\:{you}\:{get}\:{it}\:{excellent}.. \\ $$
Commented by mr W last updated on 07/Sep/21
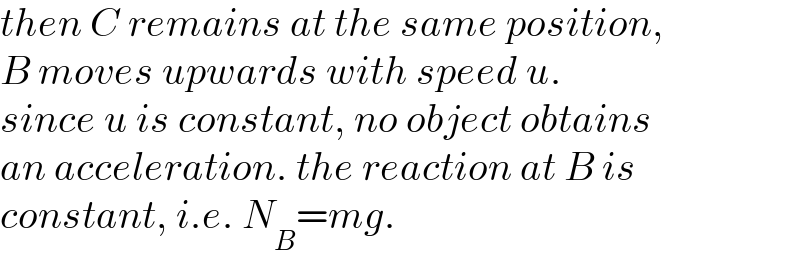
$${then}\:{C}\:{remains}\:{at}\:{the}\:{same}\:{position}, \\ $$$${B}\:{moves}\:{upwards}\:{with}\:{speed}\:{u}. \\ $$$${since}\:{u}\:{is}\:{constant},\:{no}\:{object}\:{obtains} \\ $$$${an}\:{acceleration}.\:{the}\:{reaction}\:{at}\:{B}\:{is} \\ $$$${constant},\:{i}.{e}.\:{N}_{{B}} ={mg}. \\ $$
