Question-153401

Question Number 153401 by rexford last updated on 07/Sep/21

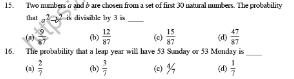
Commented by rexford last updated on 07/Sep/21

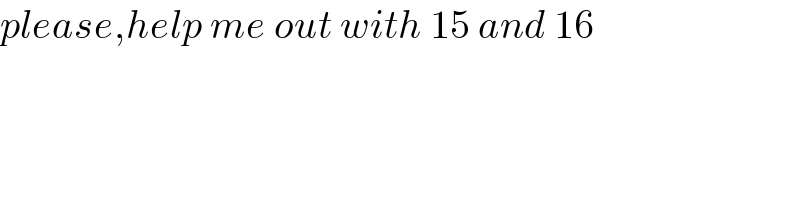
$${please},{help}\:{me}\:{out}\:{with}\:\mathrm{15}\:{and}\:\mathrm{16} \\ $$

Answered by som(math1967) last updated on 07/Sep/21

16. Probability 53 sunday P(A)=(2/7) probability 53 mondayP(B)=(2/7) probability both 53 sunday and monday=P(A)∩P(B)=(1/7) ∴probability 53 sunday or monday P(A)∪P(B)=P(A)+P(B)−P(A)∩P(B) =(2/7)+(2/7) −(1/7)=(3/7) (b)(3/7) ans

$$\mathrm{16}.\:{P}\boldsymbol{{robability}}\:\mathrm{53}\:\boldsymbol{{sunday}}\:\boldsymbol{{P}}\left(\boldsymbol{{A}}\right)=\frac{\mathrm{2}}{\mathrm{7}} \\ $$$$\boldsymbol{{probability}}\:\mathrm{53}\:\boldsymbol{{mondayP}}\left(\boldsymbol{{B}}\right)=\frac{\mathrm{2}}{\mathrm{7}} \\ $$$$\boldsymbol{{probability}}\:\boldsymbol{{both}}\:\mathrm{53}\:\boldsymbol{{sunday}}\:\boldsymbol{{and}} \\ $$$$\boldsymbol{{monday}}=\boldsymbol{{P}}\left(\boldsymbol{{A}}\right)\cap\boldsymbol{{P}}\left(\boldsymbol{{B}}\right)=\frac{\mathrm{1}}{\mathrm{7}} \\ $$$$\therefore\boldsymbol{{probability}}\:\mathrm{53}\:\boldsymbol{{sunday}}\:\boldsymbol{{or}}\:\boldsymbol{{monday}} \\ $$$$\boldsymbol{{P}}\left(\boldsymbol{{A}}\right)\cup\boldsymbol{{P}}\left(\boldsymbol{{B}}\right)=\boldsymbol{{P}}\left(\boldsymbol{{A}}\right)+\boldsymbol{{P}}\left(\boldsymbol{{B}}\right)−\boldsymbol{{P}}\left(\boldsymbol{{A}}\right)\cap\boldsymbol{{P}}\left(\boldsymbol{{B}}\right) \\ $$$$=\frac{\mathrm{2}}{\mathrm{7}}+\frac{\mathrm{2}}{\mathrm{7}}\:−\frac{\mathrm{1}}{\mathrm{7}}=\frac{\mathrm{3}}{\mathrm{7}} \\ $$$$\left(\boldsymbol{{b}}\right)\frac{\mathrm{3}}{\mathrm{7}}\:\boldsymbol{{ans}} \\ $$

Answered by prakash jain last updated on 07/Sep/21

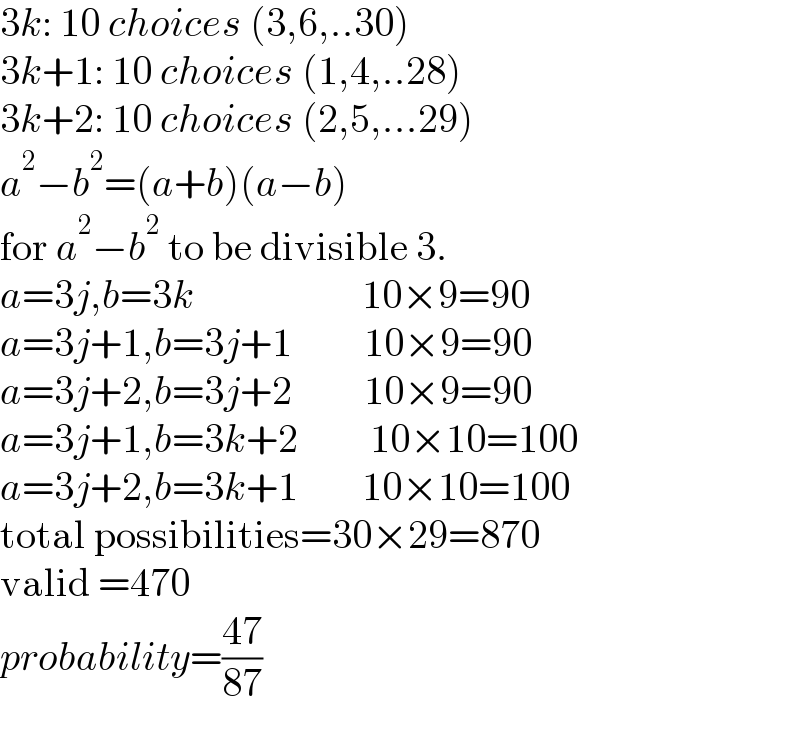
3k: 10 choices (3,6,..30) 3k+1: 10 choices (1,4,..28) 3k+2: 10 choices (2,5,...29) a^2 −b^2 =(a+b)(a−b) for a^2 −b^2 to be divisible 3. a=3j,b=3k 10×9=90 a=3j+1,b=3j+1 10×9=90 a=3j+2,b=3j+2 10×9=90 a=3j+1,b=3k+2 10×10=100 a=3j+2,b=3k+1 10×10=100 total possibilities=30×29=870 valid =470 probability=((47)/(87))

$$\mathrm{3}{k}:\:\mathrm{10}\:{choices}\:\left(\mathrm{3},\mathrm{6},..\mathrm{30}\right) \\ $$$$\mathrm{3}{k}+\mathrm{1}:\:\mathrm{10}\:{choices}\:\left(\mathrm{1},\mathrm{4},..\mathrm{28}\right) \\ $$$$\mathrm{3}{k}+\mathrm{2}:\:\mathrm{10}\:{choices}\:\left(\mathrm{2},\mathrm{5},…\mathrm{29}\right) \\ $$$${a}^{\mathrm{2}} −{b}^{\mathrm{2}} =\left({a}+{b}\right)\left({a}−{b}\right) \\ $$$$\mathrm{for}\:{a}^{\mathrm{2}} −{b}^{\mathrm{2}} \:\mathrm{to}\:\mathrm{be}\:\mathrm{divisible}\:\mathrm{3}. \\ $$$${a}=\mathrm{3}{j},{b}=\mathrm{3}{k}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{10}×\mathrm{9}=\mathrm{90} \\ $$$${a}=\mathrm{3}{j}+\mathrm{1},{b}=\mathrm{3}{j}+\mathrm{1}\:\:\:\:\:\:\:\:\:\mathrm{10}×\mathrm{9}=\mathrm{90} \\ $$$${a}=\mathrm{3}{j}+\mathrm{2},{b}=\mathrm{3}{j}+\mathrm{2}\:\:\:\:\:\:\:\:\:\mathrm{10}×\mathrm{9}=\mathrm{90} \\ $$$${a}=\mathrm{3}{j}+\mathrm{1},{b}=\mathrm{3}{k}+\mathrm{2}\:\:\:\:\:\:\:\:\:\mathrm{10}×\mathrm{10}=\mathrm{100} \\ $$$${a}=\mathrm{3}{j}+\mathrm{2},{b}=\mathrm{3}{k}+\mathrm{1}\:\:\:\:\:\:\:\:\mathrm{10}×\mathrm{10}=\mathrm{100} \\ $$$$\mathrm{total}\:\mathrm{possibilities}=\mathrm{30}×\mathrm{29}=\mathrm{870} \\ $$$$\mathrm{valid}\:=\mathrm{470} \\ $$$${probability}=\frac{\mathrm{47}}{\mathrm{87}} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply