Question-153407

Question Number 153407 by liberty last updated on 07/Sep/21

Answered by Rasheed.Sindhi last updated on 08/Sep/21

x≡2 (mod 5)........(i) x≡1 (mod 3)........(ii) x≡6 (mod 14)......(iii) x≡5 (mod 11).......(iv) _(−_ ) (iii):6,20,34, (iii)&(ii):34,76,118,160,202 (i)&(ii)&(iii):202,412 (i)&(ii)&(iii)&(iv):412

$${x}\equiv\mathrm{2}\:\left({mod}\:\mathrm{5}\right)……..\left({i}\right) \\ $$$${x}\equiv\mathrm{1}\:\left({mod}\:\mathrm{3}\right)……..\left({ii}\right) \\ $$$${x}\equiv\mathrm{6}\:\left({mod}\:\mathrm{14}\right)……\left({iii}\right) \\ $$$$\underset{\underset{} {−}} {{x}\equiv\mathrm{5}\underline{\:\left({mod}\:\mathrm{11}\right)…….\left({iv}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:}\:\:\:\:\:\:\:\:\:}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\:\left({iii}\right):\mathrm{6},\mathrm{20},\mathrm{34}, \\ $$$$\left({iii}\right)\&\left({ii}\right):\mathrm{34},\mathrm{76},\mathrm{118},\mathrm{160},\mathrm{202} \\ $$$$\left({i}\right)\&\left({ii}\right)\&\left({iii}\right):\mathrm{202},\mathrm{412} \\ $$$$\left({i}\right)\&\left({ii}\right)\&\left({iii}\right)\&\left({iv}\right):\mathrm{412} \\ $$

Answered by Rasheed.Sindhi last updated on 13/Sep/21

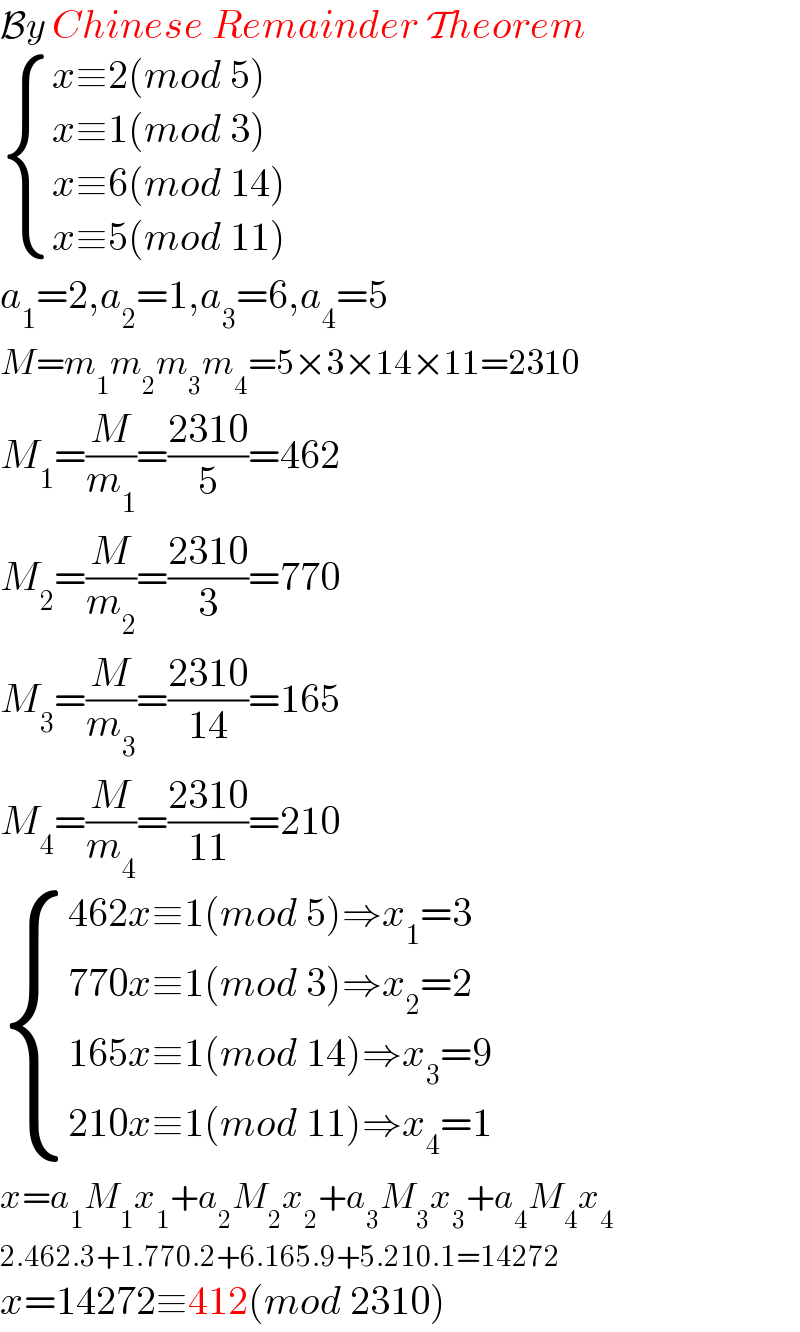
By Chinese Remainder Theorem { ((x≡2(mod 5))),((x≡1(mod 3))),((x≡6(mod 14))),((x≡5(mod 11))) :} a_1 =2,a_2 =1,a_3 =6,a_4 =5 M=m_1 m_2 m_3 m_4 =5×3×14×11=2310 M_1 =(M/m_1 )=((2310)/5)=462 M_2 =(M/m_2 )=((2310)/3)=770 M_3 =(M/m_3 )=((2310)/(14))=165 M_4 =(M/m_4 )=((2310)/(11))=210 { ((462x≡1(mod 5)⇒x_1 =3)),((770x≡1(mod 3)⇒x_2 =2)),((165x≡1(mod 14)⇒x_3 =9)),((210x≡1(mod 11)⇒x_4 =1)) :} x=a_1 M_1 x_1 +a_2 M_2 x_2 +a_3 M_3 x_3 +a_4 M_4 x_4 2.462.3+1.770.2+6.165.9+5.210.1=14272 x=14272≡412(mod 2310)

$$\mathcal{B}{y}\:{Chinese}\:{Remainder}\:\mathcal{T}{heorem} \\ $$$$\begin{cases}{{x}\equiv\mathrm{2}\left({mod}\:\mathrm{5}\right)}\\{{x}\equiv\mathrm{1}\left({mod}\:\mathrm{3}\right)}\\{{x}\equiv\mathrm{6}\left({mod}\:\mathrm{14}\right)}\\{{x}\equiv\mathrm{5}\left({mod}\:\mathrm{11}\right)}\end{cases}\:\:\: \\ $$$${a}_{\mathrm{1}} =\mathrm{2},{a}_{\mathrm{2}} =\mathrm{1},{a}_{\mathrm{3}} =\mathrm{6},{a}_{\mathrm{4}} =\mathrm{5} \\ $$$${M}={m}_{\mathrm{1}} {m}_{\mathrm{2}} {m}_{\mathrm{3}} {m}_{\mathrm{4}} =\mathrm{5}×\mathrm{3}×\mathrm{14}×\mathrm{11}=\mathrm{2310} \\ $$$${M}_{\mathrm{1}} =\frac{{M}}{{m}_{\mathrm{1}} }=\frac{\mathrm{2310}}{\mathrm{5}}=\mathrm{462} \\ $$$${M}_{\mathrm{2}} =\frac{{M}}{{m}_{\mathrm{2}} }=\frac{\mathrm{2310}}{\mathrm{3}}=\mathrm{770} \\ $$$${M}_{\mathrm{3}} =\frac{{M}}{{m}_{\mathrm{3}} }=\frac{\mathrm{2310}}{\mathrm{14}}=\mathrm{165} \\ $$$${M}_{\mathrm{4}} =\frac{{M}}{{m}_{\mathrm{4}} }=\frac{\mathrm{2310}}{\mathrm{11}}=\mathrm{210} \\ $$$$\begin{cases}{\mathrm{462}{x}\equiv\mathrm{1}\left({mod}\:\mathrm{5}\right)\Rightarrow{x}_{\mathrm{1}} =\mathrm{3}}\\{\mathrm{770}{x}\equiv\mathrm{1}\left({mod}\:\mathrm{3}\right)\Rightarrow{x}_{\mathrm{2}} =\mathrm{2}}\\{\mathrm{165}{x}\equiv\mathrm{1}\left({mod}\:\mathrm{14}\right)\Rightarrow{x}_{\mathrm{3}} =\mathrm{9}}\\{\mathrm{210}{x}\equiv\mathrm{1}\left({mod}\:\mathrm{11}\right)\Rightarrow{x}_{\mathrm{4}} =\mathrm{1}}\end{cases} \\ $$$${x}={a}_{\mathrm{1}} {M}_{\mathrm{1}} {x}_{\mathrm{1}} +{a}_{\mathrm{2}} {M}_{\mathrm{2}} {x}_{\mathrm{2}} +{a}_{\mathrm{3}} {M}_{\mathrm{3}} {x}_{\mathrm{3}} +{a}_{\mathrm{4}} {M}_{\mathrm{4}} {x}_{\mathrm{4}} \\ $$$$\mathrm{2}.\mathrm{462}.\mathrm{3}+\mathrm{1}.\mathrm{770}.\mathrm{2}+\mathrm{6}.\mathrm{165}.\mathrm{9}+\mathrm{5}.\mathrm{210}.\mathrm{1}=\mathrm{14272} \\ $$$${x}=\mathrm{14272}\equiv\mathrm{412}\left({mod}\:\mathrm{2310}\right) \\ $$

Commented by liberty last updated on 13/Sep/21

$${yes}… \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply