Question Number 153457 by 0731619 last updated on 07/Sep/21
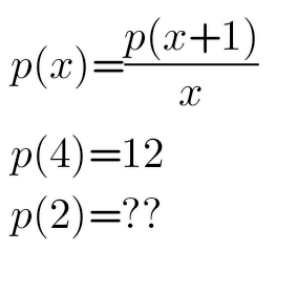
Answered by liberty last updated on 07/Sep/21
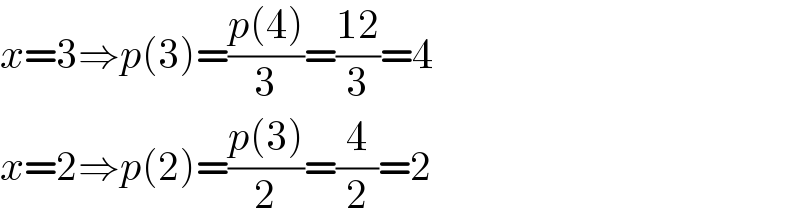
$${x}=\mathrm{3}\Rightarrow{p}\left(\mathrm{3}\right)=\frac{{p}\left(\mathrm{4}\right)}{\mathrm{3}}=\frac{\mathrm{12}}{\mathrm{3}}=\mathrm{4} \\ $$$${x}=\mathrm{2}\Rightarrow{p}\left(\mathrm{2}\right)=\frac{{p}\left(\mathrm{3}\right)}{\mathrm{2}}=\frac{\mathrm{4}}{\mathrm{2}}=\mathrm{2} \\ $$
Answered by Rasheed.Sindhi last updated on 08/Sep/21
![p(x)=((p(x+1))/x) ; p(4)=12 ; p(2)=? p(x)=(( ((p(x+2))/(x+1)) )/x) [∵ p(x+1)=((p(x+2))/(x+1)) ] p(x)=((p(x+2))/(x(x+1))) p(2)=((p(2+2))/(2(2+1)))=((p(4))/(2(3)))=((12)/6)=2](https://www.tinkutara.com/question/Q153492.png)
$${p}\left({x}\right)=\frac{{p}\left({x}+\mathrm{1}\right)}{{x}}\:\:;\:{p}\left(\mathrm{4}\right)=\mathrm{12}\:;\:{p}\left(\mathrm{2}\right)=? \\ $$$${p}\left({x}\right)=\frac{\:\:\frac{{p}\left({x}+\mathrm{2}\right)}{{x}+\mathrm{1}}\:\:}{{x}}\:\:\left[\because\:{p}\left({x}+\mathrm{1}\right)=\frac{{p}\left({x}+\mathrm{2}\right)}{{x}+\mathrm{1}}\:\right] \\ $$$${p}\left({x}\right)=\frac{{p}\left({x}+\mathrm{2}\right)}{{x}\left({x}+\mathrm{1}\right)} \\ $$$${p}\left(\mathrm{2}\right)=\frac{{p}\left(\mathrm{2}+\mathrm{2}\right)}{\mathrm{2}\left(\mathrm{2}+\mathrm{1}\right)}=\frac{{p}\left(\mathrm{4}\right)}{\mathrm{2}\left(\mathrm{3}\right)}=\frac{\mathrm{12}}{\mathrm{6}}=\mathrm{2} \\ $$
