Question Number 153483 by cherokeesay last updated on 07/Sep/21
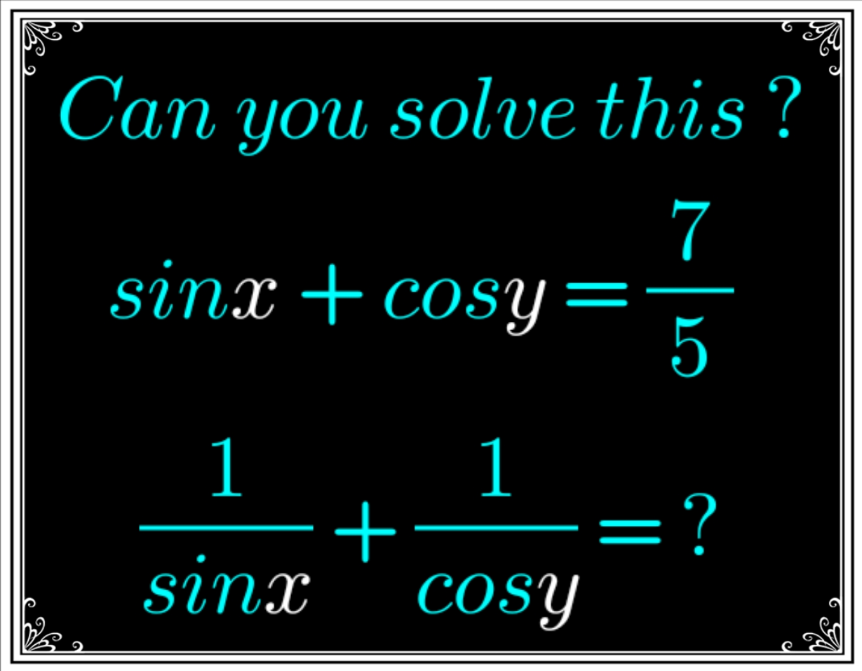
Commented by mr W last updated on 07/Sep/21
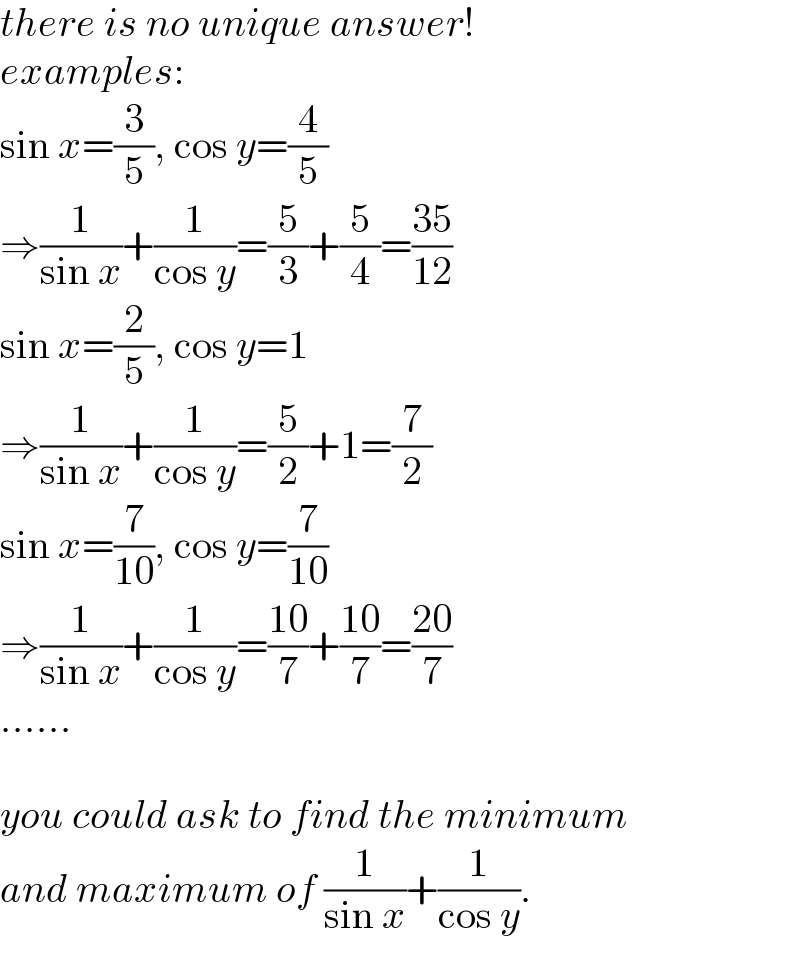
$${there}\:{is}\:{no}\:{unique}\:{answer}! \\ $$$${examples}: \\ $$$$\mathrm{sin}\:{x}=\frac{\mathrm{3}}{\mathrm{5}},\:\mathrm{cos}\:{y}=\frac{\mathrm{4}}{\mathrm{5}}\: \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{sin}\:{x}}+\frac{\mathrm{1}}{\mathrm{cos}\:{y}}=\frac{\mathrm{5}}{\mathrm{3}}+\frac{\mathrm{5}}{\mathrm{4}}=\frac{\mathrm{35}}{\mathrm{12}} \\ $$$$\mathrm{sin}\:{x}=\frac{\mathrm{2}}{\mathrm{5}},\:\mathrm{cos}\:{y}=\mathrm{1} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{sin}\:{x}}+\frac{\mathrm{1}}{\mathrm{cos}\:{y}}=\frac{\mathrm{5}}{\mathrm{2}}+\mathrm{1}=\frac{\mathrm{7}}{\mathrm{2}} \\ $$$$\mathrm{sin}\:{x}=\frac{\mathrm{7}}{\mathrm{10}},\:\mathrm{cos}\:{y}=\frac{\mathrm{7}}{\mathrm{10}} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{sin}\:{x}}+\frac{\mathrm{1}}{\mathrm{cos}\:{y}}=\frac{\mathrm{10}}{\mathrm{7}}+\frac{\mathrm{10}}{\mathrm{7}}=\frac{\mathrm{20}}{\mathrm{7}} \\ $$$$…… \\ $$$$ \\ $$$${you}\:{could}\:{ask}\:{to}\:{find}\:{the}\:{minimum} \\ $$$${and}\:{maximum}\:{of}\:\frac{\mathrm{1}}{\mathrm{sin}\:{x}}+\frac{\mathrm{1}}{\mathrm{cos}\:{y}}. \\ $$
Commented by mr W last updated on 07/Sep/21
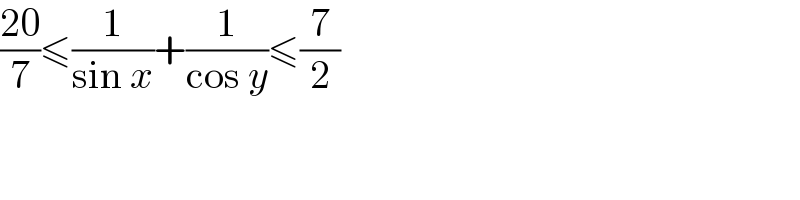
$$\frac{\mathrm{20}}{\mathrm{7}}\leqslant\frac{\mathrm{1}}{\mathrm{sin}\:{x}}+\frac{\mathrm{1}}{\mathrm{cos}\:{y}}\leqslant\frac{\mathrm{7}}{\mathrm{2}} \\ $$
Commented by yeti123 last updated on 08/Sep/21
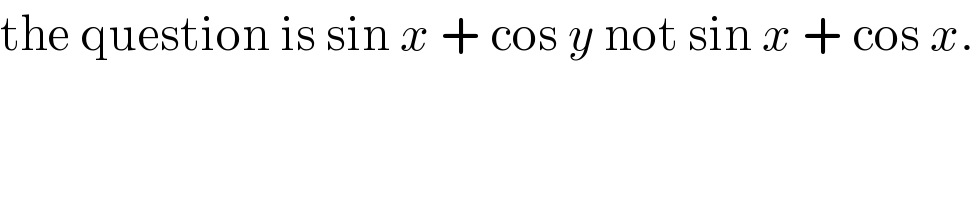
$$\mathrm{the}\:\mathrm{question}\:\mathrm{is}\:\mathrm{sin}\:{x}\:+\:\mathrm{cos}\:{y}\:\mathrm{not}\:\mathrm{sin}\:{x}\:+\:\mathrm{cos}\:{x}. \\ $$
Commented by cherokeesay last updated on 08/Sep/21

$${my}\:{solution}\:: \\ $$$$\left({sinx}\:+\:{cosx}\right)^{\mathrm{2}} \:=\:\frac{\mathrm{49}}{\mathrm{25}}\:\Leftrightarrow\: \\ $$$${sin}^{\mathrm{2}} {x}\:+\:{cos}^{\mathrm{2}} {x}\:+\:\mathrm{2}{sinxcosx}\:=\:\frac{\mathrm{49}}{\mathrm{25}}\:\Rightarrow\: \\ $$$$\mathrm{2}{sinxcosx}=\:{sin}\mathrm{2}{x}\:=\:\frac{\mathrm{49}}{\mathrm{25}}\:−\:\mathrm{1}\:=\:\frac{\mathrm{24}}{\mathrm{25}} \\ $$$$\frac{\mathrm{1}}{{sinx}}\:+\:\frac{\mathrm{1}}{{cosx}}\:=\:\frac{{sinx}\:+\:{cosy}}{{sinxcosx}}\:= \\ $$$$\frac{\frac{\mathrm{7}}{\mathrm{5}}}{\frac{\mathrm{1}}{\mathrm{2}}{sin}\mathrm{2}{x}}\:=\:\frac{\frac{\mathrm{7}}{\mathrm{5}}}{\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{24}}{\mathrm{25}}}\:=\:\frac{\frac{\mathrm{7}}{\mathrm{5}}}{\frac{\mathrm{12}}{\mathrm{25}}}\:=\:\frac{\mathrm{7}}{\mathrm{5}}×\frac{\mathrm{25}}{\mathrm{12}}\:=\:\frac{\mathrm{35}}{\mathrm{12}} \\ $$$$ \\ $$
Commented by liberty last updated on 08/Sep/21
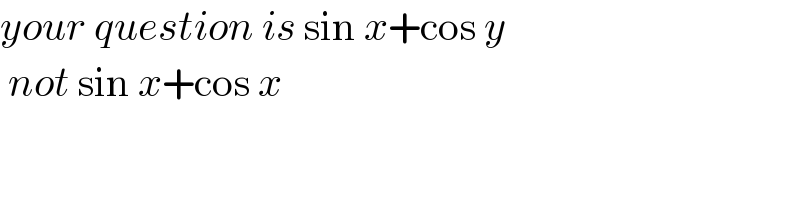
$${your}\:{question}\:{is}\:\mathrm{sin}\:{x}+\mathrm{cos}\:{y}\: \\ $$$$\:{not}\:\mathrm{sin}\:{x}+\mathrm{cos}\:{x}\: \\ $$
Commented by cherokeesay last updated on 08/Sep/21

$${error}\:{that}\:{I}\:{just}\:{rectfied}. \\ $$$${thank}\:{you} \\ $$
Answered by ybav last updated on 07/Sep/21

$${i}\:{think}\:{its}\:\mathrm{25}/\mathrm{49} \\ $$
Answered by maged last updated on 08/Sep/21
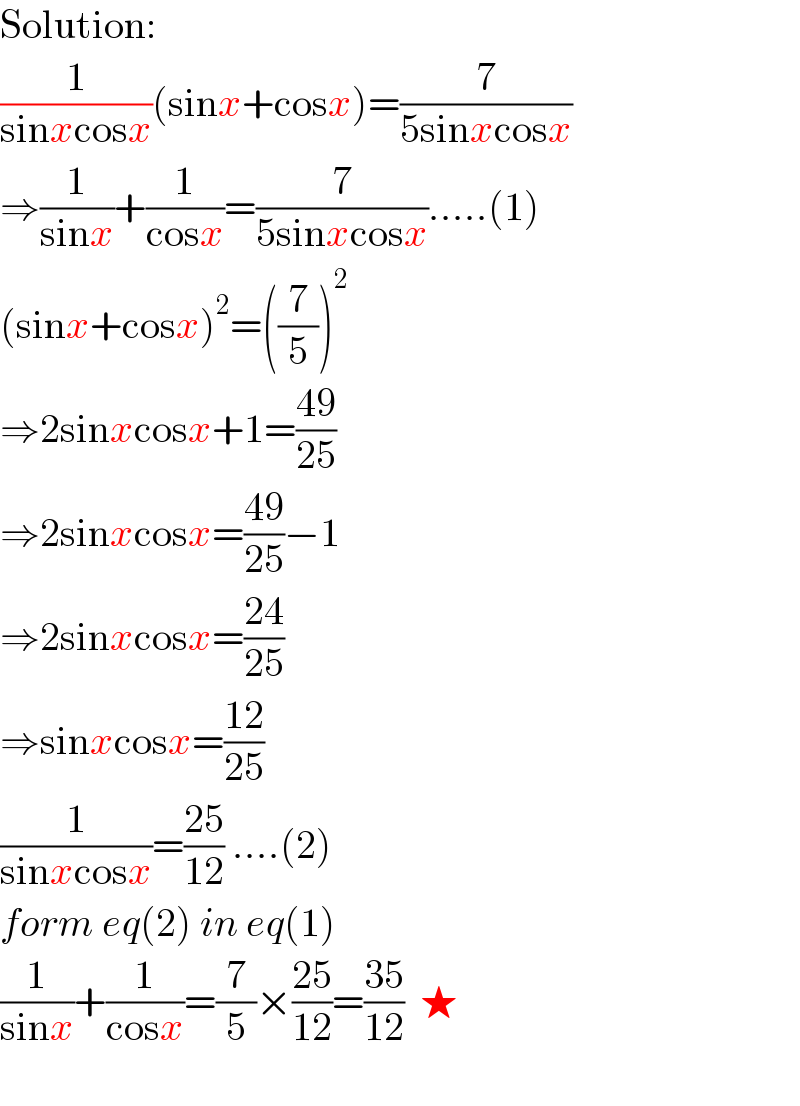
$$\mathrm{Solution}: \\ $$$$\frac{\mathrm{1}}{\mathrm{sin}{x}\mathrm{cos}{x}}\left(\mathrm{sin}{x}+\mathrm{cos}{x}\right)=\frac{\mathrm{7}}{\mathrm{5sin}{x}\mathrm{cos}{x}} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{sin}{x}}+\frac{\mathrm{1}}{\mathrm{cos}{x}}=\frac{\mathrm{7}}{\mathrm{5sin}{x}\mathrm{cos}{x}}…..\left(\mathrm{1}\right) \\ $$$$\left(\mathrm{sin}{x}+\mathrm{cos}{x}\right)^{\mathrm{2}} =\left(\frac{\mathrm{7}}{\mathrm{5}}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{2sin}{x}\mathrm{cos}{x}+\mathrm{1}=\frac{\mathrm{49}}{\mathrm{25}} \\ $$$$\Rightarrow\mathrm{2sin}{x}\mathrm{cos}{x}=\frac{\mathrm{49}}{\mathrm{25}}−\mathrm{1} \\ $$$$\Rightarrow\mathrm{2sin}{x}\mathrm{cos}{x}=\frac{\mathrm{24}}{\mathrm{25}} \\ $$$$\Rightarrow\mathrm{sin}{x}\mathrm{cos}{x}=\frac{\mathrm{12}}{\mathrm{25}} \\ $$$$\frac{\mathrm{1}}{\mathrm{sin}{x}\mathrm{cos}{x}}=\frac{\mathrm{25}}{\mathrm{12}}\:….\left(\mathrm{2}\right) \\ $$$${form}\:{eq}\left(\mathrm{2}\right)\:{in}\:{eq}\left(\mathrm{1}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{sin}{x}}+\frac{\mathrm{1}}{\mathrm{cos}{x}}=\frac{\mathrm{7}}{\mathrm{5}}×\frac{\mathrm{25}}{\mathrm{12}}=\frac{\mathrm{35}}{\mathrm{12}}\:\:\bigstar \\ $$$$ \\ $$
Commented by yeti123 last updated on 08/Sep/21
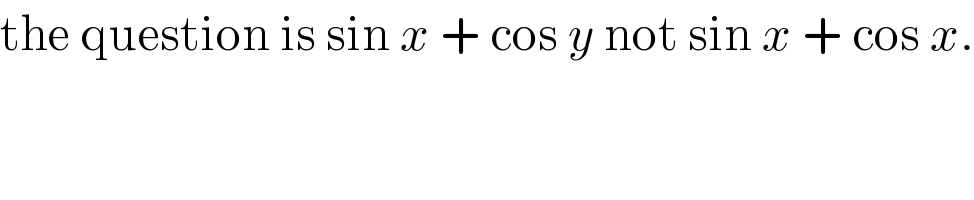
$$\mathrm{the}\:\mathrm{question}\:\mathrm{is}\:\mathrm{sin}\:{x}\:+\:\mathrm{cos}\:{y}\:\mathrm{not}\:\mathrm{sin}\:{x}\:+\:\mathrm{cos}\:{x}. \\ $$
Commented by liberty last updated on 08/Sep/21
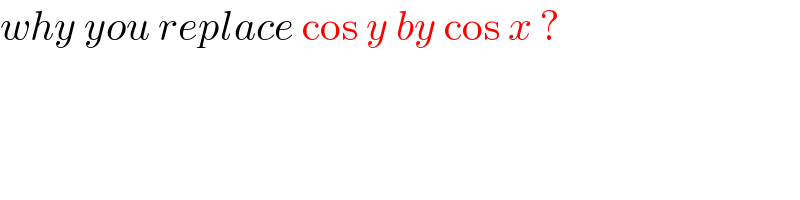
$${why}\:{you}\:{replace}\:\mathrm{cos}\:{y}\:{by}\:\mathrm{cos}\:{x}\:? \\ $$
Commented by cherokeesay last updated on 08/Sep/21

$${error}\:{that}\:{I}\:{just}\:{rectified}= \\ $$$${thanks} \\ $$
