Question Number 153505 by mathdanisur last updated on 07/Sep/21

Commented by MJS_new last updated on 08/Sep/21
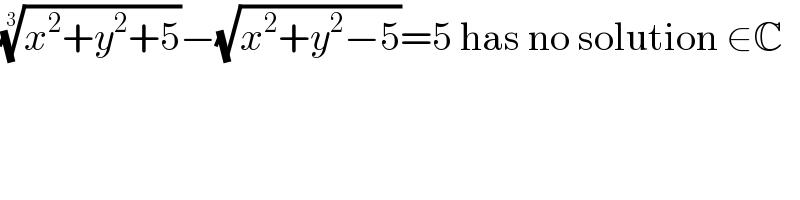
$$\sqrt[{\mathrm{3}}]{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{5}}−\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{5}}=\mathrm{5}\:\mathrm{has}\:\mathrm{no}\:\mathrm{solution}\:\in\mathbb{C} \\ $$
Answered by liberty last updated on 08/Sep/21
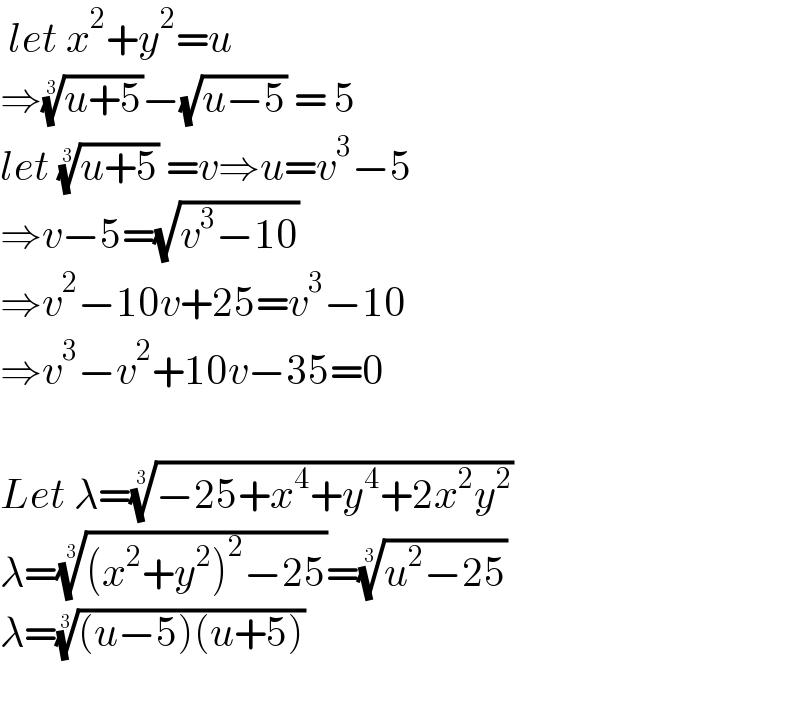
$$\:{let}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} ={u} \\ $$$$\Rightarrow\sqrt[{\mathrm{3}}]{{u}+\mathrm{5}}−\sqrt{{u}−\mathrm{5}}\:=\:\mathrm{5} \\ $$$${let}\:\sqrt[{\mathrm{3}}]{{u}+\mathrm{5}}\:={v}\Rightarrow{u}={v}^{\mathrm{3}} −\mathrm{5} \\ $$$$\Rightarrow{v}−\mathrm{5}=\sqrt{{v}^{\mathrm{3}} −\mathrm{10}} \\ $$$$\Rightarrow{v}^{\mathrm{2}} −\mathrm{10}{v}+\mathrm{25}={v}^{\mathrm{3}} −\mathrm{10} \\ $$$$\Rightarrow{v}^{\mathrm{3}} −{v}^{\mathrm{2}} +\mathrm{10}{v}−\mathrm{35}=\mathrm{0} \\ $$$$ \\ $$$${Let}\:\lambda=\sqrt[{\mathrm{3}}]{−\mathrm{25}+{x}^{\mathrm{4}} +{y}^{\mathrm{4}} +\mathrm{2}{x}^{\mathrm{2}} {y}^{\mathrm{2}} } \\ $$$$\lambda=\sqrt[{\mathrm{3}}]{\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{25}}=\sqrt[{\mathrm{3}}]{{u}^{\mathrm{2}} −\mathrm{25}} \\ $$$$\lambda=\sqrt[{\mathrm{3}}]{\left({u}−\mathrm{5}\right)\left({u}+\mathrm{5}\right)}\: \\ $$$$ \\ $$
Commented by mr W last updated on 08/Sep/21
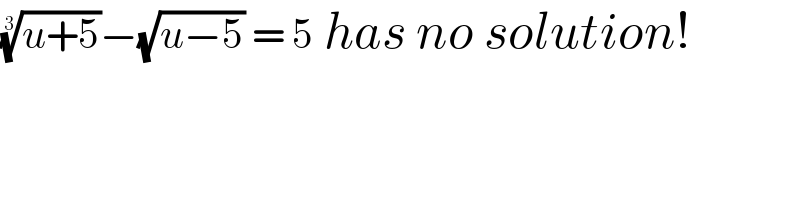
$$\sqrt[{\mathrm{3}}]{{u}+\mathrm{5}}−\sqrt{{u}−\mathrm{5}}\:=\:\mathrm{5}\:{has}\:{no}\:{solution}! \\ $$
