Question Number 153638 by mathdanisur last updated on 08/Sep/21
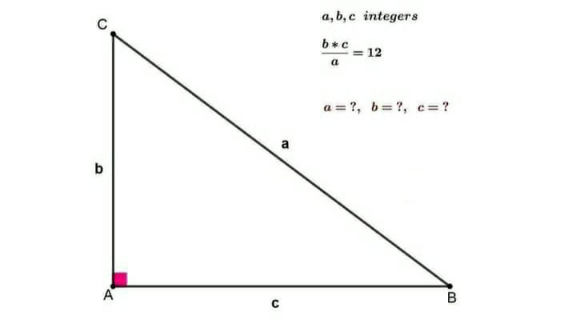
Commented by EDWIN88 last updated on 09/Sep/21
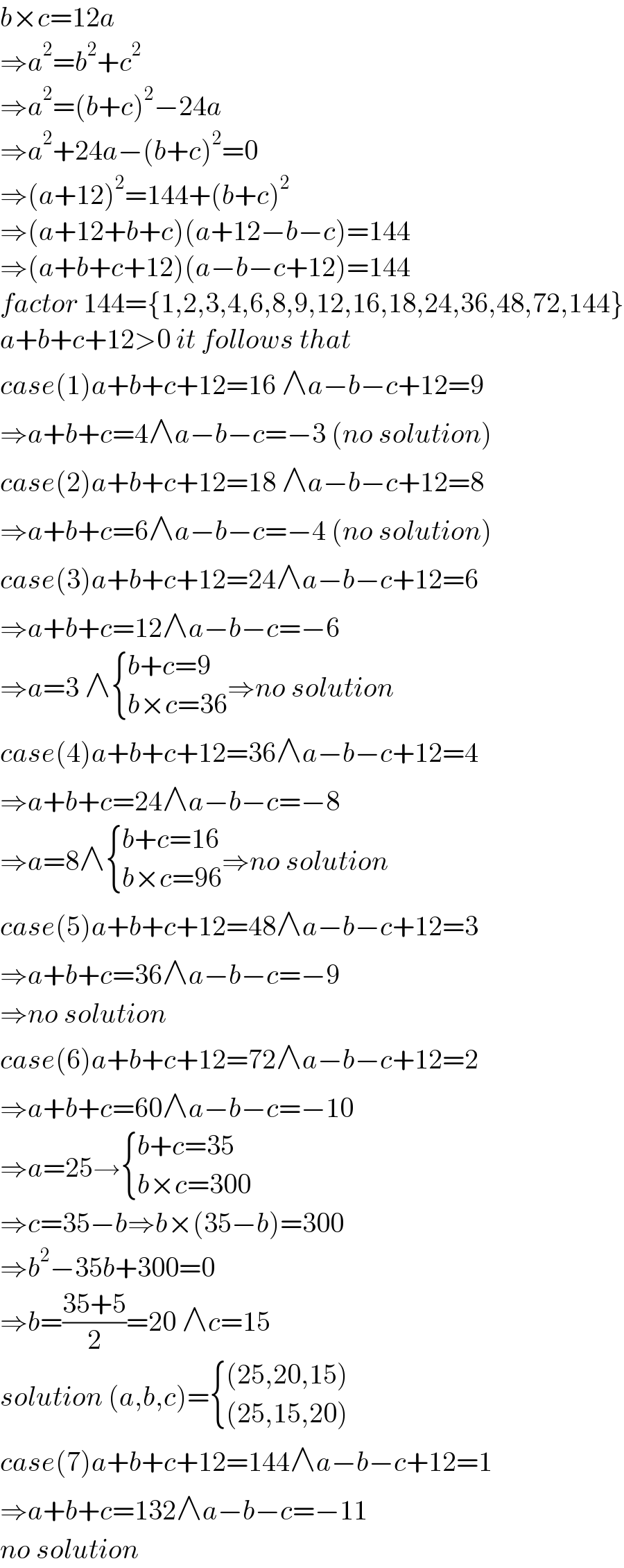
$${b}×{c}=\mathrm{12}{a} \\ $$$$\Rightarrow{a}^{\mathrm{2}} ={b}^{\mathrm{2}} +{c}^{\mathrm{2}} \\ $$$$\Rightarrow{a}^{\mathrm{2}} =\left({b}+{c}\right)^{\mathrm{2}} −\mathrm{24}{a} \\ $$$$\Rightarrow{a}^{\mathrm{2}} +\mathrm{24}{a}−\left({b}+{c}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow\left({a}+\mathrm{12}\right)^{\mathrm{2}} =\mathrm{144}+\left({b}+{c}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\left({a}+\mathrm{12}+{b}+{c}\right)\left({a}+\mathrm{12}−{b}−{c}\right)=\mathrm{144} \\ $$$$\Rightarrow\left({a}+{b}+{c}+\mathrm{12}\right)\left({a}−{b}−{c}+\mathrm{12}\right)=\mathrm{144} \\ $$$${factor}\:\mathrm{144}=\left\{\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4},\mathrm{6},\mathrm{8},\mathrm{9},\mathrm{12},\mathrm{16},\mathrm{18},\mathrm{24},\mathrm{36},\mathrm{48},\mathrm{72},\mathrm{144}\right\} \\ $$$${a}+{b}+{c}+\mathrm{12}>\mathrm{0}\:{it}\:{follows}\:{that} \\ $$$${case}\left(\mathrm{1}\right){a}+{b}+{c}+\mathrm{12}=\mathrm{16}\:\wedge{a}−{b}−{c}+\mathrm{12}=\mathrm{9} \\ $$$$\Rightarrow{a}+{b}+{c}=\mathrm{4}\wedge{a}−{b}−{c}=−\mathrm{3}\:\left({no}\:{solution}\right) \\ $$$${case}\left(\mathrm{2}\right){a}+{b}+{c}+\mathrm{12}=\mathrm{18}\:\wedge{a}−{b}−{c}+\mathrm{12}=\mathrm{8} \\ $$$$\Rightarrow{a}+{b}+{c}=\mathrm{6}\wedge{a}−{b}−{c}=−\mathrm{4}\:\left({no}\:{solution}\right) \\ $$$${case}\left(\mathrm{3}\right){a}+{b}+{c}+\mathrm{12}=\mathrm{24}\wedge{a}−{b}−{c}+\mathrm{12}=\mathrm{6} \\ $$$$\Rightarrow{a}+{b}+{c}=\mathrm{12}\wedge{a}−{b}−{c}=−\mathrm{6} \\ $$$$\Rightarrow{a}=\mathrm{3}\:\wedge\begin{cases}{{b}+{c}=\mathrm{9}}\\{{b}×{c}=\mathrm{36}}\end{cases}\Rightarrow{no}\:{solution} \\ $$$${case}\left(\mathrm{4}\right){a}+{b}+{c}+\mathrm{12}=\mathrm{36}\wedge{a}−{b}−{c}+\mathrm{12}=\mathrm{4} \\ $$$$\Rightarrow{a}+{b}+{c}=\mathrm{24}\wedge{a}−{b}−{c}=−\mathrm{8} \\ $$$$\Rightarrow{a}=\mathrm{8}\wedge\begin{cases}{{b}+{c}=\mathrm{16}}\\{{b}×{c}=\mathrm{96}}\end{cases}\Rightarrow{no}\:{solution} \\ $$$${case}\left(\mathrm{5}\right){a}+{b}+{c}+\mathrm{12}=\mathrm{48}\wedge{a}−{b}−{c}+\mathrm{12}=\mathrm{3} \\ $$$$\Rightarrow{a}+{b}+{c}=\mathrm{36}\wedge{a}−{b}−{c}=−\mathrm{9} \\ $$$$\Rightarrow{no}\:{solution} \\ $$$${case}\left(\mathrm{6}\right){a}+{b}+{c}+\mathrm{12}=\mathrm{72}\wedge{a}−{b}−{c}+\mathrm{12}=\mathrm{2} \\ $$$$\Rightarrow{a}+{b}+{c}=\mathrm{60}\wedge{a}−{b}−{c}=−\mathrm{10} \\ $$$$\Rightarrow{a}=\mathrm{25}\rightarrow\begin{cases}{{b}+{c}=\mathrm{35}}\\{{b}×{c}=\mathrm{300}}\end{cases} \\ $$$$\Rightarrow{c}=\mathrm{35}−{b}\Rightarrow{b}×\left(\mathrm{35}−{b}\right)=\mathrm{300} \\ $$$$\Rightarrow{b}^{\mathrm{2}} −\mathrm{35}{b}+\mathrm{300}=\mathrm{0} \\ $$$$\Rightarrow{b}=\frac{\mathrm{35}+\mathrm{5}}{\mathrm{2}}=\mathrm{20}\:\wedge{c}=\mathrm{15} \\ $$$${solution}\:\left({a},{b},{c}\right)=\begin{cases}{\left(\mathrm{25},\mathrm{20},\mathrm{15}\right)}\\{\left(\mathrm{25},\mathrm{15},\mathrm{20}\right)}\end{cases} \\ $$$${case}\left(\mathrm{7}\right){a}+{b}+{c}+\mathrm{12}=\mathrm{144}\wedge{a}−{b}−{c}+\mathrm{12}=\mathrm{1} \\ $$$$\Rightarrow{a}+{b}+{c}=\mathrm{132}\wedge{a}−{b}−{c}=−\mathrm{11} \\ $$$${no}\:{solution} \\ $$
Commented by mathdanisur last updated on 11/Sep/21

$$\mathrm{thanks}\:\mathrm{ser}\:\mathrm{nice} \\ $$
Answered by MJS_new last updated on 09/Sep/21
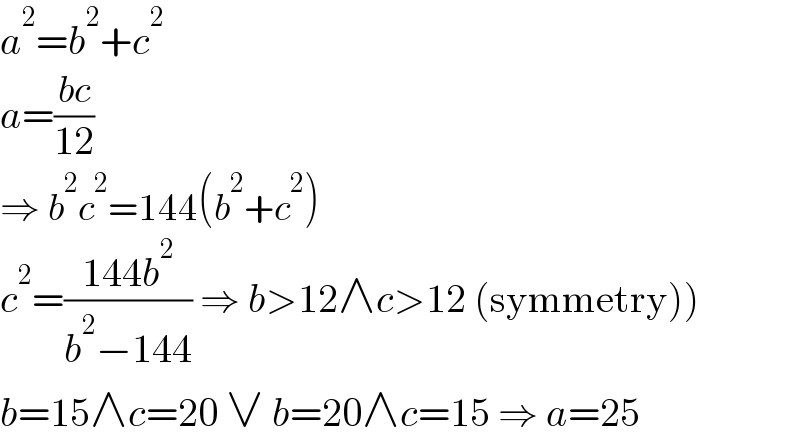
$${a}^{\mathrm{2}} ={b}^{\mathrm{2}} +{c}^{\mathrm{2}} \\ $$$${a}=\frac{{bc}}{\mathrm{12}} \\ $$$$\Rightarrow\:{b}^{\mathrm{2}} {c}^{\mathrm{2}} =\mathrm{144}\left({b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right) \\ $$$$\left.{c}^{\mathrm{2}} =\frac{\mathrm{144}{b}^{\mathrm{2}} }{{b}^{\mathrm{2}} −\mathrm{144}}\:\Rightarrow\:{b}>\mathrm{12}\wedge{c}>\mathrm{12}\:\left(\mathrm{symmetry}\right)\right) \\ $$$${b}=\mathrm{15}\wedge{c}=\mathrm{20}\:\vee\:{b}=\mathrm{20}\wedge{c}=\mathrm{15}\:\Rightarrow\:{a}=\mathrm{25} \\ $$
Commented by Rasheed.Sindhi last updated on 09/Sep/21
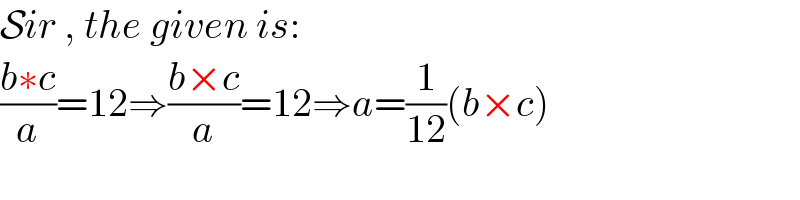
$$\mathcal{S}{ir}\:,\:{the}\:{given}\:{is}: \\ $$$$\frac{{b}\ast{c}}{{a}}=\mathrm{12}\Rightarrow\frac{{b}×{c}}{{a}}=\mathrm{12}\Rightarrow{a}=\frac{\mathrm{1}}{\mathrm{12}}\left({b}×{c}\right) \\ $$
Commented by MJS_new last updated on 09/Sep/21

$$\mathrm{ok}.\:\mathrm{my}\:\mathrm{eyes}… \\ $$
Commented by MJS_new last updated on 09/Sep/21
$$\mathrm{corrected}\:\mathrm{my}\:\mathrm{post}.\:\mathrm{thank}\:\mathrm{you}! \\ $$
