Question Number 153676 by SANOGO last updated on 09/Sep/21
Answered by som(math1967) last updated on 09/Sep/21
![1. a>0,b>0 (a−b)^2 ≥0 [if a=b then(a−b)=0] ⇒(a+b)^2 −4ab≥0 ⇒ (((a+b)/2))^2 ≥ab ∴((a+b)/2)≥(√(ab))](https://www.tinkutara.com/question/Q153680.png)
$$\mathrm{1}.\:\boldsymbol{{a}}>\mathrm{0},\boldsymbol{{b}}>\mathrm{0} \\ $$$$\:\left(\boldsymbol{{a}}−\boldsymbol{{b}}\right)^{\mathrm{2}} \geqslant\mathrm{0}\:\:\:\left[\boldsymbol{{if}}\:\boldsymbol{{a}}=\boldsymbol{{b}}\:\boldsymbol{{then}}\left(\boldsymbol{{a}}−\boldsymbol{{b}}\right)=\mathrm{0}\right] \\ $$$$\Rightarrow\left(\boldsymbol{{a}}+\boldsymbol{{b}}\right)^{\mathrm{2}} −\mathrm{4}\boldsymbol{{ab}}\geqslant\mathrm{0} \\ $$$$\Rightarrow\:\left(\frac{\boldsymbol{{a}}+\boldsymbol{{b}}}{\mathrm{2}}\right)^{\mathrm{2}} \geqslant\boldsymbol{{ab}} \\ $$$$\therefore\frac{\boldsymbol{{a}}+\boldsymbol{{b}}}{\mathrm{2}}\geqslant\sqrt{\boldsymbol{{ab}}} \\ $$
Commented by SANOGO last updated on 09/Sep/21

$${bien}/{mais}\:{stp}\:{quel}\:{est}\:{le}\:{superieur}\:{et}\:{l}'{inferieur} \\ $$
Commented by som(math1967) last updated on 09/Sep/21

$${je}\:{ne}\:{connais}\:{pas}\:{le}\:{francais} \\ $$
Answered by puissant last updated on 11/Sep/21
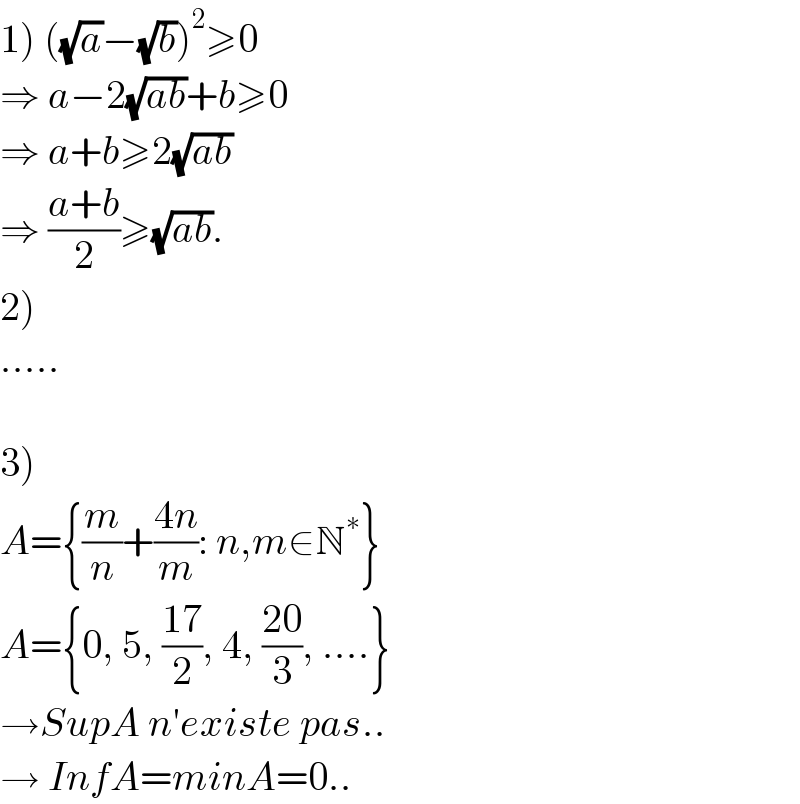
$$\left.\mathrm{1}\right)\:\left(\sqrt{{a}}−\sqrt{{b}}\right)^{\mathrm{2}} \geqslant\mathrm{0} \\ $$$$\Rightarrow\:{a}−\mathrm{2}\sqrt{{ab}}+{b}\geqslant\mathrm{0} \\ $$$$\Rightarrow\:{a}+{b}\geqslant\mathrm{2}\sqrt{{ab}} \\ $$$$\Rightarrow\:\frac{{a}+{b}}{\mathrm{2}}\geqslant\sqrt{{ab}}. \\ $$$$\left.\mathrm{2}\right) \\ $$$$….. \\ $$$$ \\ $$$$\left.\mathrm{3}\right) \\ $$$${A}=\left\{\frac{{m}}{{n}}+\frac{\mathrm{4}{n}}{{m}}:\:{n},{m}\in\mathbb{N}^{\ast} \right\} \\ $$$${A}=\left\{\mathrm{0},\:\mathrm{5},\:\frac{\mathrm{17}}{\mathrm{2}},\:\mathrm{4},\:\frac{\mathrm{20}}{\mathrm{3}},\:….\right\} \\ $$$$\rightarrow{SupA}\:{n}'{existe}\:{pas}.. \\ $$$$\rightarrow\:{InfA}={minA}=\mathrm{0}.. \\ $$
Commented by SANOGO last updated on 09/Sep/21
$${ok}\:{merci}\:{bien}\:{le}\:{tout}\:{puissant} \\ $$
