Menu Close

Question-153685

Tinku Tara 0 Comments
Pin




Question Number 153685 by roxceefocus last updated on 09/Sep/21
Commented by liberty last updated on 09/Sep/21
f(x)=2x^3 +5x^2 +7x+11 divided by x^2 +5x+1 By Horner determinant ((•,2,5,7,(11)),((−5),•,(−10),(−2),•),((−1),•,•,(25),5),(•,2,(−5),(30),(16))) the quotient = 2x−5 the remainder=30x+16 ......correct....
$${f}\left({x}\right)=\mathrm{2}{x}^{\mathrm{3}} +\mathrm{5}{x}^{\mathrm{2}} +\mathrm{7}{x}+\mathrm{11} \\ $$$${divided}\:{by}\:{x}^{\mathrm{2}} +\mathrm{5}{x}+\mathrm{1} \\ $$$${By}\:{Horner} \\ $$$$\:\begin{array}{|c|c|c|c|}{\bullet}&\hline{\mathrm{2}}&\hline{\mathrm{5}}&\hline{\mathrm{7}}&\hline{\mathrm{11}}\\{−\mathrm{5}}&\hline{\bullet}&\hline{−\mathrm{10}}&\hline{−\mathrm{2}}&\hline{\bullet}\\{−\mathrm{1}}&\hline{\bullet}&\hline{\bullet}&\hline{\mathrm{25}}&\hline{\mathrm{5}}\\{\bullet}&\hline{\mathrm{2}}&\hline{−\mathrm{5}}&\hline{\mathrm{30}}&\hline{\mathrm{16}}\\\hline\end{array} \\ $$$${the}\:{quotient}\:=\:\mathrm{2}{x}−\mathrm{5} \\ $$$${the}\:{remainder}=\mathrm{30}{x}+\mathrm{16} \\ $$$$\:\:\:……{correct}…. \\ $$
Commented by roxceefocus last updated on 09/Sep/21
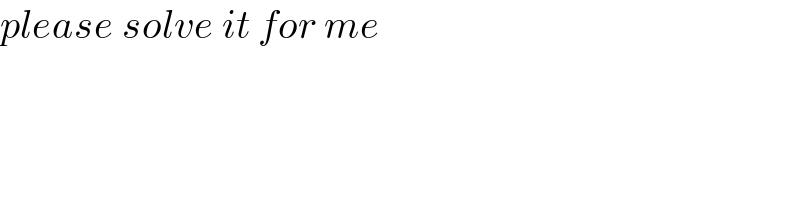
please solve it for me
$${please}\:{solve}\:{it}\:{for}\:{me} \\ $$
Answered by liberty last updated on 09/Sep/21
f(x):x^2 +5x+1 ⇒ { ((the quotient=2x−5)),((the remainder=30x+16)) :} determinant ((,2,( m),( n),( 11)),((−5),•,(−10),( −2),),((−1),•,( •),(−5m+50),(−m+10)),(,2,(m−10),(−5m+n+48),(−m+21))) the quotient ⇒2x+(m−10)≡2x−5 m=5 the remainder ⇒30x+16≡(−5m+n+48)x−m+21 ⇒30=−5×5+n+48 ⇒55−48=n; n=7
$${f}\left({x}\right):{x}^{\mathrm{2}} +\mathrm{5}{x}+\mathrm{1}\:\Rightarrow\begin{cases}{{the}\:{quotient}=\mathrm{2}{x}−\mathrm{5}}\\{{the}\:{remainder}=\mathrm{30}{x}+\mathrm{16}}\end{cases} \\ $$$$\:\begin{array}{|c|c|c|c|}{}&\hline{\mathrm{2}}&\hline{\:\:\:\:{m}}&\hline{\:\:\:\:\:\:\:\:\:\:\:{n}}&\hline{\:\:\:\:\:\mathrm{11}}\\{−\mathrm{5}}&\hline{\bullet}&\hline{−\mathrm{10}}&\hline{\:\:\:\:\:\:\:\:−\mathrm{2}}&\hline{}\\{−\mathrm{1}}&\hline{\bullet}&\hline{\:\:\:\:\bullet}&\hline{−\mathrm{5}{m}+\mathrm{50}}&\hline{−{m}+\mathrm{10}}\\{}&\hline{\mathrm{2}}&\hline{{m}−\mathrm{10}}&\hline{−\mathrm{5}{m}+{n}+\mathrm{48}}&\hline{−{m}+\mathrm{21}}\\\hline\end{array} \\ $$$$\:{the}\:{quotient}\:\Rightarrow\mathrm{2}{x}+\left({m}−\mathrm{10}\right)\equiv\mathrm{2}{x}−\mathrm{5} \\ $$$$\:{m}=\mathrm{5}\: \\ $$$${the}\:{remainder}\:\Rightarrow\mathrm{30}{x}+\mathrm{16}\equiv\left(−\mathrm{5}{m}+{n}+\mathrm{48}\right){x}−{m}+\mathrm{21} \\ $$$$\Rightarrow\mathrm{30}=−\mathrm{5}×\mathrm{5}+{n}+\mathrm{48} \\ $$$$\Rightarrow\mathrm{55}−\mathrm{48}={n};\:{n}=\mathrm{7} \\ $$$$ \\ $$
Commented by Tawa11 last updated on 09/Sep/21
weldone sirs
$$\mathrm{weldone}\:\mathrm{sirs} \\ $$
Answered by Rasheed.Sindhi last updated on 09/Sep/21
f(x)=2x^3 +mx^2 +nx+11........A D(x)=x^2 +5x+1 Q(x)=2x−5 R(x)=30x+16 f(x)=D(x).Q(x)+R(x) =(x^2 +5x+1)(2x−5)+(30x+16) =2x^3 +10x^2 +2x−5x^2 −25x−5+30x+16 =2x^3 +5x^2 +7x+11..............B Comparing coefficients of A &B m=5 & n=7
$${f}\left({x}\right)=\mathrm{2}{x}^{\mathrm{3}} +{mx}^{\mathrm{2}} +{nx}+\mathrm{11}……..{A} \\ $$$${D}\left({x}\right)={x}^{\mathrm{2}} +\mathrm{5}{x}+\mathrm{1} \\ $$$${Q}\left({x}\right)=\mathrm{2}{x}−\mathrm{5} \\ $$$${R}\left({x}\right)=\mathrm{30}{x}+\mathrm{16} \\ $$$${f}\left({x}\right)={D}\left({x}\right).{Q}\left({x}\right)+{R}\left({x}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:=\left({x}^{\mathrm{2}} +\mathrm{5}{x}+\mathrm{1}\right)\left(\mathrm{2}{x}−\mathrm{5}\right)+\left(\mathrm{30}{x}+\mathrm{16}\right) \\ $$$$=\mathrm{2}{x}^{\mathrm{3}} +\mathrm{10}{x}^{\mathrm{2}} +\mathrm{2}{x}−\mathrm{5}{x}^{\mathrm{2}} −\mathrm{25}{x}−\mathrm{5}+\mathrm{30}{x}+\mathrm{16} \\ $$$$=\mathrm{2}{x}^{\mathrm{3}} +\mathrm{5}{x}^{\mathrm{2}} +\mathrm{7}{x}+\mathrm{11}…………..{B} \\ $$$$\boldsymbol{{Comparing}}\:\boldsymbol{{coefficients}}\:{of}\:{A}\:\&{B} \\ $$$$\:\:\:{m}=\mathrm{5}\:\&\:{n}=\mathrm{7} \\ $$
Answered by Rasheed.Sindhi last updated on 09/Sep/21
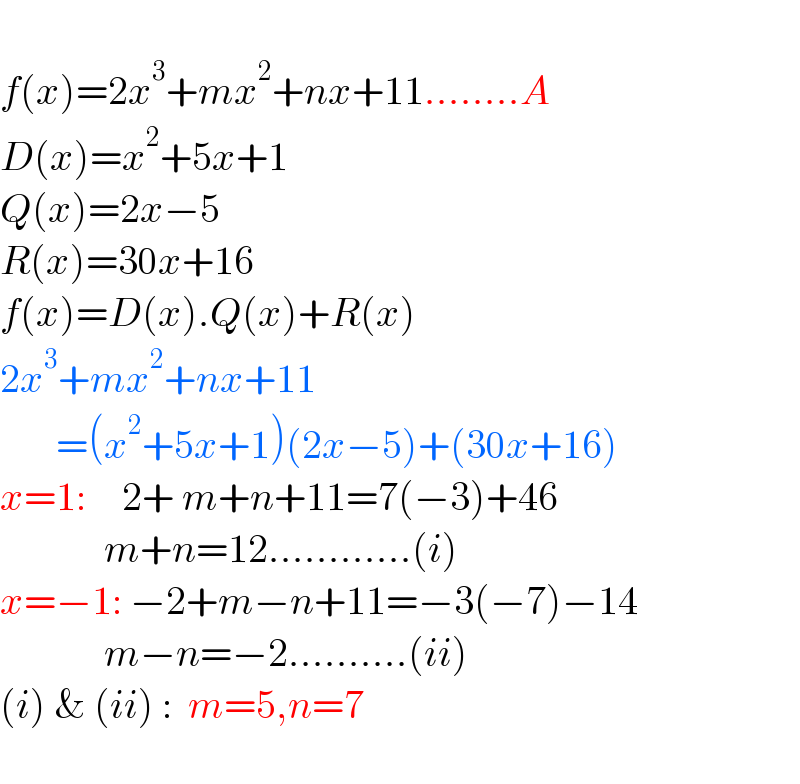
f(x)=2x^3 +mx^2 +nx+11........A D(x)=x^2 +5x+1 Q(x)=2x−5 R(x)=30x+16 f(x)=D(x).Q(x)+R(x) 2x^3 +mx^2 +nx+11 =(x^2 +5x+1)(2x−5)+(30x+16) x=1: 2+ m+n+11=7(−3)+46 m+n=12............(i) x=−1: −2+m−n+11=−3(−7)−14 m−n=−2..........(ii) (i) & (ii) : m=5,n=7
$$ \\ $$$${f}\left({x}\right)=\mathrm{2}{x}^{\mathrm{3}} +{mx}^{\mathrm{2}} +{nx}+\mathrm{11}……..{A} \\ $$$${D}\left({x}\right)={x}^{\mathrm{2}} +\mathrm{5}{x}+\mathrm{1} \\ $$$${Q}\left({x}\right)=\mathrm{2}{x}−\mathrm{5} \\ $$$${R}\left({x}\right)=\mathrm{30}{x}+\mathrm{16} \\ $$$${f}\left({x}\right)={D}\left({x}\right).{Q}\left({x}\right)+{R}\left({x}\right) \\ $$$$\mathrm{2}{x}^{\mathrm{3}} +{mx}^{\mathrm{2}} +{nx}+\mathrm{11} \\ $$$$\:\:\:\:\:\:\:=\left({x}^{\mathrm{2}} +\mathrm{5}{x}+\mathrm{1}\right)\left(\mathrm{2}{x}−\mathrm{5}\right)+\left(\mathrm{30}{x}+\mathrm{16}\right) \\ $$$${x}=\mathrm{1}:\:\:\:\:\:\:\mathrm{2}+\:{m}+{n}+\mathrm{11}=\mathrm{7}\left(−\mathrm{3}\right)+\mathrm{46} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:{m}+{n}=\mathrm{12}…………\left({i}\right) \\ $$$${x}=−\mathrm{1}:\:−\mathrm{2}+{m}−{n}+\mathrm{11}=−\mathrm{3}\left(−\mathrm{7}\right)−\mathrm{14} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:{m}−{n}=−\mathrm{2}……….\left({ii}\right) \\ $$$$\left({i}\right)\:\&\:\left({ii}\right)\::\:\:{m}=\mathrm{5},{n}=\mathrm{7} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *