Question Number 153696 by SANOGO last updated on 09/Sep/21

Answered by puissant last updated on 09/Sep/21
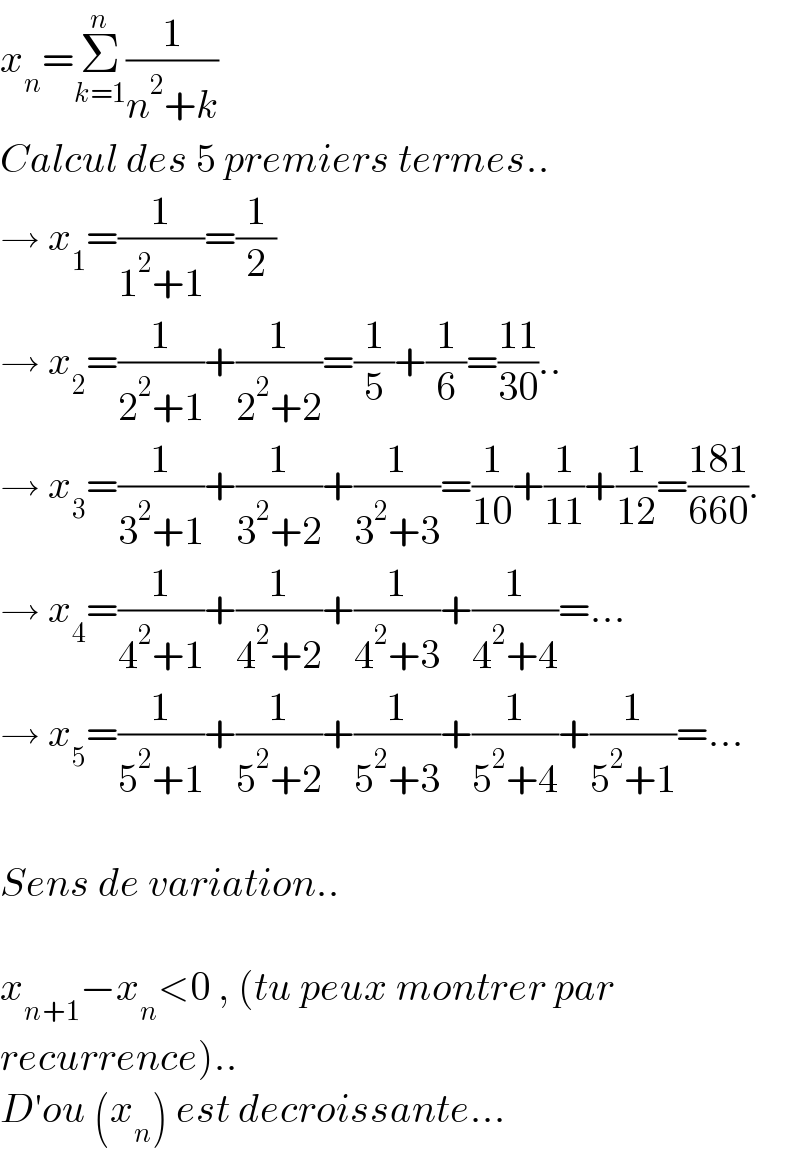
$${x}_{{n}} =\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} +{k}} \\ $$$${Calcul}\:{des}\:\mathrm{5}\:{premiers}\:{termes}.. \\ $$$$\rightarrow\:{x}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{1}^{\mathrm{2}} +\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\rightarrow\:{x}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} +\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} +\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{6}}=\frac{\mathrm{11}}{\mathrm{30}}.. \\ $$$$\rightarrow\:{x}_{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} +\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} +\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} +\mathrm{3}}=\frac{\mathrm{1}}{\mathrm{10}}+\frac{\mathrm{1}}{\mathrm{11}}+\frac{\mathrm{1}}{\mathrm{12}}=\frac{\mathrm{181}}{\mathrm{660}}. \\ $$$$\rightarrow\:{x}_{\mathrm{4}} =\frac{\mathrm{1}}{\mathrm{4}^{\mathrm{2}} +\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{4}^{\mathrm{2}} +\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}^{\mathrm{2}} +\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{4}^{\mathrm{2}} +\mathrm{4}}=… \\ $$$$\rightarrow\:{x}_{\mathrm{5}} =\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{2}} +\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{2}} +\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{2}} +\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{2}} +\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{2}} +\mathrm{1}}=… \\ $$$$ \\ $$$${Sens}\:{de}\:{variation}.. \\ $$$$ \\ $$$${x}_{{n}+\mathrm{1}} −{x}_{{n}} <\mathrm{0}\:,\:\left({tu}\:{peux}\:{montrer}\:{par}\right. \\ $$$$\left.{recurrence}\right).. \\ $$$${D}'{ou}\:\left({x}_{{n}} \right)\:{est}\:{decroissante}… \\ $$
Commented by SANOGO last updated on 09/Sep/21
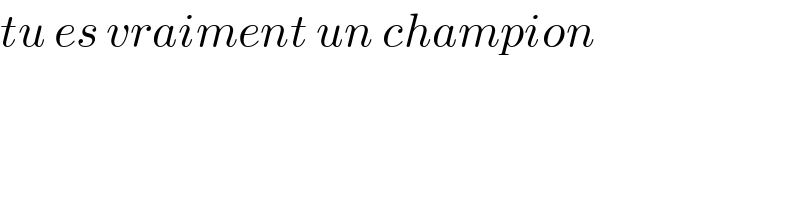
$${tu}\:{es}\:{vraiment}\:{un}\:{champion} \\ $$
