Menu Close

Question-153708

Tinku Tara 0 Comments
Pin




Question Number 153708 by liberty last updated on 09/Sep/21
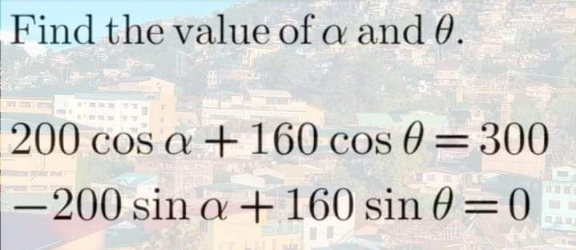
Answered by MJS_new last updated on 09/Sep/21
(1) 200x+160y=300 (2) 200(√(1−x^2 ))=160(√(1−y^2 )) (1) y=((15−10x)/8) (2) 10(√(1−x^2 ))=(√(−100x^2 +300x−161)) ⇒ x=((87)/(100))∧y=((63)/(80)) the rest is easy
$$\left(\mathrm{1}\right)\:\mathrm{200}{x}+\mathrm{160}{y}=\mathrm{300} \\ $$$$\left(\mathrm{2}\right)\:\mathrm{200}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }=\mathrm{160}\sqrt{\mathrm{1}−{y}^{\mathrm{2}} } \\ $$$$ \\ $$$$\left(\mathrm{1}\right)\:{y}=\frac{\mathrm{15}−\mathrm{10}{x}}{\mathrm{8}} \\ $$$$\left(\mathrm{2}\right)\:\mathrm{10}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }=\sqrt{−\mathrm{100}{x}^{\mathrm{2}} +\mathrm{300}{x}−\mathrm{161}} \\ $$$$\Rightarrow\:{x}=\frac{\mathrm{87}}{\mathrm{100}}\wedge{y}=\frac{\mathrm{63}}{\mathrm{80}} \\ $$$$\mathrm{the}\:\mathrm{rest}\:\mathrm{is}\:\mathrm{easy} \\ $$
Commented by pete last updated on 09/Sep/21
wonderful
$$\mathrm{wonderful} \\ $$
Answered by EDWIN88 last updated on 09/Sep/21
⇒sin θ=((200 sin α)/(160))=(5/4)sin α ⇒160cos θ=160(√(1−sin^2 θ)) ⇒160cos θ=160(√(1−((25)/(16))sin^2 α)) =40(√(16−25sin^2 α)) ⇒200cos α+40(√(16−25sin^2 α))=300 ⇒15−10cos α=2(√(16−25sin^2 α)) ⇒225−300cos α+100cos^2 α=64−100sin^2 α ⇒300cos α=325−64 ⇒cos α=((261)/(300)) =((87)/(100)) ; sin α=((√(2431))/(100)) ⇒sin θ=(5/4)×((√(2431))/(100))=((√(2431))/(80)) ; cos θ=((63)/(80))
$$\Rightarrow\mathrm{sin}\:\theta=\frac{\mathrm{200}\:\mathrm{sin}\:\alpha}{\mathrm{160}}=\frac{\mathrm{5}}{\mathrm{4}}\mathrm{sin}\:\alpha \\ $$$$\Rightarrow\mathrm{160cos}\:\theta=\mathrm{160}\sqrt{\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} \theta} \\ $$$$\Rightarrow\mathrm{160cos}\:\theta=\mathrm{160}\sqrt{\mathrm{1}−\frac{\mathrm{25}}{\mathrm{16}}\mathrm{sin}\:^{\mathrm{2}} \alpha} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{40}\sqrt{\mathrm{16}−\mathrm{25sin}\:^{\mathrm{2}} \alpha} \\ $$$$\Rightarrow\mathrm{200cos}\:\alpha+\mathrm{40}\sqrt{\mathrm{16}−\mathrm{25sin}\:^{\mathrm{2}} \alpha}=\mathrm{300} \\ $$$$\Rightarrow\mathrm{15}−\mathrm{10cos}\:\alpha=\mathrm{2}\sqrt{\mathrm{16}−\mathrm{25sin}\:^{\mathrm{2}} \alpha} \\ $$$$\Rightarrow\mathrm{225}−\mathrm{300cos}\:\alpha+\mathrm{100cos}\:^{\mathrm{2}} \alpha=\mathrm{64}−\mathrm{100sin}\:^{\mathrm{2}} \alpha \\ $$$$\Rightarrow\mathrm{300cos}\:\alpha=\mathrm{325}−\mathrm{64} \\ $$$$\Rightarrow\mathrm{cos}\:\alpha=\frac{\mathrm{261}}{\mathrm{300}}\:=\frac{\mathrm{87}}{\mathrm{100}}\:;\:\mathrm{sin}\:\alpha=\frac{\sqrt{\mathrm{2431}}}{\mathrm{100}} \\ $$$$\Rightarrow\mathrm{sin}\:\theta=\frac{\mathrm{5}}{\mathrm{4}}×\frac{\sqrt{\mathrm{2431}}}{\mathrm{100}}=\frac{\sqrt{\mathrm{2431}}}{\mathrm{80}}\:;\:\mathrm{cos}\:\theta=\frac{\mathrm{63}}{\mathrm{80}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *