Question Number 153716 by Rankut last updated on 09/Sep/21

Commented by Rankut last updated on 09/Sep/21

$${help}\:\:{please} \\ $$
Answered by mr W last updated on 09/Sep/21
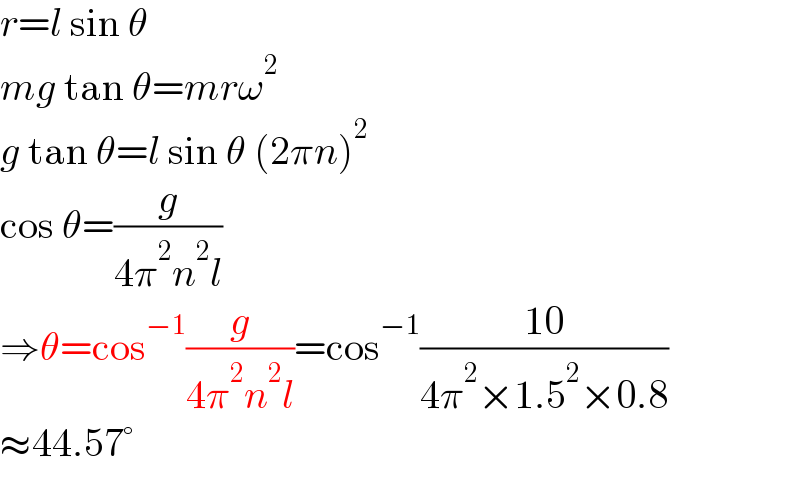
$${r}={l}\:\mathrm{sin}\:\theta \\ $$$${mg}\:\mathrm{tan}\:\theta={mr}\omega^{\mathrm{2}} \\ $$$${g}\:\mathrm{tan}\:\theta={l}\:\mathrm{sin}\:\theta\:\left(\mathrm{2}\pi{n}\right)^{\mathrm{2}} \\ $$$$\mathrm{cos}\:\theta=\frac{{g}}{\mathrm{4}\pi^{\mathrm{2}} {n}^{\mathrm{2}} {l}} \\ $$$$\Rightarrow\theta=\mathrm{cos}^{−\mathrm{1}} \frac{{g}}{\mathrm{4}\pi^{\mathrm{2}} {n}^{\mathrm{2}} {l}}=\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{10}}{\mathrm{4}\pi^{\mathrm{2}} ×\mathrm{1}.\mathrm{5}^{\mathrm{2}} ×\mathrm{0}.\mathrm{8}} \\ $$$$\approx\mathrm{44}.\mathrm{57}° \\ $$
Commented by Rankut last updated on 09/Sep/21

$${thank}\:\:{you}\:\:{sir} \\ $$
