Question Number 153742 by Babatunde last updated on 09/Sep/21
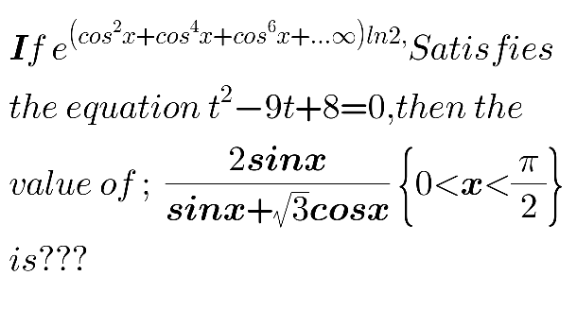
Answered by liberty last updated on 10/Sep/21

$${t}={e}^{\mathrm{ln}\:\mathrm{2}^{\left(\mathrm{cos}\:^{\mathrm{2}} {x}+\mathrm{cos}\:^{\mathrm{4}} {x}+\mathrm{cos}\:^{\mathrm{6}} {x}+…\right)} } \:=\:\mathrm{2}^{\frac{\mathrm{cos}\:^{\mathrm{2}} {x}}{\mathrm{1}−\mathrm{cos}\:^{\mathrm{2}} {x}}} \\ $$$${t}=\mathrm{2}^{\mathrm{cot}\:^{\mathrm{2}} {x}} \\ $$$${the}\:{quadratic}\:{equation} \\ $$$$\Rightarrow\left({t}−\mathrm{1}\right)\left({t}−\mathrm{8}\right)=\mathrm{0}\Rightarrow\begin{cases}{{t}=\mathrm{1}}\\{{t}=\mathrm{8}}\end{cases} \\ $$$$\Rightarrow\mathrm{2}^{\mathrm{cot}\:^{\mathrm{2}} {x}} \:=\:\mathrm{2}^{\mathrm{3}} \:;\:\mathrm{cot}\:^{\mathrm{2}} {x}=\mathrm{3} \\ $$$$\Rightarrow\mathrm{cot}\:{x}=\sqrt{\mathrm{3}}\:;\left(\mathrm{0}<{x}<\frac{\pi}{\mathrm{2}}\right) \\ $$$$\Rightarrow\mathrm{tan}\:{x}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:\Rightarrow{x}=\frac{\pi}{\mathrm{6}} \\ $$$${then}\:\frac{\mathrm{2sin}\:{x}}{\mathrm{sin}\:{x}+\sqrt{\mathrm{3}}\:\mathrm{cos}\:{x}}\:=\:\frac{\mathrm{1}}{\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}}\:=\mathrm{1} \\ $$
