Menu Close

Question-153757

Tinku Tara 0 Comments
Pin




Question Number 153757 by liberty last updated on 10/Sep/21
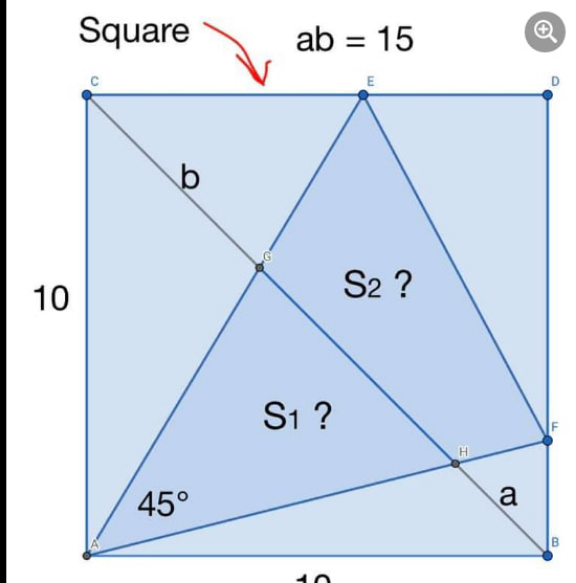
Commented by mr W last updated on 11/Sep/21
S_1 =S_2 =((85)/4)
$${S}_{\mathrm{1}} ={S}_{\mathrm{2}} =\frac{\mathrm{85}}{\mathrm{4}} \\ $$
Answered by mr W last updated on 11/Sep/21
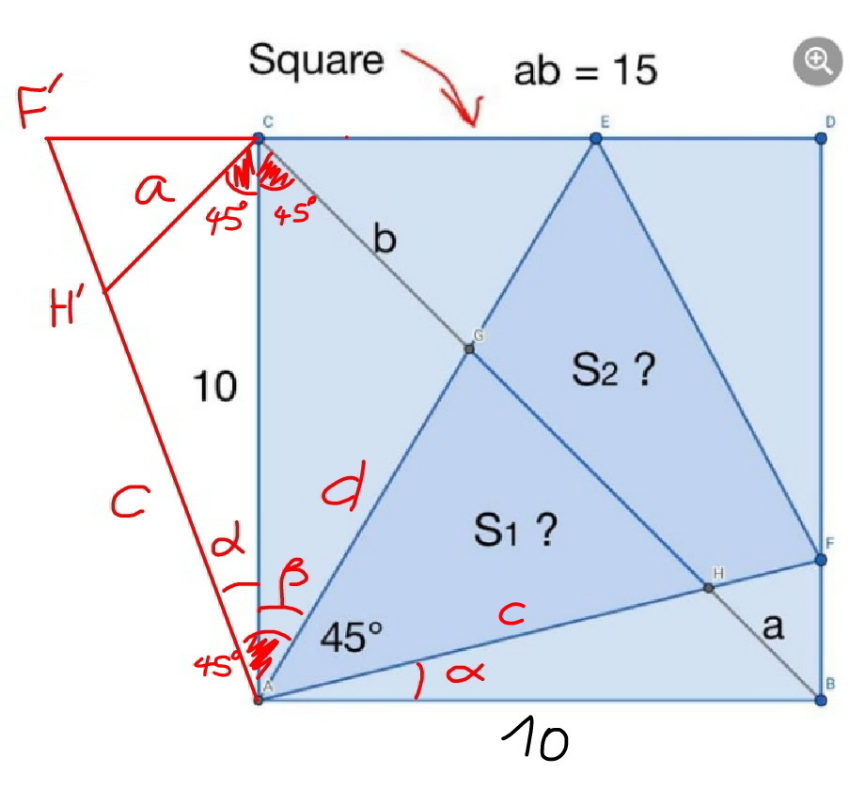
Commented by mr W last updated on 11/Sep/21
((sin (45+α))/(sin α))=((10)/a) (1/( (√2)))((1/(tan α))+1)=((10)/a) ⇒(1/(tan α))=((10(√2))/a)−1 ((sin (45+β))/(sin β))=((10)/b) (1/( (√2)))((1/(tan β))+1)=((10)/b) ⇒(1/(tan β))=((10(√2))/b)−1 α+β=45° tan (α+β)=1 ((tan α+tan β)/(1−tan α tan β))=1 tan α+tan β=1−tan α tan β (1/(tan α))+(1/(tan β))=(1/(tan α))×(1/(tan β))−1 ((10(√2))/a)−1+((10(√2))/b)−1=(((10(√2))/a)−1)×(((10(√2))/b)−1)−1 ((10(√2))/a)+((10(√2))/b)−1=((100)/(ab)) ((10(√2)(a+b))/(ab))−1=((100)/(ab)) ab=15 ⇒a+b=((23(√2))/4) a,b are roots of x^2 −((23(√2))/4)x+15=0 ⇒a,b=(((23±7)(√2))/8)= { ((2(√2))),(((15(√2))/4)) :} (1/(tan α))=((10(√2))/(2(√2)))−1=4 ⇒tan α=(1/4) (1/(tan β))=((10(√2))/((15(√2))/4))=(5/( 3)) ⇒tan β=(3/5) (c/a)=((sin 45)/(sin α)) ⇒c=((2(√2))/( (√2)×(1/( (√(17))))))=2(√(17)) (d/b)=((sin 45)/(sin β)) ⇒d=((15(√2))/( 4(√2)×(3/( (√(34))))))=((5(√(34)))/4) S_1 =((cd sin 45°)/2) =(1/(2(√2)))×2(√(17))×((5(√(34)))/4)=((85)/4) AE=((10)/(cos β))=((10)/(5/( (√(34)))))=2(√(34)) AF=((10)/(cos α))=((10)/( (4/( (√(17))))))=((5(√(17)))/2) S_1 +S_2 =((AE×AF×sin 45°)/2) =(1/(2(√2)))×2(√(34))×((5(√(17)))/( 2))=((85)/2) ⇒S_2 =((85)/2)−((85)/4)=((85)/4)=S_1
$$\frac{\mathrm{sin}\:\left(\mathrm{45}+\alpha\right)}{\mathrm{sin}\:\alpha}=\frac{\mathrm{10}}{{a}} \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left(\frac{\mathrm{1}}{\mathrm{tan}\:\alpha}+\mathrm{1}\right)=\frac{\mathrm{10}}{{a}} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{tan}\:\alpha}=\frac{\mathrm{10}\sqrt{\mathrm{2}}}{{a}}−\mathrm{1} \\ $$$$\frac{\mathrm{sin}\:\left(\mathrm{45}+\beta\right)}{\mathrm{sin}\:\beta}=\frac{\mathrm{10}}{{b}} \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left(\frac{\mathrm{1}}{\mathrm{tan}\:\beta}+\mathrm{1}\right)=\frac{\mathrm{10}}{{b}} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{tan}\:\beta}=\frac{\mathrm{10}\sqrt{\mathrm{2}}}{{b}}−\mathrm{1} \\ $$$$\alpha+\beta=\mathrm{45}° \\ $$$$\mathrm{tan}\:\left(\alpha+\beta\right)=\mathrm{1} \\ $$$$\frac{\mathrm{tan}\:\alpha+\mathrm{tan}\:\beta}{\mathrm{1}−\mathrm{tan}\:\alpha\:\mathrm{tan}\:\beta}=\mathrm{1} \\ $$$$\mathrm{tan}\:\alpha+\mathrm{tan}\:\beta=\mathrm{1}−\mathrm{tan}\:\alpha\:\mathrm{tan}\:\beta \\ $$$$\frac{\mathrm{1}}{\mathrm{tan}\:\alpha}+\frac{\mathrm{1}}{\mathrm{tan}\:\beta}=\frac{\mathrm{1}}{\mathrm{tan}\:\alpha}×\frac{\mathrm{1}}{\mathrm{tan}\:\beta}−\mathrm{1} \\ $$$$\frac{\mathrm{10}\sqrt{\mathrm{2}}}{{a}}−\mathrm{1}+\frac{\mathrm{10}\sqrt{\mathrm{2}}}{{b}}−\mathrm{1}=\left(\frac{\mathrm{10}\sqrt{\mathrm{2}}}{{a}}−\mathrm{1}\right)×\left(\frac{\mathrm{10}\sqrt{\mathrm{2}}}{{b}}−\mathrm{1}\right)−\mathrm{1} \\ $$$$\frac{\mathrm{10}\sqrt{\mathrm{2}}}{{a}}+\frac{\mathrm{10}\sqrt{\mathrm{2}}}{{b}}−\mathrm{1}=\frac{\mathrm{100}}{{ab}} \\ $$$$\frac{\mathrm{10}\sqrt{\mathrm{2}}\left({a}+{b}\right)}{{ab}}−\mathrm{1}=\frac{\mathrm{100}}{{ab}} \\ $$$${ab}=\mathrm{15} \\ $$$$\Rightarrow{a}+{b}=\frac{\mathrm{23}\sqrt{\mathrm{2}}}{\mathrm{4}} \\ $$$${a},{b}\:{are}\:{roots}\:{of} \\ $$$${x}^{\mathrm{2}} −\frac{\mathrm{23}\sqrt{\mathrm{2}}}{\mathrm{4}}{x}+\mathrm{15}=\mathrm{0} \\ $$$$\Rightarrow{a},{b}=\frac{\left(\mathrm{23}\pm\mathrm{7}\right)\sqrt{\mathrm{2}}}{\mathrm{8}}=\begin{cases}{\mathrm{2}\sqrt{\mathrm{2}}}\\{\frac{\mathrm{15}\sqrt{\mathrm{2}}}{\mathrm{4}}}\end{cases} \\ $$$$\frac{\mathrm{1}}{\mathrm{tan}\:\alpha}=\frac{\mathrm{10}\sqrt{\mathrm{2}}}{\mathrm{2}\sqrt{\mathrm{2}}}−\mathrm{1}=\mathrm{4}\:\Rightarrow\mathrm{tan}\:\alpha=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\frac{\mathrm{1}}{\mathrm{tan}\:\beta}=\frac{\mathrm{10}\sqrt{\mathrm{2}}}{\frac{\mathrm{15}\sqrt{\mathrm{2}}}{\mathrm{4}}}=\frac{\mathrm{5}}{\:\mathrm{3}}\:\Rightarrow\mathrm{tan}\:\beta=\frac{\mathrm{3}}{\mathrm{5}} \\ $$$$\frac{{c}}{{a}}=\frac{\mathrm{sin}\:\mathrm{45}}{\mathrm{sin}\:\alpha}\:\Rightarrow{c}=\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{2}}×\frac{\mathrm{1}}{\:\sqrt{\mathrm{17}}}}=\mathrm{2}\sqrt{\mathrm{17}} \\ $$$$\frac{{d}}{{b}}=\frac{\mathrm{sin}\:\mathrm{45}}{\mathrm{sin}\:\beta}\:\Rightarrow{d}=\frac{\mathrm{15}\sqrt{\mathrm{2}}}{\:\mathrm{4}\sqrt{\mathrm{2}}×\frac{\mathrm{3}}{\:\sqrt{\mathrm{34}}}}=\frac{\mathrm{5}\sqrt{\mathrm{34}}}{\mathrm{4}} \\ $$$${S}_{\mathrm{1}} =\frac{{cd}\:\mathrm{sin}\:\mathrm{45}°}{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}×\mathrm{2}\sqrt{\mathrm{17}}×\frac{\mathrm{5}\sqrt{\mathrm{34}}}{\mathrm{4}}=\frac{\mathrm{85}}{\mathrm{4}} \\ $$$${AE}=\frac{\mathrm{10}}{\mathrm{cos}\:\beta}=\frac{\mathrm{10}}{\frac{\mathrm{5}}{\:\sqrt{\mathrm{34}}}}=\mathrm{2}\sqrt{\mathrm{34}} \\ $$$${AF}=\frac{\mathrm{10}}{\mathrm{cos}\:\alpha}=\frac{\mathrm{10}}{\:\frac{\mathrm{4}}{\:\sqrt{\mathrm{17}}}}=\frac{\mathrm{5}\sqrt{\mathrm{17}}}{\mathrm{2}} \\ $$$${S}_{\mathrm{1}} +{S}_{\mathrm{2}} =\frac{{AE}×{AF}×\mathrm{sin}\:\mathrm{45}°}{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}×\mathrm{2}\sqrt{\mathrm{34}}×\frac{\mathrm{5}\sqrt{\mathrm{17}}}{\:\mathrm{2}}=\frac{\mathrm{85}}{\mathrm{2}} \\ $$$$\Rightarrow{S}_{\mathrm{2}} =\frac{\mathrm{85}}{\mathrm{2}}−\frac{\mathrm{85}}{\mathrm{4}}=\frac{\mathrm{85}}{\mathrm{4}}={S}_{\mathrm{1}} \\ $$
Commented by Ari last updated on 11/Sep/21
Mr.W. always, the ratio S2/S1 eshte 1 if dhe angle 0f triangle is 45 grade?
Commented by mr W last updated on 11/Sep/21
yes, S_1 =S_2 is always true.
$${yes},\:{S}_{\mathrm{1}} ={S}_{\mathrm{2}} \:{is}\:{always}\:{true}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *