Menu Close

Question-153858

Tinku Tara 0 Comments
Pin




Question Number 153858 by liberty last updated on 11/Sep/21
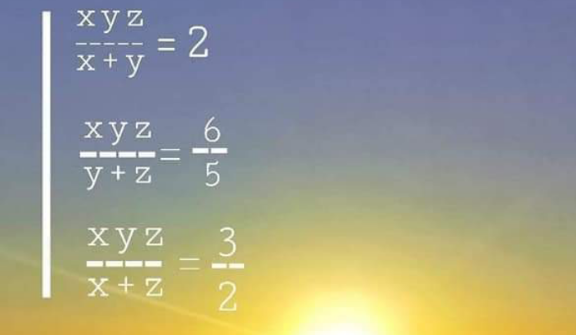
Commented by liberty last updated on 11/Sep/21
{ ((x=?)),((y=?)),((z=?)) :}
$$\:\begin{cases}{{x}=?}\\{{y}=?}\\{{z}=?}\end{cases} \\ $$
Answered by EDWIN88 last updated on 11/Sep/21
{ ((((x+y)/(xyz))=(1/2)⇒(1/(yz))+(1/(xz))=(1/2))),(( ((y+z)/(xyz))=(5/6)⇒(1/(xz))+(1/(xy))=(5/6))),((((x+z)/(xyz))=(2/3)⇒(1/(yz))+(1/(xy))=(2/3))) :} ⇒2((1/(xy))+(1/(xz))+(1/(yz)))=2 ⇒(1/(xy))+(1/(xz))+(1/(yz))=1 → { (((1/(xy))=(1/2))),(((1/(xz))=(1/3))),(((1/(yz))=(1/6))) :} ⇒(1/((xyz)^2 )) = (1/(36)) →(1/(xyz)) =±(1/6)→ { ((z=±3)),((x=±1)),((y=±2)) :}
$$\:\begin{cases}{\frac{{x}+{y}}{{xyz}}=\frac{\mathrm{1}}{\mathrm{2}}\Rightarrow\frac{\mathrm{1}}{{yz}}+\frac{\mathrm{1}}{{xz}}=\frac{\mathrm{1}}{\mathrm{2}}}\\{\:\:\frac{{y}+{z}}{{xyz}}=\frac{\mathrm{5}}{\mathrm{6}}\Rightarrow\frac{\mathrm{1}}{{xz}}+\frac{\mathrm{1}}{{xy}}=\frac{\mathrm{5}}{\mathrm{6}}}\\{\frac{{x}+{z}}{{xyz}}=\frac{\mathrm{2}}{\mathrm{3}}\Rightarrow\frac{\mathrm{1}}{{yz}}+\frac{\mathrm{1}}{{xy}}=\frac{\mathrm{2}}{\mathrm{3}}}\end{cases} \\ $$$$\Rightarrow\mathrm{2}\left(\frac{\mathrm{1}}{{xy}}+\frac{\mathrm{1}}{{xz}}+\frac{\mathrm{1}}{{yz}}\right)=\mathrm{2} \\ $$$$\Rightarrow\frac{\mathrm{1}}{{xy}}+\frac{\mathrm{1}}{{xz}}+\frac{\mathrm{1}}{{yz}}=\mathrm{1}\:\rightarrow\begin{cases}{\frac{\mathrm{1}}{{xy}}=\frac{\mathrm{1}}{\mathrm{2}}}\\{\frac{\mathrm{1}}{{xz}}=\frac{\mathrm{1}}{\mathrm{3}}}\\{\frac{\mathrm{1}}{{yz}}=\frac{\mathrm{1}}{\mathrm{6}}}\end{cases} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\left({xyz}\right)^{\mathrm{2}} }\:=\:\frac{\mathrm{1}}{\mathrm{36}} \\ $$$$\rightarrow\frac{\mathrm{1}}{{xyz}}\:=\pm\frac{\mathrm{1}}{\mathrm{6}}\rightarrow\begin{cases}{{z}=\pm\mathrm{3}}\\{{x}=\pm\mathrm{1}}\\{{y}=\pm\mathrm{2}}\end{cases} \\ $$
Commented by Tawa11 last updated on 12/Sep/21
Weldone sir
$$\mathrm{Weldone}\:\mathrm{sir} \\ $$
Answered by Rasheed.Sindhi last updated on 11/Sep/21
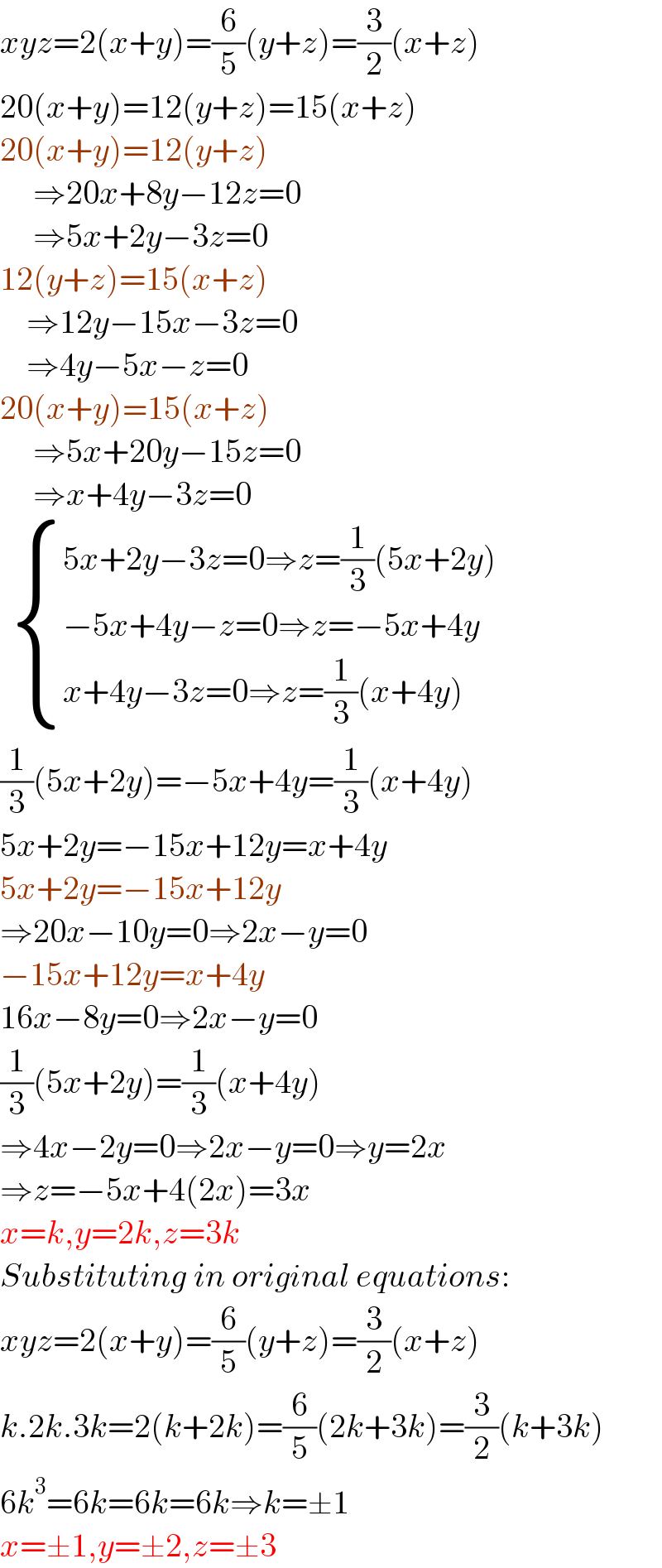
xyz=2(x+y)=(6/5)(y+z)=(3/2)(x+z) 20(x+y)=12(y+z)=15(x+z) 20(x+y)=12(y+z) ⇒20x+8y−12z=0 ⇒5x+2y−3z=0 12(y+z)=15(x+z) ⇒12y−15x−3z=0 ⇒4y−5x−z=0 20(x+y)=15(x+z) ⇒5x+20y−15z=0 ⇒x+4y−3z=0 { ((5x+2y−3z=0⇒z=(1/3)(5x+2y))),((−5x+4y−z=0⇒z=−5x+4y )),((x+4y−3z=0⇒z=(1/3)(x+4y))) :} (1/3)(5x+2y)=−5x+4y=(1/3)(x+4y) 5x+2y=−15x+12y=x+4y 5x+2y=−15x+12y ⇒20x−10y=0⇒2x−y=0 −15x+12y=x+4y 16x−8y=0⇒2x−y=0 (1/3)(5x+2y)=(1/3)(x+4y) ⇒4x−2y=0⇒2x−y=0⇒y=2x ⇒z=−5x+4(2x)=3x x=k,y=2k,z=3k Substituting in original equations: xyz=2(x+y)=(6/5)(y+z)=(3/2)(x+z) k.2k.3k=2(k+2k)=(6/5)(2k+3k)=(3/2)(k+3k) 6k^3 =6k=6k=6k⇒k=±1 x=±1,y=±2,z=±3
$${xyz}=\mathrm{2}\left({x}+{y}\right)=\frac{\mathrm{6}}{\mathrm{5}}\left({y}+{z}\right)=\frac{\mathrm{3}}{\mathrm{2}}\left({x}+{z}\right) \\ $$$$\mathrm{20}\left({x}+{y}\right)=\mathrm{12}\left({y}+{z}\right)=\mathrm{15}\left({x}+{z}\right) \\ $$$$\mathrm{20}\left({x}+{y}\right)=\mathrm{12}\left({y}+{z}\right) \\ $$$$\:\:\:\:\:\Rightarrow\mathrm{20}{x}+\mathrm{8}{y}−\mathrm{12}{z}=\mathrm{0} \\ $$$$\:\:\:\:\:\Rightarrow\mathrm{5}{x}+\mathrm{2}{y}−\mathrm{3}{z}=\mathrm{0} \\ $$$$\mathrm{12}\left({y}+{z}\right)=\mathrm{15}\left({x}+{z}\right) \\ $$$$\:\:\:\:\Rightarrow\mathrm{12}{y}−\mathrm{15}{x}−\mathrm{3}{z}=\mathrm{0} \\ $$$$\:\:\:\:\Rightarrow\mathrm{4}{y}−\mathrm{5}{x}−{z}=\mathrm{0} \\ $$$$\mathrm{20}\left({x}+{y}\right)=\mathrm{15}\left({x}+{z}\right) \\ $$$$\:\:\:\:\:\Rightarrow\mathrm{5}{x}+\mathrm{20}{y}−\mathrm{15}{z}=\mathrm{0} \\ $$$$\:\:\:\:\:\Rightarrow{x}+\mathrm{4}{y}−\mathrm{3}{z}=\mathrm{0} \\ $$$$\:\:\begin{cases}{\mathrm{5}{x}+\mathrm{2}{y}−\mathrm{3}{z}=\mathrm{0}\Rightarrow{z}=\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{5}{x}+\mathrm{2}{y}\right)}\\{−\mathrm{5}{x}+\mathrm{4}{y}−{z}=\mathrm{0}\Rightarrow{z}=−\mathrm{5}{x}+\mathrm{4}{y}\:\:\:}\\{{x}+\mathrm{4}{y}−\mathrm{3}{z}=\mathrm{0}\Rightarrow{z}=\frac{\mathrm{1}}{\mathrm{3}}\left({x}+\mathrm{4}{y}\right)}\end{cases} \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{5}{x}+\mathrm{2}{y}\right)=−\mathrm{5}{x}+\mathrm{4}{y}=\frac{\mathrm{1}}{\mathrm{3}}\left({x}+\mathrm{4}{y}\right) \\ $$$$\mathrm{5}{x}+\mathrm{2}{y}=−\mathrm{15}{x}+\mathrm{12}{y}={x}+\mathrm{4}{y} \\ $$$$\mathrm{5}{x}+\mathrm{2}{y}=−\mathrm{15}{x}+\mathrm{12}{y} \\ $$$$\Rightarrow\mathrm{20}{x}−\mathrm{10}{y}=\mathrm{0}\Rightarrow\mathrm{2}{x}−{y}=\mathrm{0} \\ $$$$−\mathrm{15}{x}+\mathrm{12}{y}={x}+\mathrm{4}{y} \\ $$$$\mathrm{16}{x}−\mathrm{8}{y}=\mathrm{0}\Rightarrow\mathrm{2}{x}−{y}=\mathrm{0} \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{5}{x}+\mathrm{2}{y}\right)=\frac{\mathrm{1}}{\mathrm{3}}\left({x}+\mathrm{4}{y}\right) \\ $$$$\Rightarrow\mathrm{4}{x}−\mathrm{2}{y}=\mathrm{0}\Rightarrow\mathrm{2}{x}−{y}=\mathrm{0}\Rightarrow{y}=\mathrm{2}{x} \\ $$$$\Rightarrow{z}=−\mathrm{5}{x}+\mathrm{4}\left(\mathrm{2}{x}\right)=\mathrm{3}{x} \\ $$$${x}={k},{y}=\mathrm{2}{k},{z}=\mathrm{3}{k} \\ $$$${Substituting}\:{in}\:{original}\:{equations}: \\ $$$${xyz}=\mathrm{2}\left({x}+{y}\right)=\frac{\mathrm{6}}{\mathrm{5}}\left({y}+{z}\right)=\frac{\mathrm{3}}{\mathrm{2}}\left({x}+{z}\right) \\ $$$${k}.\mathrm{2}{k}.\mathrm{3}{k}=\mathrm{2}\left({k}+\mathrm{2}{k}\right)=\frac{\mathrm{6}}{\mathrm{5}}\left(\mathrm{2}{k}+\mathrm{3}{k}\right)=\frac{\mathrm{3}}{\mathrm{2}}\left({k}+\mathrm{3}{k}\right) \\ $$$$\mathrm{6}{k}^{\mathrm{3}} =\mathrm{6}{k}=\mathrm{6}{k}=\mathrm{6}{k}\Rightarrow{k}=\pm\mathrm{1} \\ $$$${x}=\pm\mathrm{1},{y}=\pm\mathrm{2},{z}=\pm\mathrm{3} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *