Question Number 153860 by SANOGO last updated on 11/Sep/21
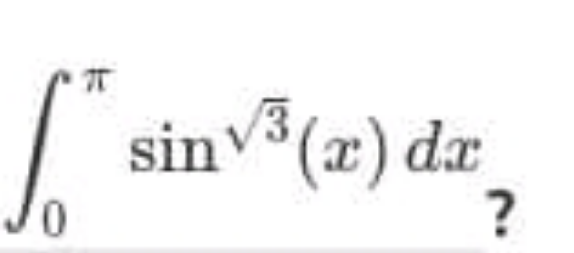
Answered by puissant last updated on 11/Sep/21

$${Q}=\int_{\mathrm{0}} ^{\pi} {sin}^{\sqrt{\mathrm{3}}} {x}\:{dx} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {sin}^{\sqrt{\mathrm{3}}} {x}\:{dx} \\ $$$$\rightarrow\:{I}=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {sin}^{\sqrt{\mathrm{3}}} {x}\:{dx} \\ $$$${posons}\:\:{f}\left(\alpha\right)=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {sin}^{\alpha−\mathrm{1}} {x}\:{dx} \\ $$$$\Rightarrow\:{f}\left(\alpha\right)=\frac{\mathrm{1}}{\mathrm{2}}\beta\left(\frac{\alpha}{\mathrm{2}};\frac{\mathrm{1}}{\mathrm{2}}\right)=\frac{\sqrt{\pi}\:\Gamma\left(\frac{\alpha}{\mathrm{2}}\right)}{\mathrm{2}\Gamma\left(\frac{\alpha+\mathrm{1}}{\mathrm{2}}\right)} \\ $$$${pour}\:\alpha=\sqrt{\mathrm{3}}+\mathrm{1},\:{on}\:{a}: \\ $$$${Q}\:=\:\mathrm{2}×\frac{\sqrt{\pi}\:\Gamma\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\right)}{\mathrm{2}\Gamma\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}+\mathrm{1}\right)}.. \\ $$$$\therefore\because\:\:{Q}=\frac{\sqrt{\pi}\:\Gamma\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\right)}{\Gamma\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}+\mathrm{1}\right)}…. \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:……….\mathscr{L}{e}\:{puissant}………. \\ $$
Commented by SANOGO last updated on 11/Sep/21

$${toujour}\:{le}\:{cerveau}\:{des}\:{cerveau}\:{merci} \\ $$
Commented by SANOGO last updated on 11/Sep/21

$${propre}\:{mon}\:{superieur} \\ $$
