Question-153912

Question Number 153912 by cherokeesay last updated on 12/Sep/21

Answered by mr W last updated on 12/Sep/21

Commented by mr W last updated on 12/Sep/21

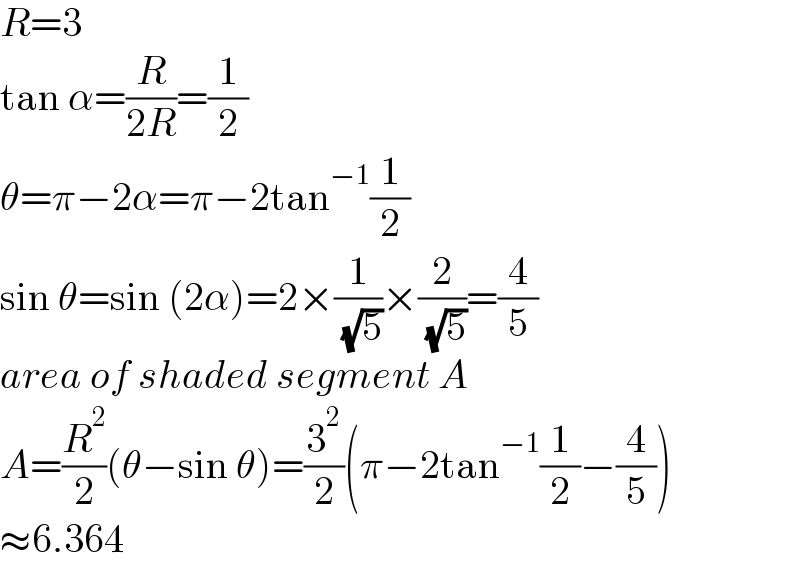
R=3 tan α=(R/(2R))=(1/2) θ=π−2α=π−2tan^(−1) (1/2) sin θ=sin (2α)=2×(1/( (√5)))×(2/( (√5)))=(4/5) area of shaded segment A A=(R^2 /2)(θ−sin θ)=(3^2 /2)(π−2tan^(−1) (1/2)−(4/5)) ≈6.364

$${R}=\mathrm{3} \\ $$$$\mathrm{tan}\:\alpha=\frac{{R}}{\mathrm{2}{R}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\theta=\pi−\mathrm{2}\alpha=\pi−\mathrm{2tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{sin}\:\theta=\mathrm{sin}\:\left(\mathrm{2}\alpha\right)=\mathrm{2}×\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}×\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}=\frac{\mathrm{4}}{\mathrm{5}} \\ $$$${area}\:{of}\:{shaded}\:{segment}\:{A} \\ $$$${A}=\frac{{R}^{\mathrm{2}} }{\mathrm{2}}\left(\theta−\mathrm{sin}\:\theta\right)=\frac{\mathrm{3}^{\mathrm{2}} }{\mathrm{2}}\left(\pi−\mathrm{2tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{4}}{\mathrm{5}}\right) \\ $$$$\approx\mathrm{6}.\mathrm{364} \\ $$

Commented by Tawa11 last updated on 12/Sep/21

$$\mathrm{Weldone}\:\mathrm{sir} \\ $$

Commented by cherokeesay last updated on 12/Sep/21

$${it}'{s}\:{very}\:{beautiful}\:! \\ $$$${thank}\:{you}\:{mr}\:{W}\:! \\ $$

Commented by talminator2856791 last updated on 12/Sep/21

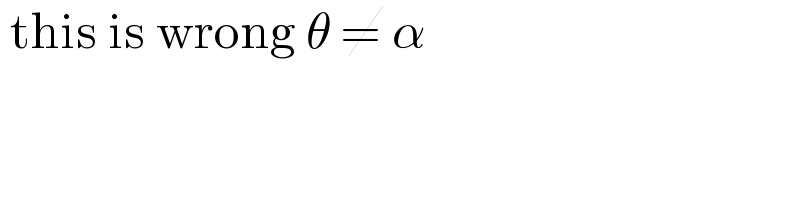
$$\:\mathrm{this}\:\mathrm{is}\:\mathrm{wrong}\:\theta\:\neq\:\alpha \\ $$

Commented by mr W last updated on 12/Sep/21

$${who}\:{said}\:\theta=\alpha?\:{didn}'{t}\:{you}\:{see} \\ $$$$\theta=\pi−\mathrm{2}\alpha? \\ $$

Answered by talminator2856791 last updated on 12/Sep/21

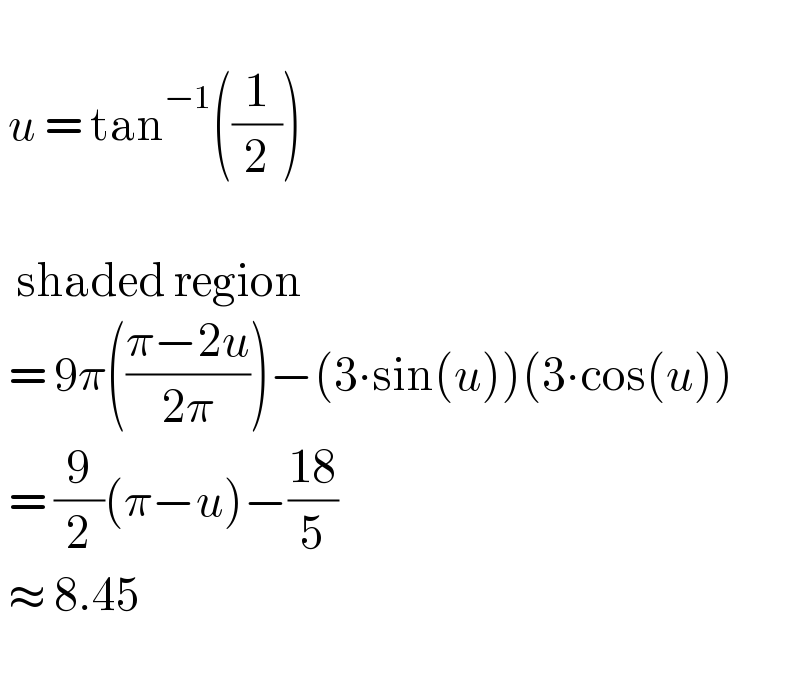
u = tan^(−1) ((1/2)) shaded region = 9π(((π−2u)/(2π)))−(3∙sin(u))(3∙cos(u)) = (9/2)(π−u)−((18)/5) ≈ 8.45

$$\: \\ $$$$\:{u}\:=\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\: \\ $$$$\:\:\mathrm{shaded}\:\mathrm{region} \\ $$$$\:=\:\mathrm{9}\pi\left(\frac{\pi−\mathrm{2}{u}}{\mathrm{2}\pi}\right)−\left(\mathrm{3}\centerdot\mathrm{sin}\left({u}\right)\right)\left(\mathrm{3}\centerdot\mathrm{cos}\left({u}\right)\right)\: \\ $$$$\:=\:\frac{\mathrm{9}}{\mathrm{2}}\left(\pi−{u}\right)−\frac{\mathrm{18}}{\mathrm{5}} \\ $$$$\:\approx\:\mathrm{8}.\mathrm{45} \\ $$$$\: \\ $$

Commented by cherokeesay last updated on 12/Sep/21

numerically : A_(A.S.P) = ((π.9[180°−(2×26,565°)])/(360°)) −3,6= = 9,96 − 3,6 = 6,36 cm^2

$${numerically}\:: \\ $$$$\mathscr{A}_{{A}.{S}.{P}} =\:\frac{\pi.\mathrm{9}\left[\mathrm{180}°−\left(\mathrm{2}×\mathrm{26},\mathrm{565}°\right)\right]}{\mathrm{360}°}\:−\mathrm{3},\mathrm{6}= \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{9},\mathrm{96}\:−\:\mathrm{3},\mathrm{6}\:=\:\mathrm{6},\mathrm{36}\:{cm}^{\mathrm{2}} \\ $$

Commented by cherokeesay last updated on 12/Sep/21

$${thank}\:{you}\:{sir}\:! \\ $$

Commented by mr W last updated on 12/Sep/21

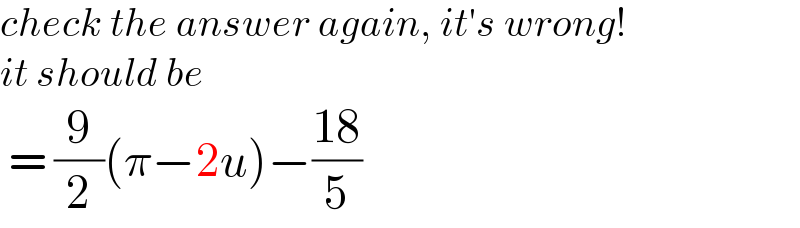
check the answer again, it′s wrong! it should be = (9/2)(π−2u)−((18)/5)

$${check}\:{the}\:{answer}\:{again},\:{it}'{s}\:{wrong}!\: \\ $$$${it}\:{should}\:{be} \\ $$$$\:=\:\frac{\mathrm{9}}{\mathrm{2}}\left(\pi−\mathrm{2}{u}\right)−\frac{\mathrm{18}}{\mathrm{5}} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply