Question Number 153915 by liberty last updated on 12/Sep/21
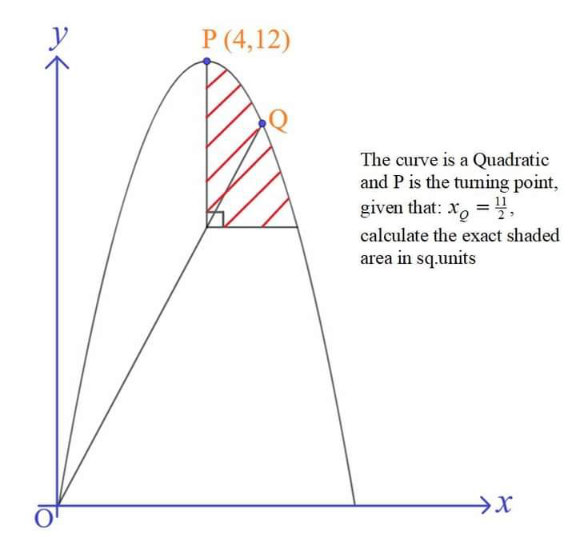
Answered by mr W last updated on 12/Sep/21

Commented by mr W last updated on 12/Sep/21

$${AQ}=\frac{\mathrm{11}}{\mathrm{2}}−\mathrm{4}=\frac{\mathrm{3}}{\mathrm{2}} \\ $$$${DQ}=\left(\frac{\:\frac{\mathrm{3}}{\mathrm{2}}\:}{\mathrm{4}}\right)^{\mathrm{2}} ×\mathrm{12}=\frac{\mathrm{27}}{\mathrm{16}} \\ $$$${AC}=\mathrm{12}−{DQ}=\mathrm{12}−\frac{\mathrm{27}}{\mathrm{16}}=\frac{\mathrm{165}}{\mathrm{16}} \\ $$$$\frac{{BC}}{{AB}}=\frac{{OC}}{{AQ}}=\frac{\mathrm{4}}{\frac{\mathrm{3}}{\mathrm{2}}}=\frac{\mathrm{8}}{\mathrm{3}} \\ $$$$\frac{\frac{\mathrm{165}}{\mathrm{16}}−{AB}}{{AB}}=\frac{\mathrm{8}}{\mathrm{3}} \\ $$$$\frac{\frac{\mathrm{165}}{\mathrm{16}}}{{AB}}=\frac{\mathrm{11}}{\mathrm{3}} \\ $$$${AB}=\frac{\mathrm{165}}{\mathrm{16}}×\frac{\mathrm{3}}{\mathrm{11}}=\frac{\mathrm{45}}{\mathrm{16}} \\ $$$${ER}={DQ}+{AB}=\frac{\mathrm{27}}{\mathrm{16}}+\frac{\mathrm{45}}{\mathrm{16}}=\frac{\mathrm{9}}{\mathrm{2}} \\ $$$${ER}=\left(\frac{{BR}}{\mathrm{4}}\right)^{\mathrm{2}} ×\mathrm{12}=\frac{\mathrm{9}}{\mathrm{2}} \\ $$$$\Rightarrow{BR}=\sqrt{\mathrm{6}} \\ $$$${shaded}\:{area}=\frac{\mathrm{2}}{\mathrm{3}}×{BR}×{ER} \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}×\sqrt{\mathrm{6}}×\frac{\mathrm{9}}{\mathrm{2}}=\mathrm{3}\sqrt{\mathrm{6}} \\ $$
Commented by Tawa11 last updated on 12/Sep/21

$$\mathrm{Weldone}\:\mathrm{sir}. \\ $$
Commented by mr W last updated on 12/Sep/21

$${can}\:{your}\:{comment}\:{be}\:{understood}\:{that} \\ $$$${the}\:{answer}\:{is}\:{correct}? \\ $$
Commented by Tawa11 last updated on 12/Sep/21

$$\mathrm{No}\:\mathrm{sir},\:\mathrm{I}\:\mathrm{am}\:\mathrm{going}\:\mathrm{through}\:\mathrm{your}\:\mathrm{workings}.\:\mathrm{Learning}\:\mathrm{the}\:\mathrm{steps}. \\ $$
Commented by liberty last updated on 12/Sep/21

$${yes}.\:{i}\:{got}\:{the}\:{same}\:{answer} \\ $$
