Menu Close

Question-153958

Tinku Tara 0 Comments
Pin




Question Number 153958 by DELETED last updated on 12/Sep/21
Answered by DELETED last updated on 12/Sep/21
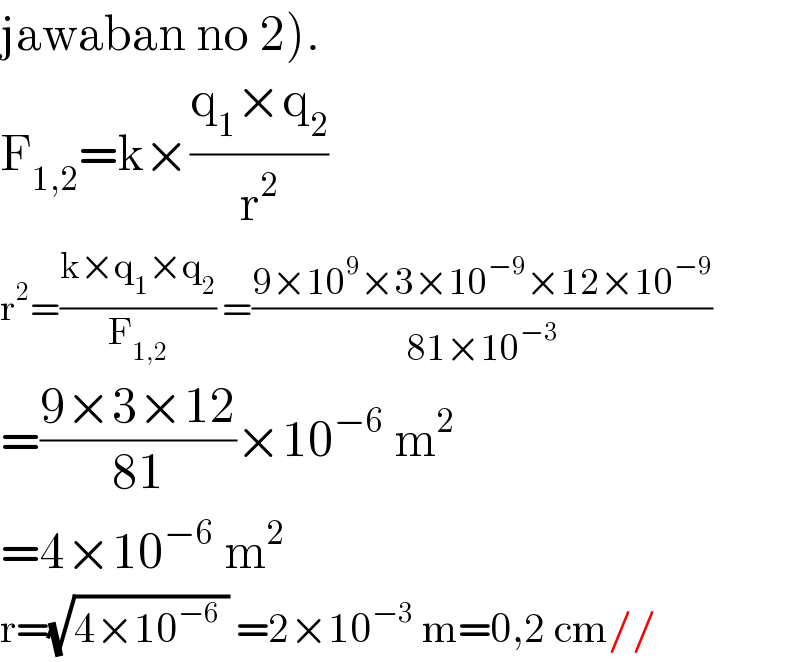
jawaban no 2). F_(1,2) =k×((q_1 ×q_2 )/r^2 ) r^2 =((k×q_1 ×q_2 )/F_(1,2) ) =((9×10^9 ×3×10^(−9) ×12×10^(−9) )/(81×10^(−3) )) =((9×3×12)/(81))×10^(−6) m^2 =4×10^(−6) m^2 r=(√(4×10^(−6) )) =2×10^(−3) m=0,2 cm//
$$\left.\mathrm{jawaban}\:\mathrm{no}\:\mathrm{2}\right). \\ $$$$\mathrm{F}_{\mathrm{1},\mathrm{2}} =\mathrm{k}×\frac{\mathrm{q}_{\mathrm{1}} ×\mathrm{q}_{\mathrm{2}} }{\mathrm{r}^{\mathrm{2}} }\:\: \\ $$$$\mathrm{r}^{\mathrm{2}} =\frac{\mathrm{k}×\mathrm{q}_{\mathrm{1}} ×\mathrm{q}_{\mathrm{2}} }{\mathrm{F}_{\mathrm{1},\mathrm{2}} }\:=\frac{\mathrm{9}×\mathrm{10}^{\mathrm{9}} ×\mathrm{3}×\mathrm{10}^{−\mathrm{9}} ×\mathrm{12}×\mathrm{10}^{−\mathrm{9}} }{\mathrm{81}×\mathrm{10}^{−\mathrm{3}} } \\ $$$$=\frac{\mathrm{9}×\mathrm{3}×\mathrm{12}}{\mathrm{81}}×\mathrm{10}^{−\mathrm{6}} \:\mathrm{m}^{\mathrm{2}} \\ $$$$=\mathrm{4}×\mathrm{10}^{−\mathrm{6}} \:\mathrm{m}^{\mathrm{2}} \\ $$$$\mathrm{r}=\sqrt{\mathrm{4}×\mathrm{10}^{−\mathrm{6}} \:}\:=\mathrm{2}×\mathrm{10}^{−\mathrm{3}} \:\mathrm{m}=\mathrm{0},\mathrm{2}\:\mathrm{cm}// \\ $$
Answered by DELETED last updated on 12/Sep/21
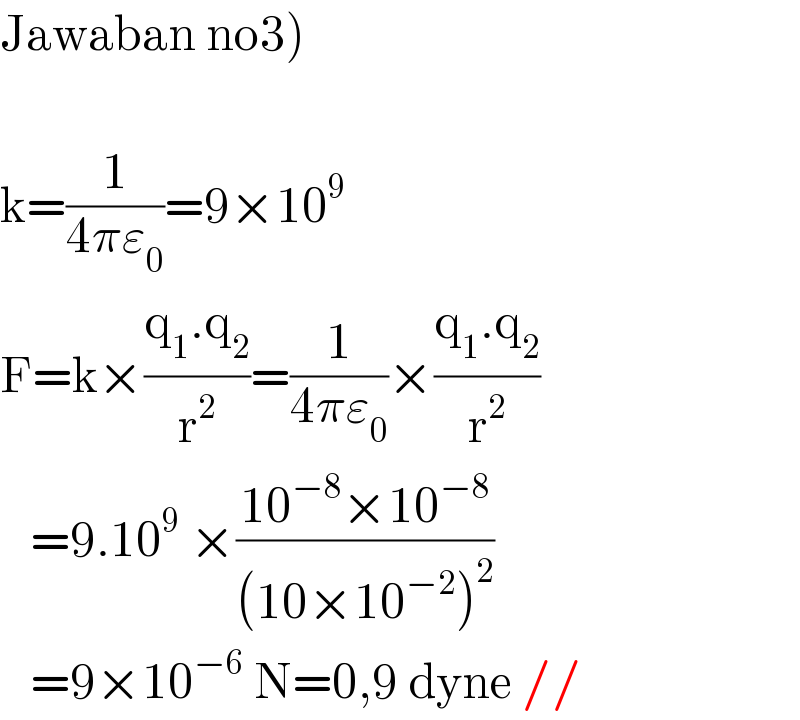
Jawaban no3) k=(1/(4πε_0 ))=9×10^9 F=k×((q_1 .q_2 )/r^2 )=(1/(4πε_0 ))×((q_1 .q_2 )/r^2 ) =9.10^9 ×((10^(−8) ×10^(−8) )/((10×10^(−2) )^2 )) =9×10^(−6) N=0,9 dyne //
$$\left.\mathrm{Jawaban}\:\mathrm{no3}\right) \\ $$$$ \\ $$$$\mathrm{k}=\frac{\mathrm{1}}{\mathrm{4}\pi\varepsilon_{\mathrm{0}} }=\mathrm{9}×\mathrm{10}^{\mathrm{9}} \: \\ $$$$\mathrm{F}=\mathrm{k}×\frac{\mathrm{q}_{\mathrm{1}} .\mathrm{q}_{\mathrm{2}} }{\mathrm{r}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{4}\pi\varepsilon_{\mathrm{0}} }×\frac{\mathrm{q}_{\mathrm{1}} .\mathrm{q}_{\mathrm{2}} }{\mathrm{r}^{\mathrm{2}} } \\ $$$$\:\:\:=\mathrm{9}.\mathrm{10}^{\mathrm{9}} \:×\frac{\mathrm{10}^{−\mathrm{8}} ×\mathrm{10}^{−\mathrm{8}} }{\left(\mathrm{10}×\mathrm{10}^{−\mathrm{2}} \right)^{\mathrm{2}} }\: \\ $$$$\:\:\:=\mathrm{9}×\mathrm{10}^{−\mathrm{6}} \:\mathrm{N}=\mathrm{0},\mathrm{9}\:\mathrm{dyne}\:// \\ $$
Answered by DELETED last updated on 12/Sep/21
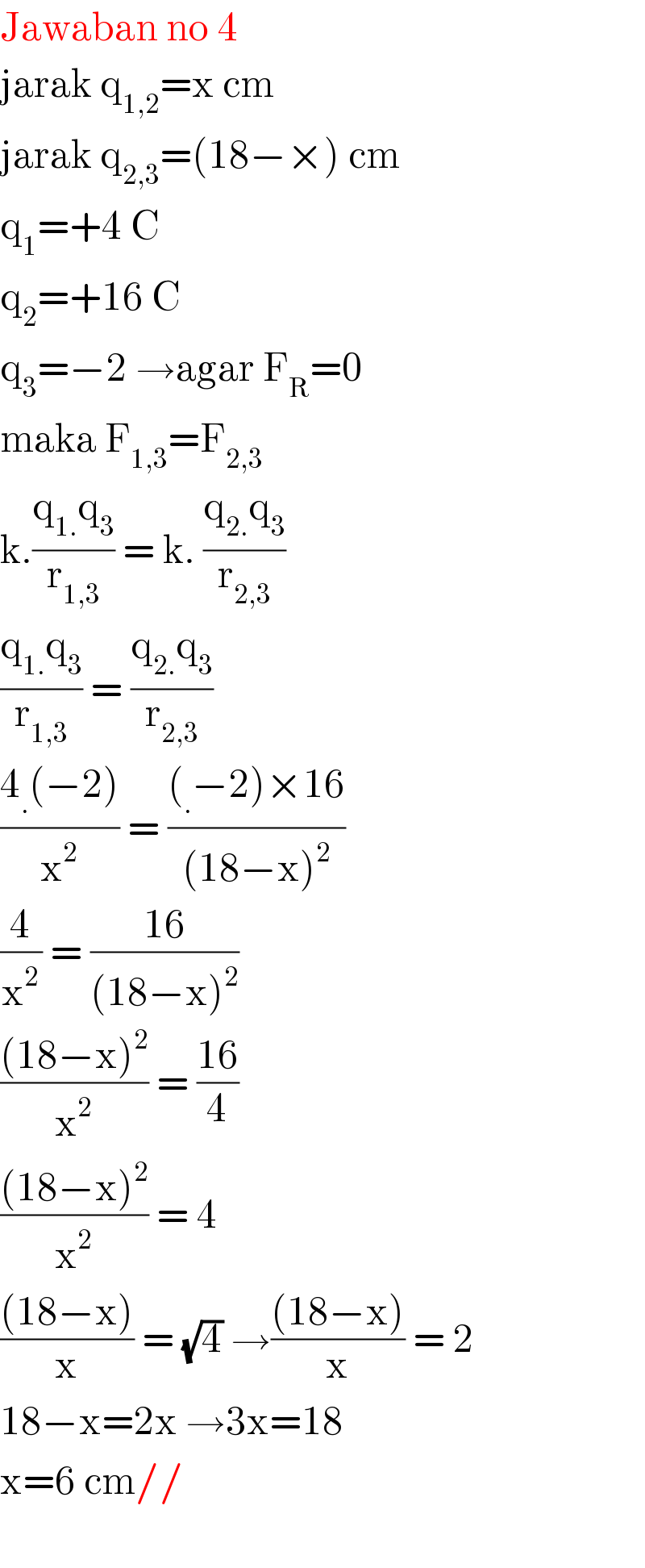
Jawaban no 4 jarak q_(1,2) =x cm jarak q_(2,3) =(18−×) cm q_1 =+4 C q_2 =+16 C q_3 =−2 →agar F_R =0 maka F_(1,3) =F_(2,3) k.((q_(1.) q_3 )/r_(1,3) ) = k. ((q_(2.) q_3 )/r_(2,3) ) ((q_(1.) q_3 )/r_(1,3) ) = ((q_(2.) q_3 )/r_(2,3) ) ((4_. (−2))/x^2 ) = (((_. −2)×16)/((18−x)^2 )) (4/x^2 ) = ((16)/((18−x)^2 )) (((18−x)^2 )/x^2 ) = ((16)/4) (((18−x)^2 )/x^2 ) = 4 (((18−x))/x) = (√4) →(((18−x))/x) = 2 18−x=2x →3x=18 x=6 cm//
$$\mathrm{Jawaban}\:\mathrm{no}\:\mathrm{4} \\ $$$$\mathrm{jarak}\:\mathrm{q}_{\mathrm{1},\mathrm{2}} =\mathrm{x}\:\mathrm{cm} \\ $$$$\mathrm{jarak}\:\mathrm{q}_{\mathrm{2},\mathrm{3}} =\left(\mathrm{18}−×\right)\:\mathrm{cm} \\ $$$$\mathrm{q}_{\mathrm{1}} =+\mathrm{4}\:\mathrm{C} \\ $$$$\mathrm{q}_{\mathrm{2}} =+\mathrm{16}\:\mathrm{C} \\ $$$$\mathrm{q}_{\mathrm{3}} =−\mathrm{2}\:\rightarrow\mathrm{agar}\:\mathrm{F}_{\mathrm{R}} =\mathrm{0} \\ $$$$\mathrm{maka}\:\mathrm{F}_{\mathrm{1},\mathrm{3}} =\mathrm{F}_{\mathrm{2},\mathrm{3}} \\ $$$$\mathrm{k}.\frac{\mathrm{q}_{\mathrm{1}.} \mathrm{q}_{\mathrm{3}} }{\mathrm{r}_{\mathrm{1},\mathrm{3}} }\:=\:\mathrm{k}.\:\frac{\mathrm{q}_{\mathrm{2}.} \mathrm{q}_{\mathrm{3}} }{\mathrm{r}_{\mathrm{2},\mathrm{3}} }\: \\ $$$$\frac{\mathrm{q}_{\mathrm{1}.} \mathrm{q}_{\mathrm{3}} }{\mathrm{r}_{\mathrm{1},\mathrm{3}} }\:=\:\frac{\mathrm{q}_{\mathrm{2}.} \mathrm{q}_{\mathrm{3}} }{\mathrm{r}_{\mathrm{2},\mathrm{3}} }\: \\ $$$$\frac{\mathrm{4}_{.} \left(−\mathrm{2}\right)}{\mathrm{x}^{\mathrm{2}} }\:=\:\frac{\left(_{.} −\mathrm{2}\right)×\mathrm{16}}{\left(\mathrm{18}−\mathrm{x}\right)^{\mathrm{2}} }\: \\ $$$$\frac{\mathrm{4}}{\mathrm{x}^{\mathrm{2}} }\:=\:\frac{\mathrm{16}}{\left(\mathrm{18}−\mathrm{x}\right)^{\mathrm{2}} }\: \\ $$$$\frac{\left(\mathrm{18}−\mathrm{x}\right)^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} }\:=\:\frac{\mathrm{16}}{\mathrm{4}}\: \\ $$$$\frac{\left(\mathrm{18}−\mathrm{x}\right)^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} }\:=\:\mathrm{4} \\ $$$$\frac{\left(\mathrm{18}−\mathrm{x}\right)}{\mathrm{x}}\:=\:\sqrt{\mathrm{4}}\:\rightarrow\frac{\left(\mathrm{18}−\mathrm{x}\right)}{\mathrm{x}}\:=\:\mathrm{2} \\ $$$$\mathrm{18}−\mathrm{x}=\mathrm{2x}\:\rightarrow\mathrm{3x}=\mathrm{18} \\ $$$$\mathrm{x}=\mathrm{6}\:\mathrm{cm}// \\ $$$$ \\ $$
Answered by DELETED last updated on 12/Sep/21
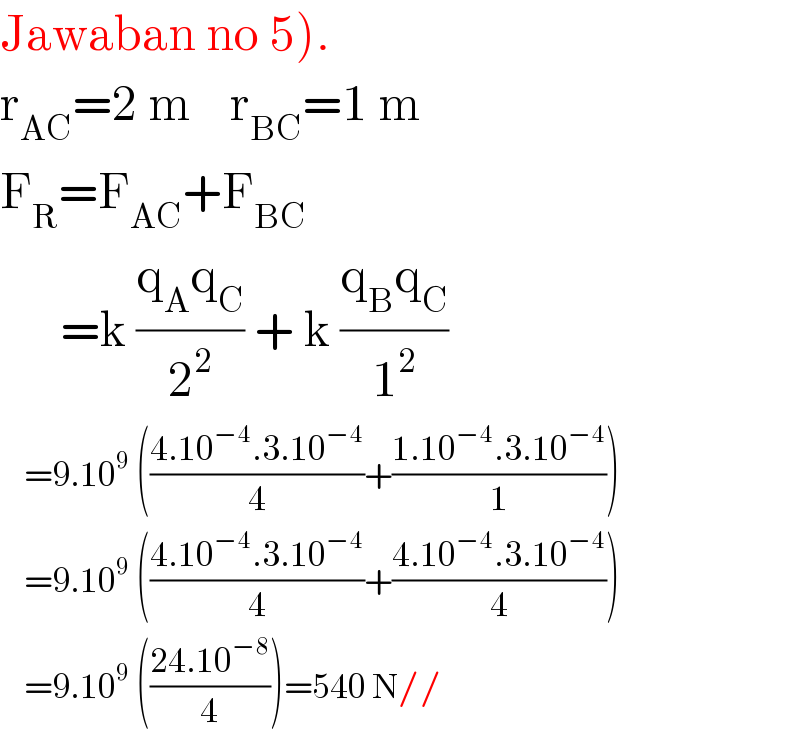
Jawaban no 5). r_(AC) =2 m r_(BC) =1 m F_R =F_(AC) +F_(BC) =k ((q_A q_C )/2^2 ) + k ((q_B q_C )/1^2 ) =9.10^9 (((4.10^(−4) .3.10^(−4) )/4)+((1.10^(−4) .3.10^(−4) )/1)) =9.10^9 (((4.10^(−4) .3.10^(−4) )/4)+((4.10^(−4) .3.10^(−4) )/4)) =9.10^9 (((24.10^(−8) )/4))=540 N//
$$\left.\mathrm{Jawaban}\:\mathrm{no}\:\mathrm{5}\right). \\ $$$$\mathrm{r}_{\mathrm{AC}} =\mathrm{2}\:\mathrm{m}\:\:\:\:\mathrm{r}_{\mathrm{BC}} =\mathrm{1}\:\mathrm{m} \\ $$$$\mathrm{F}_{\mathrm{R}} =\mathrm{F}_{\mathrm{AC}} +\mathrm{F}_{\mathrm{BC}} \\ $$$$\:\:\:\:\:\:=\mathrm{k}\:\frac{\mathrm{q}_{\mathrm{A}} \mathrm{q}_{\mathrm{C}} }{\mathrm{2}^{\mathrm{2}} }\:+\:\mathrm{k}\:\frac{\mathrm{q}_{\mathrm{B}} \mathrm{q}_{\mathrm{C}} }{\mathrm{1}^{\mathrm{2}} } \\ $$$$\:\:\:\:=\mathrm{9}.\mathrm{10}^{\mathrm{9}} \:\left(\frac{\mathrm{4}.\mathrm{10}^{−\mathrm{4}} .\mathrm{3}.\mathrm{10}^{−\mathrm{4}} }{\mathrm{4}}+\frac{\mathrm{1}.\mathrm{10}^{−\mathrm{4}} .\mathrm{3}.\mathrm{10}^{−\mathrm{4}} }{\mathrm{1}}\right) \\ $$$$\:\:\:\:=\mathrm{9}.\mathrm{10}^{\mathrm{9}} \:\left(\frac{\mathrm{4}.\mathrm{10}^{−\mathrm{4}} .\mathrm{3}.\mathrm{10}^{−\mathrm{4}} }{\mathrm{4}}+\frac{\mathrm{4}.\mathrm{10}^{−\mathrm{4}} .\mathrm{3}.\mathrm{10}^{−\mathrm{4}} }{\mathrm{4}}\right) \\ $$$$\:\:\:\:=\mathrm{9}.\mathrm{10}^{\mathrm{9}} \:\left(\frac{\mathrm{24}.\mathrm{10}^{−\mathrm{8}} }{\mathrm{4}}\right)=\mathrm{540}\:\mathrm{N}// \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *