Question Number 153977 by mr W last updated on 12/Sep/21
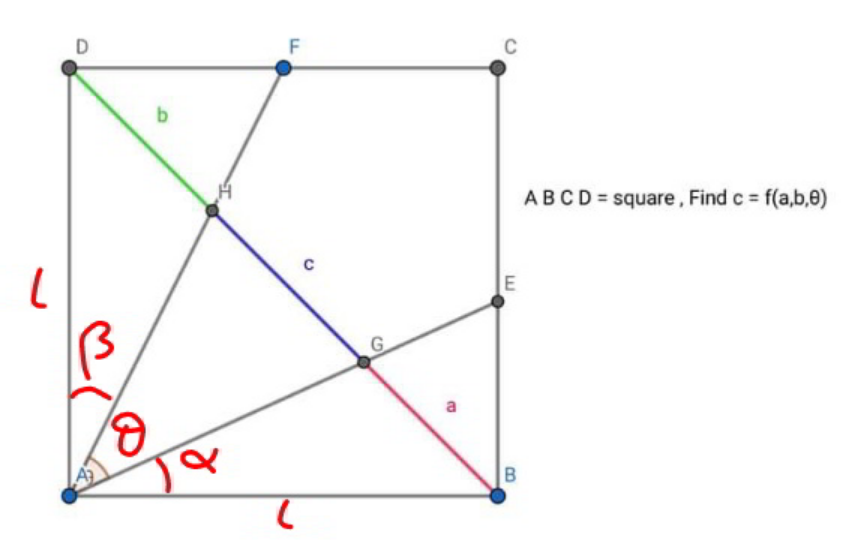
Answered by mr W last updated on 12/Sep/21
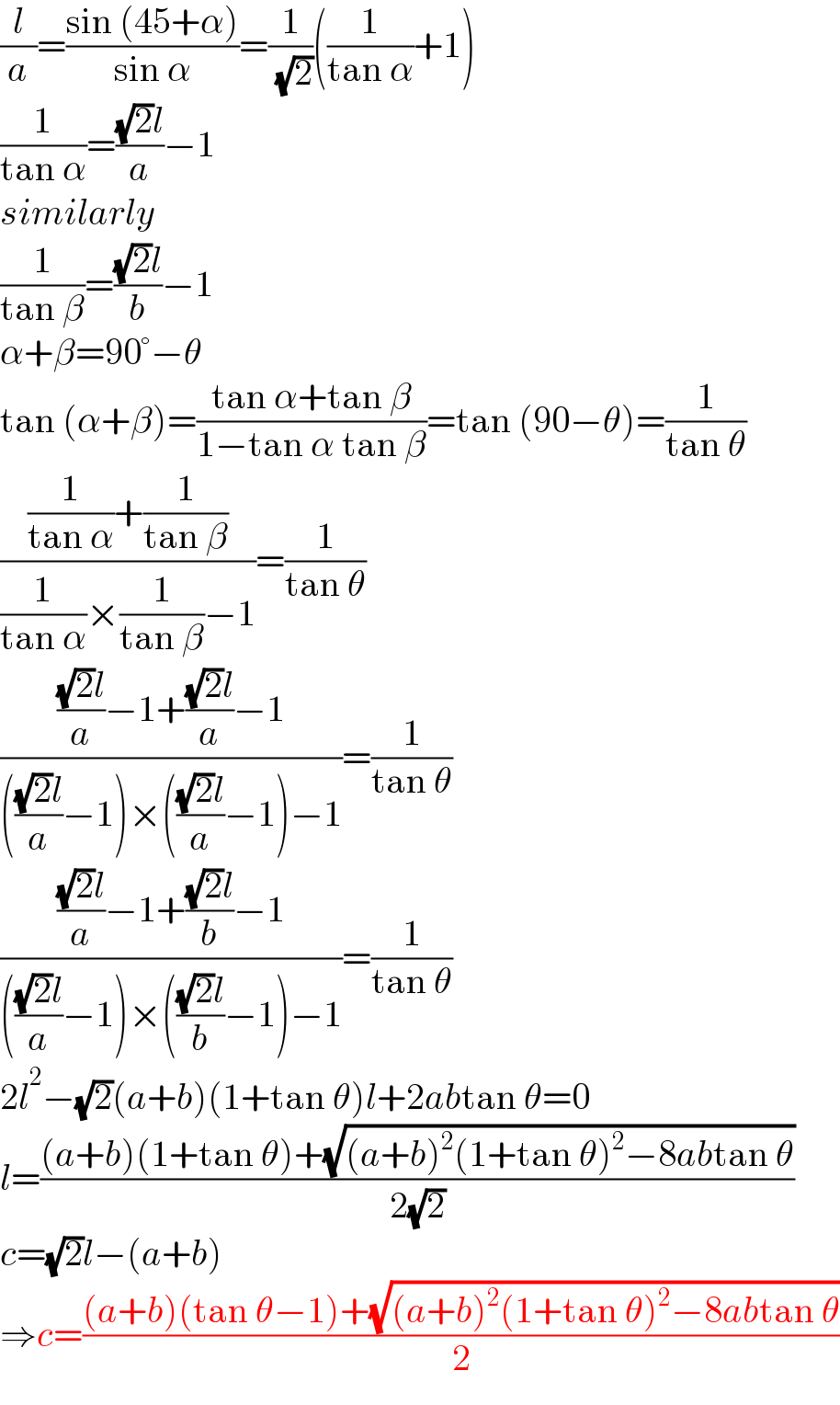
$$\frac{{l}}{{a}}=\frac{\mathrm{sin}\:\left(\mathrm{45}+\alpha\right)}{\mathrm{sin}\:\alpha}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left(\frac{\mathrm{1}}{\mathrm{tan}\:\alpha}+\mathrm{1}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{tan}\:\alpha}=\frac{\sqrt{\mathrm{2}}{l}}{{a}}−\mathrm{1} \\ $$$${similarly} \\ $$$$\frac{\mathrm{1}}{\mathrm{tan}\:\beta}=\frac{\sqrt{\mathrm{2}}{l}}{{b}}−\mathrm{1} \\ $$$$\alpha+\beta=\mathrm{90}°−\theta \\ $$$$\mathrm{tan}\:\left(\alpha+\beta\right)=\frac{\mathrm{tan}\:\alpha+\mathrm{tan}\:\beta}{\mathrm{1}−\mathrm{tan}\:\alpha\:\mathrm{tan}\:\beta}=\mathrm{tan}\:\left(\mathrm{90}−\theta\right)=\frac{\mathrm{1}}{\mathrm{tan}\:\theta} \\ $$$$\frac{\frac{\mathrm{1}}{\mathrm{tan}\:\alpha}+\frac{\mathrm{1}}{\mathrm{tan}\:\beta}}{\frac{\mathrm{1}}{\mathrm{tan}\:\alpha}×\frac{\mathrm{1}}{\mathrm{tan}\:\beta}−\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{tan}\:\theta} \\ $$$$\frac{\frac{\sqrt{\mathrm{2}}{l}}{{a}}−\mathrm{1}+\frac{\sqrt{\mathrm{2}}{l}}{{a}}−\mathrm{1}}{\left(\frac{\sqrt{\mathrm{2}}{l}}{{a}}−\mathrm{1}\right)×\left(\frac{\sqrt{\mathrm{2}}{l}}{{a}}−\mathrm{1}\right)−\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{tan}\:\theta} \\ $$$$\frac{\frac{\sqrt{\mathrm{2}}{l}}{{a}}−\mathrm{1}+\frac{\sqrt{\mathrm{2}}{l}}{{b}}−\mathrm{1}}{\left(\frac{\sqrt{\mathrm{2}}{l}}{{a}}−\mathrm{1}\right)×\left(\frac{\sqrt{\mathrm{2}}{l}}{{b}}−\mathrm{1}\right)−\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{tan}\:\theta} \\ $$$$\mathrm{2}{l}^{\mathrm{2}} −\sqrt{\mathrm{2}}\left({a}+{b}\right)\left(\mathrm{1}+\mathrm{tan}\:\theta\right){l}+\mathrm{2}{ab}\mathrm{tan}\:\theta=\mathrm{0} \\ $$$${l}=\frac{\left({a}+{b}\right)\left(\mathrm{1}+\mathrm{tan}\:\theta\right)+\sqrt{\left({a}+{b}\right)^{\mathrm{2}} \left(\mathrm{1}+\mathrm{tan}\:\theta\right)^{\mathrm{2}} −\mathrm{8}{ab}\mathrm{tan}\:\theta}}{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$${c}=\sqrt{\mathrm{2}}{l}−\left({a}+{b}\right) \\ $$$$\Rightarrow{c}=\frac{\left({a}+{b}\right)\left(\mathrm{tan}\:\theta−\mathrm{1}\right)+\sqrt{\left({a}+{b}\right)^{\mathrm{2}} \left(\mathrm{1}+\mathrm{tan}\:\theta\right)^{\mathrm{2}} −\mathrm{8}{ab}\mathrm{tan}\:\theta}}{\mathrm{2}} \\ $$
Commented by Tawa11 last updated on 12/Sep/21

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Commented by liberty last updated on 13/Sep/21

$${waw} \\ $$
