Question Number 154058 by mnjuly1970 last updated on 13/Sep/21

Answered by qaz last updated on 14/Sep/21
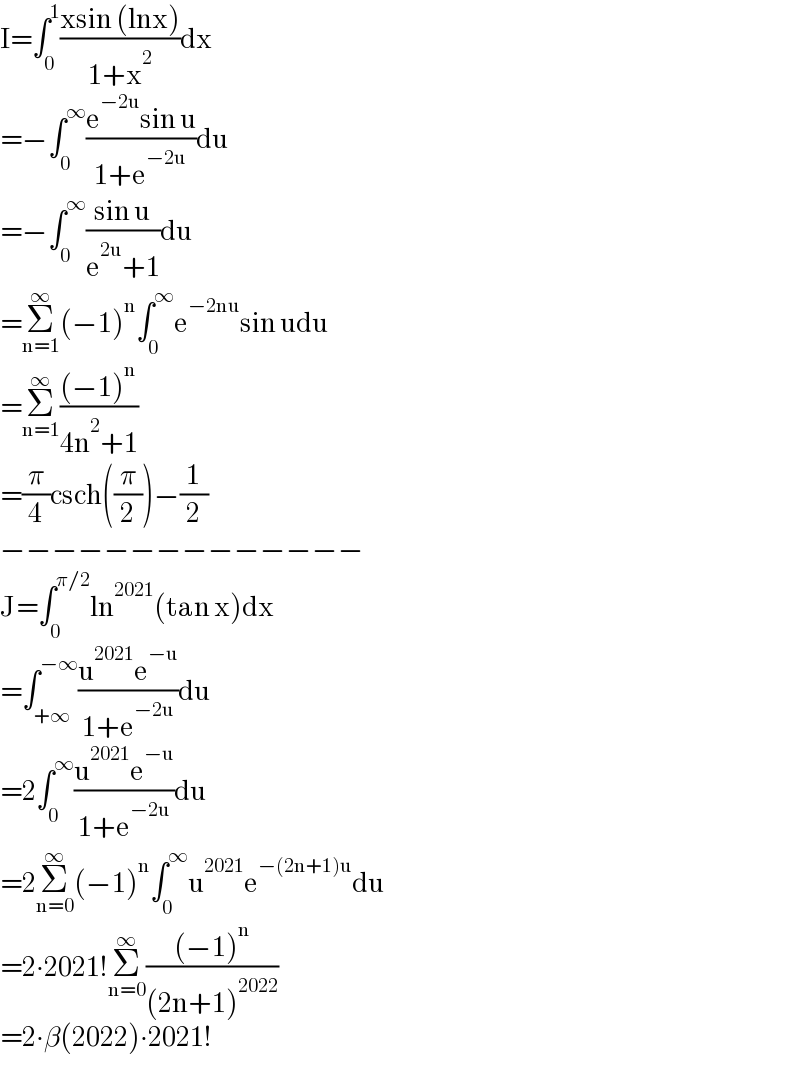
$$\mathrm{I}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{xsin}\:\left(\mathrm{lnx}\right)}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx} \\ $$$$=−\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{e}^{−\mathrm{2u}} \mathrm{sin}\:\mathrm{u}}{\mathrm{1}+\mathrm{e}^{−\mathrm{2u}} }\mathrm{du} \\ $$$$=−\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{sin}\:\mathrm{u}}{\mathrm{e}^{\mathrm{2u}} +\mathrm{1}}\mathrm{du} \\ $$$$=\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{\mathrm{n}} \int_{\mathrm{0}} ^{\infty} \mathrm{e}^{−\mathrm{2nu}} \mathrm{sin}\:\mathrm{udu} \\ $$$$=\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{4n}^{\mathrm{2}} +\mathrm{1}} \\ $$$$=\frac{\pi}{\mathrm{4}}\mathrm{csch}\left(\frac{\pi}{\mathrm{2}}\right)−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$−−−−−−−−−−−−−− \\ $$$$\mathrm{J}=\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \mathrm{ln}^{\mathrm{2021}} \left(\mathrm{tan}\:\mathrm{x}\right)\mathrm{dx} \\ $$$$=\int_{+\infty} ^{−\infty} \frac{\mathrm{u}^{\mathrm{2021}} \mathrm{e}^{−\mathrm{u}} }{\mathrm{1}+\mathrm{e}^{−\mathrm{2u}} }\mathrm{du} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{u}^{\mathrm{2021}} \mathrm{e}^{−\mathrm{u}} }{\mathrm{1}+\mathrm{e}^{−\mathrm{2u}} }\mathrm{du} \\ $$$$=\mathrm{2}\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{\mathrm{n}} \int_{\mathrm{0}} ^{\infty} \mathrm{u}^{\mathrm{2021}} \mathrm{e}^{−\left(\mathrm{2n}+\mathrm{1}\right)\mathrm{u}} \mathrm{du} \\ $$$$=\mathrm{2}\centerdot\mathrm{2021}!\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{2022}} } \\ $$$$=\mathrm{2}\centerdot\beta\left(\mathrm{2022}\right)\centerdot\mathrm{2021}! \\ $$
