Question Number 154085 by iloveisrael last updated on 14/Sep/21

Commented by iloveisrael last updated on 14/Sep/21
$${find}\:{area}\:{of}\:{triangle}\:{ABC} \\ $$
Answered by EDWIN88 last updated on 14/Sep/21
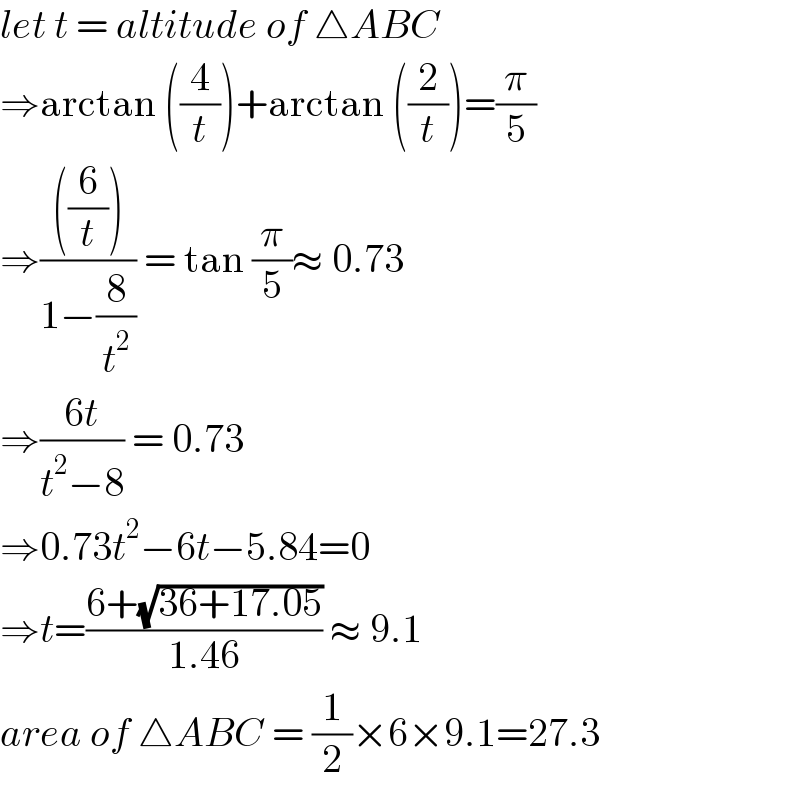
$${let}\:{t}\:=\:{altitude}\:{of}\:\bigtriangleup{ABC} \\ $$$$\Rightarrow\mathrm{arctan}\:\left(\frac{\mathrm{4}}{{t}}\right)+\mathrm{arctan}\:\left(\frac{\mathrm{2}}{{t}}\right)=\frac{\pi}{\mathrm{5}} \\ $$$$\Rightarrow\frac{\left(\frac{\mathrm{6}}{{t}}\right)}{\mathrm{1}−\frac{\mathrm{8}}{{t}^{\mathrm{2}} }}\:=\:\mathrm{tan}\:\frac{\pi}{\mathrm{5}}\approx\:\mathrm{0}.\mathrm{73} \\ $$$$\Rightarrow\frac{\mathrm{6}{t}}{{t}^{\mathrm{2}} −\mathrm{8}}\:=\:\mathrm{0}.\mathrm{73}\: \\ $$$$\Rightarrow\mathrm{0}.\mathrm{73}{t}^{\mathrm{2}} −\mathrm{6}{t}−\mathrm{5}.\mathrm{84}=\mathrm{0} \\ $$$$\Rightarrow{t}=\frac{\mathrm{6}+\sqrt{\mathrm{36}+\mathrm{17}.\mathrm{05}}}{\mathrm{1}.\mathrm{46}}\:\approx\:\mathrm{9}.\mathrm{1} \\ $$$${area}\:{of}\:\bigtriangleup{ABC}\:=\:\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{6}×\mathrm{9}.\mathrm{1}=\mathrm{27}.\mathrm{3} \\ $$
