Question-154142

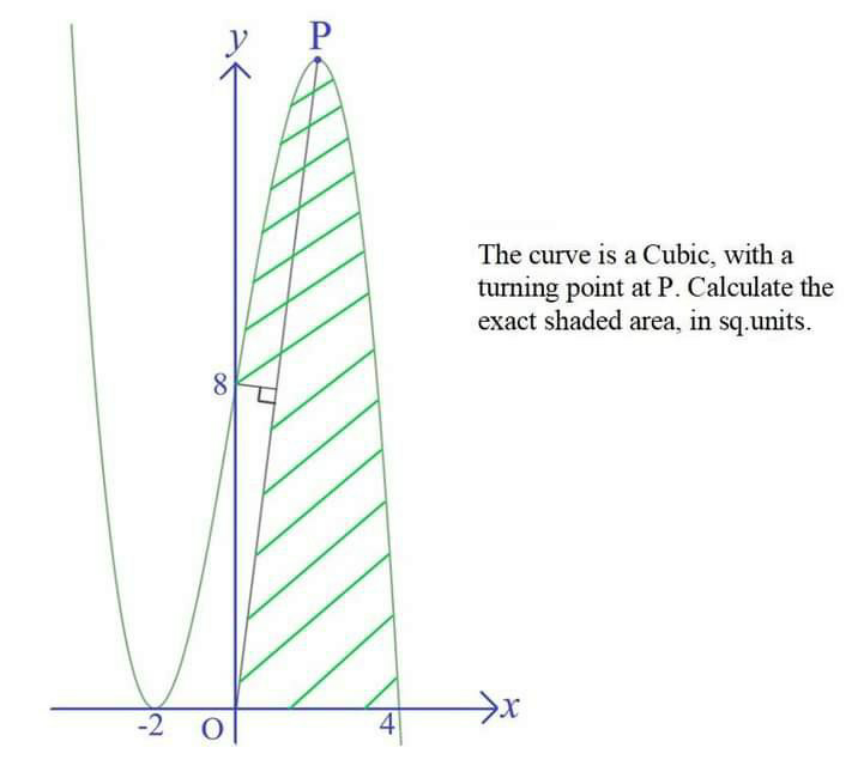
Question Number 154142 by EDWIN88 last updated on 14/Sep/21

Answered by mr W last updated on 14/Sep/21

y = a (x - 4) {(x + 2)}^{2}

8 = a (- 4) {(+ 2)}^{2} \Rightarrow a = - \frac{1}{2}

y = - \frac{1}{2} (x - 4) {(x + 2)}^{2}

\frac{d y}{d x} = - \frac{1}{2} [{(x + 2)}^{2} + 2 (x - 4) (x + 2)] = 0

(x + 2) (x - 2) = 0

\Rightarrow x = - 2 (r e j e c t e d)

\Rightarrow x = 2 \Rightarrow x_{P} = 2, y_{P} = - \frac{1}{2} (2 - 4) {(2 + 2)}^{2} = 16

e q n . o f O P :

y = 8 x

e q n . o f Q R :

y = 8 - \frac{x}{8}

8 - \frac{x}{8} = 8 x \Rightarrow x_{R} = \frac{64}{65}

A = \int_{0}^{4} y d x - \frac{1}{2} \times 8 \times \frac{64}{65}

A = - \frac{1}{2} \int_{0}^{4} (x - 4) {(x + 2)}^{2} d x - \frac{256}{65}

A = - \frac{1}{2} \int_{0}^{4} (x^{3} - 12 x - 16) d x - \frac{256}{65}

A = - \frac{1}{2} [\frac{4^{4}}{4} - 6 \times 4^{2} - 16 \times 4] - \frac{256}{65}

A = 48 - \frac{256}{65} = \frac{2864}{65} \approx 44.06

Commented by iloveisrael last updated on 15/Sep/21

y e s

Answered by iloveisrael last updated on 15/Sep/21