Question Number 154175 by daus last updated on 15/Sep/21
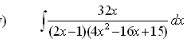
Commented by daus last updated on 15/Sep/21
integrate it
Answered by EDWIN88 last updated on 15/Sep/21
![∫ ((32x)/((2x−1)(2x −3 )(2x−5))) dx ((32x)/((2x−1)(2x−3)(2x−5)))=(a/(2x−1))+(b/(2x−3))+(c/(2x−5)) a=[((32x)/((2x−3)(2x−5)))] _(x=(1/2)) =((16)/((−2)(−4)))=2 b=[((32x)/((2x−1)(2x−5)))]_(x=(3/2)) =((48)/((2)(−2)))=−12 c= [((32x)/((2x−1)(2x−3)))]_(x=(5/2)) =((80)/((4)(2)))=10 I=∫ (2/(2x−1)) dx−∫ ((12)/(2x−3)) dx +∫ ((10)/(2x−5)) dx I=ln ∣2x−1∣−6ln ∣2x−3∣+5ln ∣2x−5∣ + c I=ln ∣((C(2x−1)(2x−5)^5 )/((2x−3)^6 ))∣ .](https://www.tinkutara.com/question/Q154179.png)
$$\int\:\frac{\mathrm{32}{x}}{\left(\mathrm{2}{x}−\mathrm{1}\right)\left(\mathrm{2}{x}\:−\mathrm{3}\:\:\right)\left(\mathrm{2}{x}−\mathrm{5}\right)}\:{dx} \\ $$$$\:\frac{\mathrm{32}{x}}{\left(\mathrm{2}{x}−\mathrm{1}\right)\left(\mathrm{2}{x}−\mathrm{3}\right)\left(\mathrm{2}{x}−\mathrm{5}\right)}=\frac{{a}}{\mathrm{2}{x}−\mathrm{1}}+\frac{{b}}{\mathrm{2}{x}−\mathrm{3}}+\frac{{c}}{\mathrm{2}{x}−\mathrm{5}} \\ $$$$\:{a}=\left[\frac{\mathrm{32}{x}}{\left(\mathrm{2}{x}−\mathrm{3}\right)\left(\mathrm{2}{x}−\mathrm{5}\right)}\right]\:_{{x}=\frac{\mathrm{1}}{\mathrm{2}}} =\frac{\mathrm{16}}{\left(−\mathrm{2}\right)\left(−\mathrm{4}\right)}=\mathrm{2} \\ $$$$\:{b}=\left[\frac{\mathrm{32}{x}}{\left(\mathrm{2}{x}−\mathrm{1}\right)\left(\mathrm{2}{x}−\mathrm{5}\right)}\right]_{{x}=\frac{\mathrm{3}}{\mathrm{2}}} =\frac{\mathrm{48}}{\left(\mathrm{2}\right)\left(−\mathrm{2}\right)}=−\mathrm{12} \\ $$$$\:{c}=\:\left[\frac{\mathrm{32}{x}}{\left(\mathrm{2}{x}−\mathrm{1}\right)\left(\mathrm{2}{x}−\mathrm{3}\right)}\right]_{{x}=\frac{\mathrm{5}}{\mathrm{2}}} =\frac{\mathrm{80}}{\left(\mathrm{4}\right)\left(\mathrm{2}\right)}=\mathrm{10} \\ $$$${I}=\int\:\frac{\mathrm{2}}{\mathrm{2}{x}−\mathrm{1}}\:{dx}−\int\:\frac{\mathrm{12}}{\mathrm{2}{x}−\mathrm{3}}\:{dx}\:+\int\:\frac{\mathrm{10}}{\mathrm{2}{x}−\mathrm{5}}\:{dx} \\ $$$${I}=\mathrm{ln}\:\mid\mathrm{2}{x}−\mathrm{1}\mid−\mathrm{6ln}\:\mid\mathrm{2}{x}−\mathrm{3}\mid+\mathrm{5ln}\:\mid\mathrm{2}{x}−\mathrm{5}\mid\:+\:{c} \\ $$$${I}=\mathrm{ln}\:\mid\frac{{C}\left(\mathrm{2}{x}−\mathrm{1}\right)\left(\mathrm{2}{x}−\mathrm{5}\right)^{\mathrm{5}} }{\left(\mathrm{2}{x}−\mathrm{3}\right)^{\mathrm{6}} }\mid\:. \\ $$
Commented by daus last updated on 15/Sep/21
appreaciated
Answered by peter frank last updated on 15/Sep/21

