Question Number 154177 by EDWIN88 last updated on 15/Sep/21

Commented by Tawa11 last updated on 15/Sep/21

$$\mathrm{nice} \\ $$
Commented by EDWIN88 last updated on 16/Sep/21
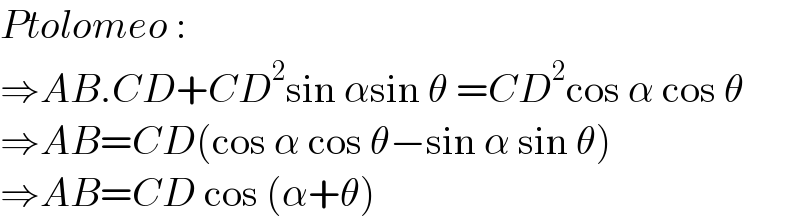
$${Ptolomeo}\:: \\ $$$$\Rightarrow{AB}.{CD}+{CD}^{\mathrm{2}} \mathrm{sin}\:\alpha\mathrm{sin}\:\theta\:={CD}^{\mathrm{2}} \mathrm{cos}\:\alpha\:\mathrm{cos}\:\theta \\ $$$$\Rightarrow{AB}={CD}\left(\mathrm{cos}\:\alpha\:\mathrm{cos}\:\theta−\mathrm{sin}\:\alpha\:\mathrm{sin}\:\theta\right) \\ $$$$\Rightarrow{AB}={CD}\:\mathrm{cos}\:\left(\alpha+\theta\right) \\ $$
Answered by som(math1967) last updated on 15/Sep/21

Commented by som(math1967) last updated on 15/Sep/21
![let o is centre ∴CO=AO=BO=((CD)/2) ∡BCO=∡OBC=𝛉 [CO=BO] ∴∡ABO=∡BAO=𝛂+𝛉 ∡AOB=180−2(𝛂+𝛉) from △AOB ((AB)/(Sin(180−2𝛂−2θ)))=((AO)/(Sin(𝛂+𝛉))) ((AB)/(Sin2(𝛂+𝛉)))=((AO)/(sin(𝛂+𝛉))) ((AB)/(2sin(𝛂+θ)cos(𝛂+𝛉)))=((AO)/(sin(𝛂+𝛉))) AB=2AOcos(𝛂+𝛉) AB=CDcos(𝛂+𝛉) [proved]](https://www.tinkutara.com/question/Q154183.png)
$$\boldsymbol{{let}}\:\boldsymbol{{o}}\:\boldsymbol{{is}}\:\boldsymbol{{centre}}\:\therefore\boldsymbol{{CO}}=\boldsymbol{{AO}}=\boldsymbol{{BO}}=\frac{\boldsymbol{{CD}}}{\mathrm{2}} \\ $$$$\measuredangle\boldsymbol{{BCO}}=\measuredangle\boldsymbol{{OBC}}=\boldsymbol{\theta}\:\:\left[\boldsymbol{{CO}}=\boldsymbol{{BO}}\right] \\ $$$$\therefore\measuredangle\boldsymbol{{ABO}}=\measuredangle\boldsymbol{{B}}{AO}=\boldsymbol{\alpha}+\boldsymbol{\theta} \\ $$$$\measuredangle\boldsymbol{{AOB}}=\mathrm{180}−\mathrm{2}\left(\boldsymbol{\alpha}+\boldsymbol{\theta}\right) \\ $$$$\boldsymbol{{from}}\:\bigtriangleup\boldsymbol{{AOB}} \\ $$$$\:\:\frac{\boldsymbol{{AB}}}{\boldsymbol{{Sin}}\left(\mathrm{180}−\mathrm{2}\boldsymbol{\alpha}−\mathrm{2}\theta\right)}=\frac{\boldsymbol{{AO}}}{\boldsymbol{{Sin}}\left(\boldsymbol{\alpha}+\boldsymbol{\theta}\right)} \\ $$$$\frac{\boldsymbol{{AB}}}{\boldsymbol{{Sin}}\mathrm{2}\left(\boldsymbol{\alpha}+\boldsymbol{\theta}\right)}=\frac{\boldsymbol{{AO}}}{\boldsymbol{{sin}}\left(\boldsymbol{\alpha}+\boldsymbol{\theta}\right)} \\ $$$$\frac{\boldsymbol{{A}}{B}}{\mathrm{2}\boldsymbol{{sin}}\left(\boldsymbol{\alpha}+\theta\right){c}\boldsymbol{{os}}\left(\boldsymbol{\alpha}+\boldsymbol{\theta}\right)}=\frac{\boldsymbol{{A}}{O}}{\boldsymbol{{sin}}\left(\boldsymbol{\alpha}+\boldsymbol{\theta}\right)} \\ $$$$\boldsymbol{{AB}}=\mathrm{2}\boldsymbol{{AOcos}}\left(\boldsymbol{\alpha}+\boldsymbol{\theta}\right) \\ $$$$\boldsymbol{{AB}}=\boldsymbol{{CDcos}}\left(\boldsymbol{\alpha}+\boldsymbol{\theta}\right)\:\:\:\left[\boldsymbol{{proved}}\right] \\ $$
Commented by mr W last updated on 15/Sep/21
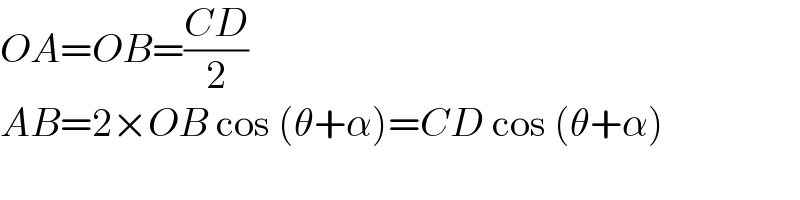
$${OA}={OB}=\frac{{CD}}{\mathrm{2}} \\ $$$${AB}=\mathrm{2}×{OB}\:\mathrm{cos}\:\left(\theta+\alpha\right)={CD}\:\mathrm{cos}\:\left(\theta+\alpha\right) \\ $$
