Question-154204

Question Number 154204 by mathdanisur last updated on 15/Sep/21

Commented by Rasheed.Sindhi last updated on 16/Sep/21

Sorry that I neglect “ ((tanα )/(tanβ )) ∈Z^+ ”. Now the question can be solved for some fixed answers.

$$\boldsymbol{\mathrm{Sorry}}\:\mathrm{that}\:\mathrm{I}\:\mathrm{neglect}\:“\:\frac{\mathrm{tan}\alpha\:}{\mathrm{tan}\beta\:}\:\in\mathbb{Z}^{+} \:''. \\ $$$$\mathrm{Now}\:\mathrm{the}\:\mathrm{question}\:\mathrm{can}\:\mathrm{be}\:\mathrm{solved}\:\mathrm{for} \\ $$$$\mathrm{some}\:\mathrm{fixed}\:\mathrm{answers}. \\ $$

Answered by Rasheed.Sindhi last updated on 15/Sep/21

•△OA_1 C in which ∠COA_1 =α+β ((sin(α+β) )/2)=((sin∠OCA_1 )/1) C=sin^(−1) (((sin(α+β) )/2)) ∠A_n OB_2 =α+β+OCA_1 ∠A_n OB_2 =α+β+sin^(−1) (((sin(α+β) )/2)) ∠OA_1 C=π−(α+β+C) ∠OA_1 C=π−(α+β+sin^(−1) (((sin(α+β) )/2))) •△OA_n D in which ∠DOA_n =β ((sinβ )/1)=((sinD )/n) •△OA_1 E in which ∠EOA_1 =β ((sinβ )/(A_1 E))=((sinE )/(OA_1 )) ((sinβ )/(A_1 E))=((sinE )/1) •△OA_1 E∼△OA_n D ((OA_1 )/(OA_n ))=((A_1 E)/(A_n D)) (1/n)=((A_1 E)/1) n=(1/(A_1 E)) Continue

$$\:\bullet\bigtriangleup\mathrm{OA}_{\mathrm{1}} \mathrm{C}\:{in}\:{which}\:\angle\mathrm{COA}_{\mathrm{1}} =\alpha+\beta \\ $$$$\:\:\:\frac{\mathrm{sin}\left(\alpha+\beta\right)\:}{\mathrm{2}}=\frac{\mathrm{sin}\angle\mathrm{OCA}_{\mathrm{1}} \:}{\mathrm{1}} \\ $$$$\:\:\:\mathrm{C}=\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{sin}\left(\alpha+\beta\right)\:}{\mathrm{2}}\right) \\ $$$$\:\:\angle\mathrm{A}_{\mathrm{n}} \mathrm{OB}_{\mathrm{2}} =\alpha+\beta+\mathrm{OCA}_{\mathrm{1}} \\ $$$$\:\:\angle\mathrm{A}_{\mathrm{n}} \mathrm{OB}_{\mathrm{2}} =\alpha+\beta+\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{sin}\left(\alpha+\beta\right)\:}{\mathrm{2}}\right) \\ $$$$\angle\mathrm{OA}_{\mathrm{1}} \mathrm{C}=\pi−\left(\alpha+\beta+\mathrm{C}\right) \\ $$$$\angle\mathrm{OA}_{\mathrm{1}} \mathrm{C}=\pi−\left(\alpha+\beta+\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{sin}\left(\alpha+\beta\right)\:}{\mathrm{2}}\right)\right) \\ $$$$\bullet\bigtriangleup\mathrm{OA}_{\mathrm{n}} \mathrm{D}\:{in}\:{which}\:\angle\mathrm{DOA}_{\mathrm{n}} =\beta \\ $$$$\:\:\:\frac{\mathrm{sin}\beta\:}{\mathrm{1}}=\frac{\mathrm{sinD}\:}{\mathrm{n}} \\ $$$$\bullet\bigtriangleup\mathrm{OA}_{\mathrm{1}} \mathrm{E}\:{in}\:{which}\:\angle\mathrm{EOA}_{\mathrm{1}} =\beta \\ $$$$\frac{\mathrm{sin}\beta\:}{\mathrm{A}_{\mathrm{1}} \mathrm{E}}=\frac{\mathrm{sinE}\:}{\mathrm{OA}_{\mathrm{1}} } \\ $$$$\frac{\mathrm{sin}\beta\:}{\mathrm{A}_{\mathrm{1}} \mathrm{E}}=\frac{\mathrm{sinE}\:}{\mathrm{1}} \\ $$$$\bullet\bigtriangleup\mathrm{OA}_{\mathrm{1}} \mathrm{E}\sim\bigtriangleup\mathrm{OA}_{\mathrm{n}} \mathrm{D} \\ $$$$\frac{\mathrm{OA}_{\mathrm{1}} }{\mathrm{OA}_{\mathrm{n}} }=\frac{\mathrm{A}_{\mathrm{1}} \mathrm{E}}{\mathrm{A}_{\mathrm{n}} \mathrm{D}} \\ $$$$\frac{\mathrm{1}}{\mathrm{n}}=\frac{\mathrm{A}_{\mathrm{1}} \mathrm{E}}{\mathrm{1}} \\ $$$$\mathrm{n}=\frac{\mathrm{1}}{\mathrm{A}_{\mathrm{1}} \mathrm{E}} \\ $$$$\:\:\:\:\:\mathrm{Continue} \\ $$

Commented by mathdanisur last updated on 15/Sep/21

$$\boldsymbol{\mathrm{S}}\mathrm{er},\:\mathrm{ans}:\:\mathrm{n}=\mathrm{8}\:\mathrm{and}\:\mathrm{A}_{\mathrm{1}} \mathrm{OB}_{\mathrm{1}} =\mathrm{90}° \\ $$

Commented by Rasheed.Sindhi last updated on 15/Sep/21

I think that the answers depend upon the values of α & β.

$${I}\:{think}\:\:{that}\:{the}\:{answers}\:{depend} \\ $$$${upon}\:{the}\:{values}\:{of}\:\alpha\:\&\:\beta. \\ $$

Commented by mathdanisur last updated on 15/Sep/21

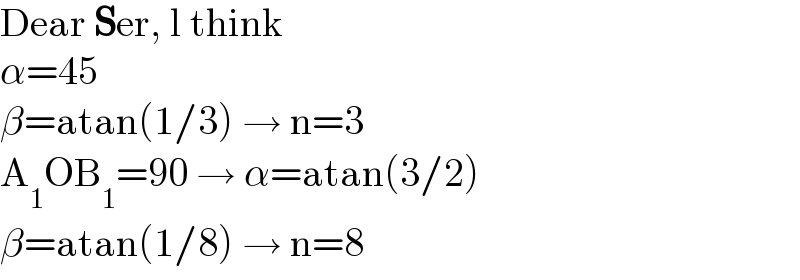
Dear Ser, l think α=45 β=atan(1/3) → n=3 A_1 OB_1 =90 → α=atan(3/2) β=atan(1/8) → n=8

$$\mathrm{Dear}\:\boldsymbol{\mathrm{S}}\mathrm{er},\:\mathrm{l}\:\mathrm{think} \\ $$$$\alpha=\mathrm{45} \\ $$$$\beta=\mathrm{atan}\left(\mathrm{1}/\mathrm{3}\right)\:\rightarrow\:\mathrm{n}=\mathrm{3} \\ $$$$\mathrm{A}_{\mathrm{1}} \mathrm{OB}_{\mathrm{1}} =\mathrm{90}\:\rightarrow\:\alpha=\mathrm{atan}\left(\mathrm{3}/\mathrm{2}\right) \\ $$$$\beta=\mathrm{atan}\left(\mathrm{1}/\mathrm{8}\right)\:\rightarrow\:\mathrm{n}=\mathrm{8} \\ $$

Commented by Rasheed.Sindhi last updated on 15/Sep/21

Try to set different values for α & β you′ll get different values of A_1 OB_1 & n (although may be not whole number) You may draw such figure for n=6 in that case α & β will change!

$$\mathcal{T}{ry}\:{to}\:{set}\:{different}\:{values}\:{for}\:\alpha\:\& \\ $$$$\beta\:{you}'{ll}\:{get}\:{different}\:{values}\:{of} \\ $$$$\mathrm{A}_{\mathrm{1}} \mathrm{OB}_{\mathrm{1}} \:\&\:\mathrm{n}\:\left(\mathrm{although}\:\mathrm{may}\:\mathrm{be}\:\mathrm{not}\right. \\ $$$$\left.\mathrm{whole}\:\mathrm{number}\right) \\ $$$${You}\:{may}\:{draw}\:{such}\:{figure}\:{for}\:{n}=\mathrm{6} \\ $$$${in}\:{that}\:{case}\:\alpha\:\&\:\beta\:{will}\:{change}! \\ $$

Commented by Rasheed.Sindhi last updated on 15/Sep/21

Your provided figure is fit for n=4 Now try to measure α & β.For those values of α & β , n will be certainly 4 and A_1 OB_1 will get other value than 90, as you can see from the figure.

$${Your}\:{provided}\:{figure}\:{is}\:{fit}\:{for}\:{n}=\mathrm{4} \\ $$$${Now}\:{try}\:{to}\:{measure}\:\alpha\:\&\:\beta.{For}\:{those} \\ $$$${values}\:{of}\:\alpha\:\&\:\beta\:,\:{n}\:{will}\:{be}\:{certainly} \\ $$$$\mathrm{4}\:{and}\:\:\mathrm{A}_{\mathrm{1}} \mathrm{OB}_{\mathrm{1}} \:{will}\:{get}\:{other}\:{value}\: \\ $$$${than}\:\mathrm{90},\:{as}\:{you}\:{can}\:{see}\:{from}\:{the} \\ $$$${figure}. \\ $$

Commented by mathdanisur last updated on 15/Sep/21

$$\mathrm{Thank}\:\mathrm{you}\:\boldsymbol{\mathrm{S}}\mathrm{er}\:\mathrm{for}\:\mathrm{solution} \\ $$

Commented by Rasheed.Sindhi last updated on 15/Sep/21

$$\mathcal{BTW}\:\:{what}'{s}\:{your}\:{source}\:{of}\:{your} \\ $$$${questions}\:{ser}? \\ $$

Commented by mathdanisur last updated on 15/Sep/21

$$\mathrm{From}\:\mathrm{the}\:\mathrm{school}\:\mathrm{l}\:\mathrm{went}\:\mathrm{to}\:\mathrm{Ser} \\ $$

Commented by mathdanisur last updated on 15/Sep/21

$$\mathrm{and}\:\mathrm{yes}\:\mathrm{Ser}\:\:\mathrm{n}=\mathrm{4}\:\:\mathrm{angle}\:\mathrm{60}° \\ $$

Commented by mathdanisur last updated on 15/Sep/21

$$\mathrm{dear}\:\mathrm{Ser},\:\mathrm{can}\:\mathrm{you}\:\mathrm{contunie}?\:\mathrm{please} \\ $$

Commented by Rasheed.Sindhi last updated on 16/Sep/21

I′ll be happy if I can answer any of your questions.But I′m not an expert. I′m only trying to solve very few questions. Anyway don′t worry there are so many experts in the forum.Of course this forum is a good place to learn... Again request you to share your solutions also. Thanks ser.

$$\mathrm{I}'\mathrm{ll}\:\mathrm{be}\:\mathrm{happy}\:\mathrm{if}\:\mathrm{I}\:\mathrm{can}\:\mathrm{answer}\:\mathrm{any}\:\mathrm{of} \\ $$$$\mathrm{your}\:\mathrm{questions}.\mathrm{But}\:\mathrm{I}'\mathrm{m}\:\mathrm{not}\:\mathrm{an}\:\mathrm{expert}. \\ $$$$\mathrm{I}'\mathrm{m}\:\mathrm{only}\:\boldsymbol{\mathrm{trying}}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{very}\:\mathrm{few}\:\mathrm{questions}. \\ $$$$\mathrm{Anyway}\:\mathrm{don}'\mathrm{t}\:\mathrm{worry}\:\mathrm{there}\:\mathrm{are}\:\mathrm{so} \\ $$$$\mathrm{many}\:\mathrm{experts}\:\mathrm{in}\:\mathrm{the}\:\mathrm{forum}.\mathrm{Of}\:\mathrm{course} \\ $$$$\mathrm{this}\:\mathrm{forum}\:\mathrm{is}\:\mathrm{a}\:\mathrm{good}\:\mathrm{place}\:\mathrm{to}\:\mathrm{learn}… \\ $$$$\mathrm{Again}\:\mathrm{request}\:\mathrm{you}\:\mathrm{to}\:\mathrm{share}\:\mathrm{your} \\ $$$$\mathrm{solutions}\:\mathrm{also}.\:\mathrm{Thanks}\:\mathrm{ser}. \\ $$

Commented by mathdanisur last updated on 16/Sep/21

$$\mathrm{THANK}\:\mathrm{YOU}\:\mathrm{DEAR}\:\boldsymbol{\mathrm{SER}} \\ $$

Answered by Rasheed.Sindhi last updated on 17/Sep/21

An Easy Case:∠A_1 O B_1 =90 △COA_1 ,△DOA_n are right triangles. ∠COA_1 =α+β^(△COA_1 :) , ∠DOA_n =β^(△DOA_n :) tan∠COA_1 =tan(α+β)=(2/1) α+β=tan^(−1) (2) tan∠DOA_n = tanβ=(1/n)⇒β=tan^(−1) ((1/n)) ((tanα )/(tanβ))=((tan( (α+β)−β))/(tanβ)) =((tan(tan^(−1) (2)−tan^(−1) ((1/n))))/(tan(tan^(−1) ((1/n))))) determinant (((tan(a−b)=((tan a−tan b)/(1+tan a.tan b))))) =(((2−(1/n))/(1+2((1/n))))/(1/n))=(((2n−1)/(n+2))/(1/n))=((n(2n−1))/(n+2)) ((tanα )/(tanβ))=((n(2n−1))/(n+2)) ∈Z^+ ⇒n=3,8 ∠A_1 O B_1 =90 { ((n=3)),((n=8)) :}

$$\mathcal{A}{n}\:\mathcal{E}{asy}\:\mathcal{C}{ase}:\angle{A}_{\mathrm{1}} {O}\:{B}_{\mathrm{1}} =\mathrm{90} \\ $$$$\bigtriangleup{COA}_{\mathrm{1}} ,\bigtriangleup{DOA}_{{n}} \:{are}\:{right}\:{triangles}. \\ $$$$\overset{\bigtriangleup{COA}_{\mathrm{1}} :} {\angle{COA}_{\mathrm{1}} =\alpha+\beta}\:,\:\:\:\:\:\overset{\bigtriangleup{DOA}_{{n}} :} {\angle{DOA}_{{n}} =\beta} \\ $$$$\mathrm{tan}\angle{COA}_{\mathrm{1}} =\mathrm{tan}\left(\alpha+\beta\right)=\frac{\mathrm{2}}{\mathrm{1}} \\ $$$$\alpha+\beta=\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{2}\right) \\ $$$$\mathrm{tan}\angle{DOA}_{{n}} =\:\mathrm{tan}\beta=\frac{\mathrm{1}}{{n}}\Rightarrow\beta=\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{{n}}\right)\: \\ $$$$\frac{\mathrm{tan}\alpha\:}{\mathrm{tan}\beta}=\frac{\mathrm{tan}\left(\:\left(\alpha+\beta\right)−\beta\right)}{\mathrm{tan}\beta} \\ $$$$=\frac{\mathrm{tan}\left(\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{2}\right)−\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{{n}}\right)\right)}{\mathrm{tan}\left(\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{{n}}\right)\right)} \\ $$$$\begin{array}{|c|}{\mathrm{tan}\left({a}−{b}\right)=\frac{\mathrm{tan}\:{a}−\mathrm{tan}\:{b}}{\mathrm{1}+\mathrm{tan}\:{a}.\mathrm{tan}\:{b}}}\\\hline\end{array} \\ $$$$=\frac{\frac{\mathrm{2}−\frac{\mathrm{1}}{{n}}}{\mathrm{1}+\mathrm{2}\left(\frac{\mathrm{1}}{{n}}\right)}}{\frac{\mathrm{1}}{{n}}}=\frac{\frac{\mathrm{2}{n}−\mathrm{1}}{{n}+\mathrm{2}}}{\mathrm{1}/{n}}=\frac{{n}\left(\mathrm{2}{n}−\mathrm{1}\right)}{{n}+\mathrm{2}} \\ $$$$\frac{\mathrm{tan}\alpha\:}{\mathrm{tan}\beta}=\frac{{n}\left(\mathrm{2}{n}−\mathrm{1}\right)}{{n}+\mathrm{2}}\:\in\mathbb{Z}^{+} \Rightarrow{n}=\mathrm{3},\mathrm{8} \\ $$$$\angle{A}_{\mathrm{1}} {O}\:{B}_{\mathrm{1}} =\mathrm{90}\:\begin{cases}{{n}=\mathrm{3}}\\{{n}=\mathrm{8}}\end{cases} \\ $$

Commented by Rasheed.Sindhi last updated on 17/Sep/21