Question Number 154258 by liberty last updated on 16/Sep/21

Answered by som(math1967) last updated on 16/Sep/21
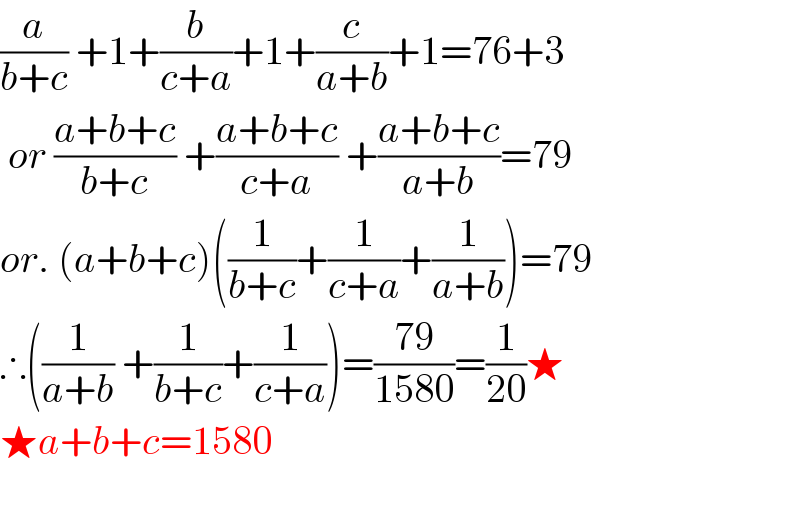
$$\frac{{a}}{{b}+{c}}\:+\mathrm{1}+\frac{{b}}{{c}+{a}}+\mathrm{1}+\frac{{c}}{{a}+{b}}+\mathrm{1}=\mathrm{76}+\mathrm{3} \\ $$$$\:{or}\:\frac{{a}+{b}+{c}}{{b}+{c}}\:+\frac{{a}+{b}+{c}}{{c}+{a}}\:+\frac{{a}+{b}+{c}}{{a}+{b}}=\mathrm{79} \\ $$$${or}.\:\left({a}+{b}+{c}\right)\left(\frac{\mathrm{1}}{{b}+{c}}+\frac{\mathrm{1}}{{c}+{a}}+\frac{\mathrm{1}}{{a}+{b}}\right)=\mathrm{79} \\ $$$$\therefore\left(\frac{\mathrm{1}}{{a}+{b}}\:+\frac{\mathrm{1}}{{b}+{c}}+\frac{\mathrm{1}}{{c}+{a}}\right)=\frac{\mathrm{79}}{\mathrm{1580}}=\frac{\mathrm{1}}{\mathrm{20}}\bigstar \\ $$$$\bigstar{a}+{b}+{c}=\mathrm{1580} \\ $$$$ \\ $$
Commented by liberty last updated on 16/Sep/21

$${yes} \\ $$
