Question Number 154292 by mnjuly1970 last updated on 16/Sep/21
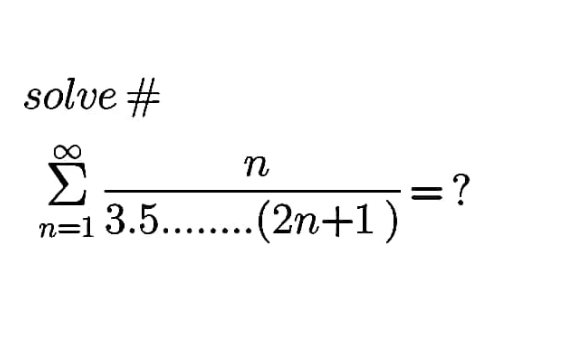
Answered by ARUNG_Brandon_MBU last updated on 16/Sep/21
![S=Σ_(n=1) ^∞ (n/(3∙5∙∙∙(2n+1)))=Σ_(n=1) ^∞ ((n(2∙4∙6∙∙∙2n))/(2∙3∙4∙5∙6∙∙∙(2n)(2n+1))) =Σ_(n=1) ^∞ ((2^n n(n!))/((2n+1)!))=Σ_(n=1) ^∞ (2^n /((n−1)!))∙(((n!)(n!))/((2n+1)!)) =Σ_(n=1) ^∞ (2^n /((n−1)!))β(n+1, n+1)=Σ_(n=1) ^∞ (2^n /((n−1)!))∫_0 ^1 x^n (1−x)^n dx =∫_0 ^1 Σ_(n=1) ^∞ (((2x−2x^2 )^n )/((n−1)!))dx=∫_0 ^1 (2x−2x^2 )Σ_(n=0) ^∞ (((2x−2x^2 )^n )/(n!))dx =∫_0 ^1 (2x−2x^2 )e^(2x−2x^2 ) dx=∫_0 ^1 x(2−2x)e^(2x−2x^2 ) dx =∫_0 ^1 x[(1/2)(2−4x)+1]e^(2x−2x^2 ) dx=(1/2)∫_0 ^1 x∙(2−4x)e^(2x−2x^2 ) dx+∫_0 ^1 xe^(2x−2x^2 ) dx =(1/2)∫_0 ^1 x∙(2−4x)e^(2x−2x^2 ) dx−(1/4)∫_0 ^1 (2−4x)e^(2x−2x^2 ) dx+(1/2)∫_0 ^1 e^(2x−2x^2 ) dx =(1/2)[xe^(2x−2x^2 ) −∫e^(2x−2x^2 ) dx]_0 ^1 −(1/4)∫_0 ^1 e^(2x−2x^2 ) dx+(1/2)∫_0 ^1 e^(2x−2x^2 ) dx =(1/2)−(1/4)∫_0 ^1 e^(−(2x^2 −2x)) dx=(1/2)−(1/4)∫_0 ^1 e^(−(((√2)x−(1/( (√2))))^2 −(1/2))) dx =(1/2)−((√e)/4)∫_0 ^1 e^(−((√2)x−(1/( (√2))))^2 ) dx, u=(√2)x−(1/( (√2)))⇒du=(√2)dx =(1/2)−((√e)/(4(√2)))∫_(−(1/( (√2)))) ^(1/( (√2))) e^(−u^2 ) du=(1/2)−(√((πe)/(32)))erf((1/( (√2))))](https://www.tinkutara.com/question/Q154297.png)
$${S}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{n}}{\mathrm{3}\centerdot\mathrm{5}\centerdot\centerdot\centerdot\left(\mathrm{2}{n}+\mathrm{1}\right)}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{n}\left(\mathrm{2}\centerdot\mathrm{4}\centerdot\mathrm{6}\centerdot\centerdot\centerdot\mathrm{2}{n}\right)}{\mathrm{2}\centerdot\mathrm{3}\centerdot\mathrm{4}\centerdot\mathrm{5}\centerdot\mathrm{6}\centerdot\centerdot\centerdot\left(\mathrm{2}{n}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)} \\ $$$$\:\:\:=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{2}^{{n}} {n}\left({n}!\right)}{\left(\mathrm{2}{n}+\mathrm{1}\right)!}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{2}^{{n}} }{\left({n}−\mathrm{1}\right)!}\centerdot\frac{\left({n}!\right)\left({n}!\right)}{\left(\mathrm{2}{n}+\mathrm{1}\right)!} \\ $$$$\:\:\:=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{2}^{{n}} }{\left({n}−\mathrm{1}\right)!}\beta\left({n}+\mathrm{1},\:{n}+\mathrm{1}\right)=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{2}^{{n}} }{\left({n}−\mathrm{1}\right)!}\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{n}} \left(\mathrm{1}−{x}\right)^{{n}} {dx} \\ $$$$\:\:\:=\int_{\mathrm{0}} ^{\mathrm{1}} \underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(\mathrm{2}{x}−\mathrm{2}{x}^{\mathrm{2}} \right)^{{n}} }{\left({n}−\mathrm{1}\right)!}{dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{2}{x}−\mathrm{2}{x}^{\mathrm{2}} \right)\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(\mathrm{2}{x}−\mathrm{2}{x}^{\mathrm{2}} \right)^{{n}} }{{n}!}{dx} \\ $$$$\:\:\:=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{2}{x}−\mathrm{2}{x}^{\mathrm{2}} \right){e}^{\mathrm{2}{x}−\mathrm{2}{x}^{\mathrm{2}} } {dx}=\int_{\mathrm{0}} ^{\mathrm{1}} {x}\left(\mathrm{2}−\mathrm{2}{x}\right){e}^{\mathrm{2}{x}−\mathrm{2}{x}^{\mathrm{2}} } {dx} \\ $$$$\:\:\:=\int_{\mathrm{0}} ^{\mathrm{1}} {x}\left[\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}−\mathrm{4}{x}\right)+\mathrm{1}\right]{e}^{\mathrm{2}{x}−\mathrm{2}{x}^{\mathrm{2}} } {dx}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} {x}\centerdot\left(\mathrm{2}−\mathrm{4}{x}\right){e}^{\mathrm{2}{x}−\mathrm{2}{x}^{\mathrm{2}} } {dx}+\int_{\mathrm{0}} ^{\mathrm{1}} {xe}^{\mathrm{2}{x}−\mathrm{2}{x}^{\mathrm{2}} } {dx} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} {x}\centerdot\left(\mathrm{2}−\mathrm{4}{x}\right){e}^{\mathrm{2}{x}−\mathrm{2}{x}^{\mathrm{2}} } {dx}−\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{2}−\mathrm{4}{x}\right){e}^{\mathrm{2}{x}−\mathrm{2}{x}^{\mathrm{2}} } {dx}+\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} {e}^{\mathrm{2}{x}−\mathrm{2}{x}^{\mathrm{2}} } {dx} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\left[{xe}^{\mathrm{2}{x}−\mathrm{2}{x}^{\mathrm{2}} } −\int{e}^{\mathrm{2}{x}−\mathrm{2}{x}^{\mathrm{2}} } {dx}\right]_{\mathrm{0}} ^{\mathrm{1}} −\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\mathrm{1}} {e}^{\mathrm{2}{x}−\mathrm{2}{x}^{\mathrm{2}} } {dx}+\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} {e}^{\mathrm{2}{x}−\mathrm{2}{x}^{\mathrm{2}} } {dx} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\mathrm{1}} {e}^{−\left(\mathrm{2}{x}^{\mathrm{2}} −\mathrm{2}{x}\right)} {dx}=\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\mathrm{1}} {e}^{−\left(\left(\sqrt{\mathrm{2}}{x}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}}\right)} {dx} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{{e}}}{\mathrm{4}}\int_{\mathrm{0}} ^{\mathrm{1}} {e}^{−\left(\sqrt{\mathrm{2}}{x}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} } {dx},\:{u}=\sqrt{\mathrm{2}}{x}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\Rightarrow{du}=\sqrt{\mathrm{2}}{dx} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{{e}}}{\mathrm{4}\sqrt{\mathrm{2}}}\int_{−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} ^{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} {e}^{−{u}^{\mathrm{2}} } {du}=\frac{\mathrm{1}}{\mathrm{2}}−\sqrt{\frac{\pi{e}}{\mathrm{32}}}{erf}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right) \\ $$
Answered by ARUNG_Brandon_MBU last updated on 16/Sep/21
![S=Σ_(n=1) ^∞ ((n!)/(3.5...(2n+1)))=Σ_(n=1) ^∞ ((2^n (n!)(n!))/((2n+1)!)) =Σ_(n=1) ^∞ 2^n β(n+1, n+1)=Σ_(n=1) ^∞ 2^n ∫_0 ^1 x^n (1−x)^n dx =∫_0 ^1 Σ_(n=1) ^∞ (2x−2x^2 )^n dx=∫_0 ^1 ((2x−2x^2 )/(2x^2 −2x+1))dx =∫_0 ^1 ((1/(2x^2 −2x+1))−1)dx=(1/2)∫_0 ^1 (dx/((x−(1/2))^2 +(1/4)))−1 =(1/2)∙(2/1)[arctan(2x−1)]_0 ^1 −1=(π/4)+(π/4)−1=(π/2)−1](https://www.tinkutara.com/question/Q154298.png)
$${S}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{n}!}{\mathrm{3}.\mathrm{5}…\left(\mathrm{2}{n}+\mathrm{1}\right)}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{2}^{{n}} \left({n}!\right)\left({n}!\right)}{\left(\mathrm{2}{n}+\mathrm{1}\right)!} \\ $$$$\:\:\:=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\mathrm{2}^{{n}} \beta\left({n}+\mathrm{1},\:{n}+\mathrm{1}\right)=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\mathrm{2}^{{n}} \int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{n}} \left(\mathrm{1}−{x}\right)^{{n}} {dx} \\ $$$$\:\:\:=\int_{\mathrm{0}} ^{\mathrm{1}} \underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\mathrm{2}{x}−\mathrm{2}{x}^{\mathrm{2}} \right)^{{n}} {dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{2}{x}−\mathrm{2}{x}^{\mathrm{2}} }{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}}{dx} \\ $$$$\:\:\:=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}}−\mathrm{1}\right){dx}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dx}}{\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{4}}}−\mathrm{1} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\centerdot\frac{\mathrm{2}}{\mathrm{1}}\left[\mathrm{arctan}\left(\mathrm{2}{x}−\mathrm{1}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} −\mathrm{1}=\frac{\pi}{\mathrm{4}}+\frac{\pi}{\mathrm{4}}−\mathrm{1}=\frac{\pi}{\mathrm{2}}−\mathrm{1} \\ $$
