Menu Close

Question-154415

Tinku Tara 0 Comments
Pin




Question Number 154415 by mr W last updated on 18/Sep/21
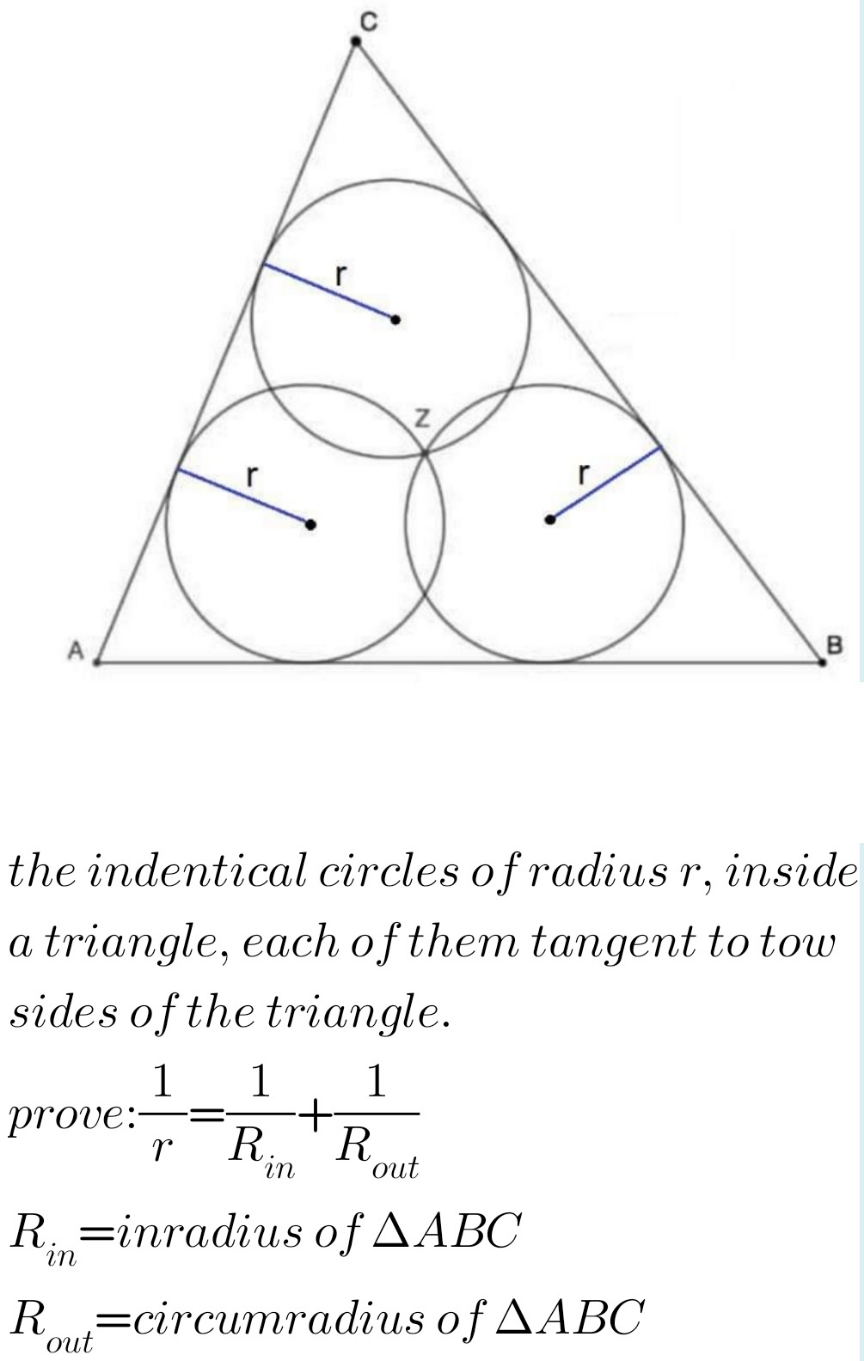
Commented by mr W last updated on 18/Sep/21
[Q154210]
$$\left[{Q}\mathrm{154210}\right] \\ $$
Answered by mr W last updated on 18/Sep/21
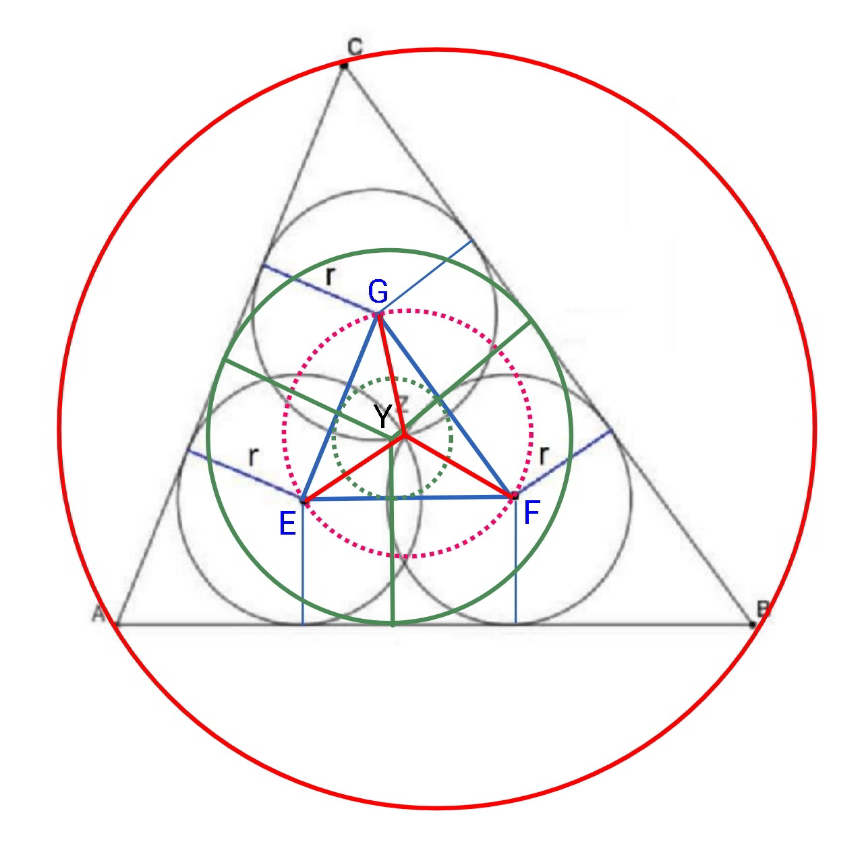
Commented by mr W last updated on 18/Sep/21
say E,F,G are the centers of identical circles with radius r. Z is the circumcenter of ΔEFG, since ZE=ZF=ZG=r, and the circum− radius of ΔEFG is r_(out) =r. say the center of incircle of ΔEFG is Y and the inradius of ΔEFG is r_(in) . the distances from Y to the sides of ΔEFG are r_(in) . the distances from Y to the sides of ΔABC are r_(in) +r. that means Y is also the incenter of ΔABC, and R_(in) =r_(in) +r. it is obviour that ΔABC∼ΔEFG, therefore ((circumradius of ΔEFG)/(circumradius of ΔABC))=((inradius of ΔEFG)/(inradius of ΔABC)) ⇒(r_(out) /R_(out) )=(r_(in) /R_(in) ) ⇒(r/R_(out) )=(r_(in) /(r_(in) +r)) ⇒(1/R_(out) )=(r_(in) /((r_(in) +r)r)) (1/R_(in) )+(1/R_(out) )=(1/(r_(in) +r))+(r_(in) /((r_(in) +r)r))=(1/r) ⇒(1/r)=(1/R_(in) )+(1/R_(out) )
$${say}\:{E},{F},{G}\:{are}\:{the}\:{centers}\:{of}\:{identical} \\ $$$${circles}\:{with}\:{radius}\:{r}. \\ $$$${Z}\:{is}\:{the}\:{circumcenter}\:{of}\:\Delta{EFG},\:{since} \\ $$$${ZE}={ZF}={ZG}={r},\:{and}\:{the}\:{circum}− \\ $$$${radius}\:{of}\:\Delta{EFG}\:{is}\:{r}_{{out}} ={r}. \\ $$$${say}\:{the}\:{center}\:{of}\:{incircle}\:{of}\:\Delta{EFG} \\ $$$${is}\:{Y}\:{and}\:{the}\:{inradius}\:{of}\:\Delta{EFG}\:{is}\:{r}_{{in}} . \\ $$$${the}\:{distances}\:{from}\:{Y}\:{to}\:{the}\:{sides}\:{of} \\ $$$$\Delta{EFG}\:{are}\:{r}_{{in}} . \\ $$$${the}\:{distances}\:{from}\:{Y}\:{to}\:{the}\:{sides}\:{of} \\ $$$$\Delta{ABC}\:{are}\:{r}_{{in}} +{r}.\:{that}\:{means}\:{Y}\:{is} \\ $$$${also}\:{the}\:{incenter}\:{of}\:\Delta{ABC},\:{and} \\ $$$${R}_{{in}} ={r}_{{in}} +{r}. \\ $$$${it}\:{is}\:{obviour}\:{that}\:\Delta{ABC}\sim\Delta{EFG}, \\ $$$${therefore}\: \\ $$$$\frac{{circumradius}\:{of}\:\Delta{EFG}}{{circumradius}\:{of}\:\Delta{ABC}}=\frac{{inradius}\:{of}\:\Delta{EFG}}{{inradius}\:{of}\:\Delta{ABC}} \\ $$$$\Rightarrow\frac{{r}_{{out}} }{{R}_{{out}} }=\frac{{r}_{{in}} }{{R}_{{in}} } \\ $$$$\Rightarrow\frac{{r}}{{R}_{{out}} }=\frac{{r}_{{in}} }{{r}_{{in}} +{r}} \\ $$$$\Rightarrow\frac{\mathrm{1}}{{R}_{{out}} }=\frac{{r}_{{in}} }{\left({r}_{{in}} +{r}\right){r}} \\ $$$$\frac{\mathrm{1}}{{R}_{{in}} }+\frac{\mathrm{1}}{{R}_{{out}} }=\frac{\mathrm{1}}{{r}_{{in}} +{r}}+\frac{{r}_{{in}} }{\left({r}_{{in}} +{r}\right){r}}=\frac{\mathrm{1}}{{r}} \\ $$$$\Rightarrow\frac{\mathrm{1}}{{r}}=\frac{\mathrm{1}}{{R}_{{in}} }+\frac{\mathrm{1}}{{R}_{{out}} } \\ $$
Commented by Tawa11 last updated on 18/Sep/21
Weldone sir
$$\mathrm{Weldone}\:\mathrm{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *