Question-154429

Question Number 154429 by liberty last updated on 18/Sep/21

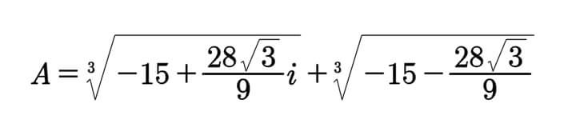
Commented by liberty last updated on 18/Sep/21

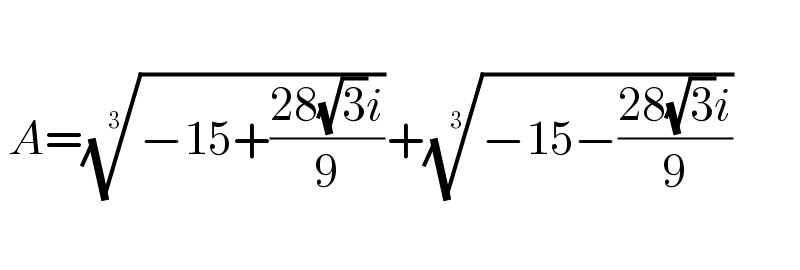
A=((−15+((28(√3)i)/9)))^(1/3) +((−15−((28(√3)i)/9)))^(1/3)

$$ \\ $$$$\:{A}=\sqrt[{\mathrm{3}}]{−\mathrm{15}+\frac{\mathrm{28}\sqrt{\mathrm{3}}{i}}{\mathrm{9}}}+\sqrt[{\mathrm{3}}]{−\mathrm{15}−\frac{\mathrm{28}\sqrt{\mathrm{3}}{i}}{\mathrm{9}}} \\ $$$$ \\ $$

Commented by EDWIN88 last updated on 18/Sep/21

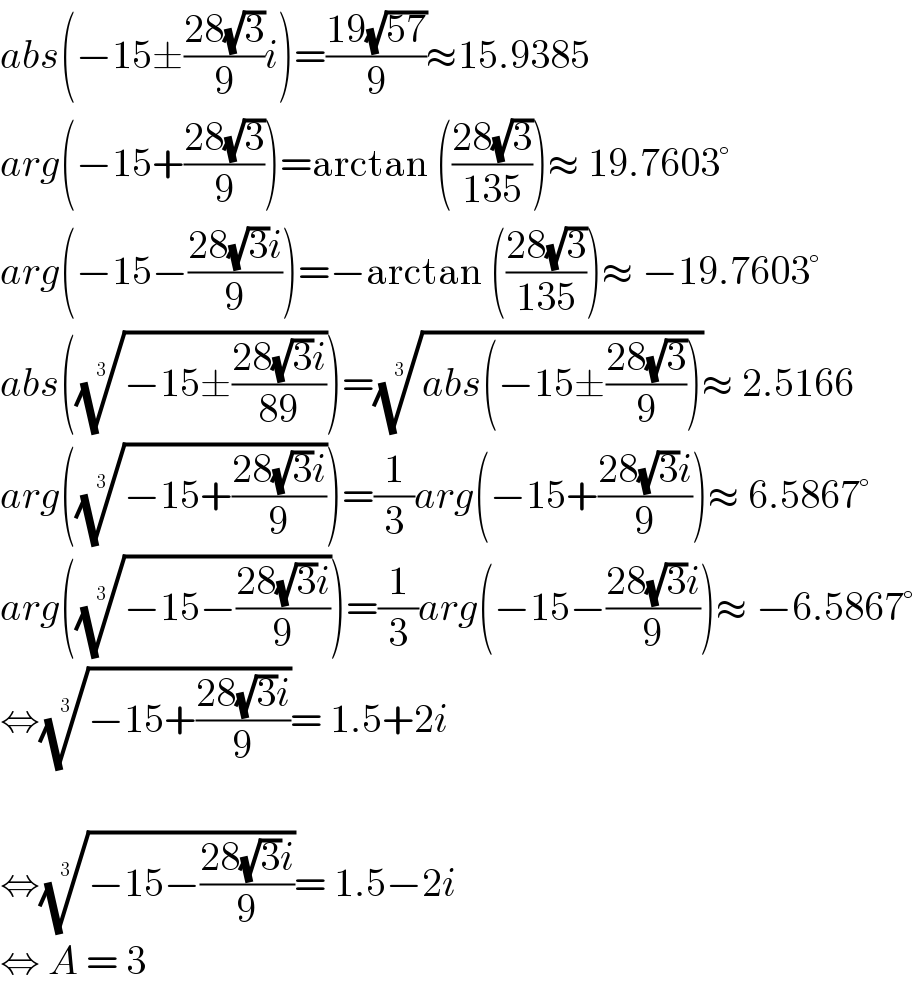
abs(−15±((28(√3))/9)i)=((19(√(57)))/9)≈15.9385 arg(−15+((28(√3))/9))=arctan (((28(√3))/(135)))≈ 19.7603° arg(−15−((28(√3)i)/9))=−arctan (((28(√3))/(135)))≈ −19.7603° abs(((−15±((28(√3)i)/(89))))^(1/3) )=((abs(−15±((28(√3))/9))))^(1/3) ≈ 2.5166 arg(((−15+((28(√3)i)/9)))^(1/3) )=(1/3)arg(−15+((28(√3)i)/9))≈ 6.5867° arg(((−15−((28(√3)i)/9)))^(1/3) )=(1/3)arg(−15−((28(√3)i)/9))≈ −6.5867° ⇔((−15+((28(√3)i)/9)))^(1/3) = 1.5+2i ⇔((−15−((28(√3)i)/9)))^(1/3) = 1.5−2i ⇔ A = 3

$${abs}\left(−\mathrm{15}\pm\frac{\mathrm{28}\sqrt{\mathrm{3}}}{\mathrm{9}}{i}\right)=\frac{\mathrm{19}\sqrt{\mathrm{57}}}{\mathrm{9}}\approx\mathrm{15}.\mathrm{9385} \\ $$$${arg}\left(−\mathrm{15}+\frac{\mathrm{28}\sqrt{\mathrm{3}}}{\mathrm{9}}\right)=\mathrm{arctan}\:\left(\frac{\mathrm{28}\sqrt{\mathrm{3}}}{\mathrm{135}}\right)\approx\:\mathrm{19}.\mathrm{7603}° \\ $$$${arg}\left(−\mathrm{15}−\frac{\mathrm{28}\sqrt{\mathrm{3}}{i}}{\mathrm{9}}\right)=−\mathrm{arctan}\:\left(\frac{\mathrm{28}\sqrt{\mathrm{3}}}{\mathrm{135}}\right)\approx\:−\mathrm{19}.\mathrm{7603}° \\ $$$${abs}\left(\sqrt[{\mathrm{3}}]{−\mathrm{15}\pm\frac{\mathrm{28}\sqrt{\mathrm{3}}{i}}{\mathrm{89}}}\right)=\sqrt[{\mathrm{3}}]{{abs}\left(−\mathrm{15}\pm\frac{\mathrm{28}\sqrt{\mathrm{3}}}{\mathrm{9}}\right)}\approx\:\mathrm{2}.\mathrm{5166} \\ $$$${arg}\left(\sqrt[{\mathrm{3}}]{−\mathrm{15}+\frac{\mathrm{28}\sqrt{\mathrm{3}}{i}}{\mathrm{9}}}\right)=\frac{\mathrm{1}}{\mathrm{3}}{arg}\left(−\mathrm{15}+\frac{\mathrm{28}\sqrt{\mathrm{3}}{i}}{\mathrm{9}}\right)\approx\:\mathrm{6}.\mathrm{5867}° \\ $$$${arg}\left(\sqrt[{\mathrm{3}}]{−\mathrm{15}−\frac{\mathrm{28}\sqrt{\mathrm{3}}{i}}{\mathrm{9}}}\right)=\frac{\mathrm{1}}{\mathrm{3}}{arg}\left(−\mathrm{15}−\frac{\mathrm{28}\sqrt{\mathrm{3}}{i}}{\mathrm{9}}\right)\approx\:−\mathrm{6}.\mathrm{5867}° \\ $$$$\Leftrightarrow\sqrt[{\mathrm{3}}]{−\mathrm{15}+\frac{\mathrm{28}\sqrt{\mathrm{3}}{i}}{\mathrm{9}}}=\:\mathrm{1}.\mathrm{5}+\mathrm{2}{i} \\ $$$$\:\:\:\:\:\: \\ $$$$\Leftrightarrow\sqrt[{\mathrm{3}}]{−\mathrm{15}−\frac{\mathrm{28}\sqrt{\mathrm{3}}{i}}{\mathrm{9}}}=\:\mathrm{1}.\mathrm{5}−\mathrm{2}{i} \\ $$$$\Leftrightarrow\:{A}\:=\:\mathrm{3}\: \\ $$

Commented by liberty last updated on 18/Sep/21

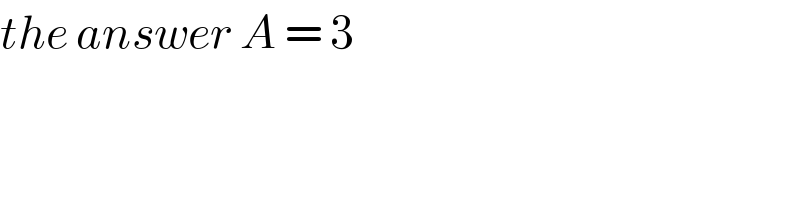
$${the}\:{answer}\:{A}\:=\:\mathrm{3} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply