Question Number 154444 by Rasheed.Sindhi last updated on 18/Sep/21

Commented by Rasheed.Sindhi last updated on 18/Sep/21

$$\mathrm{Question}#\mathrm{154100}\:\:\mathrm{Reposted} \\ $$
Answered by Rasheed.Sindhi last updated on 18/Sep/21

$$\:\:\sqrt{\mathrm{5}{x}+\mathrm{1}}+\sqrt{{x}−\mathrm{2}}=\sqrt{\mathrm{8}{x}+\mathrm{1}}\:\:\:;\:\mathbb{S}\mathrm{olve}. \\ $$$$\underset{{a}} {\underbrace{\sqrt{\frac{\mathrm{8}{x}+\mathrm{1}}{{x}−\mathrm{2}}}\:}}−\underset{{b}} {\underbrace{\sqrt{\frac{\mathrm{5}{x}+\mathrm{1}}{{x}−\mathrm{2}}}\:}}=\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:{a}−{b}=\mathrm{1}……….{A} \\ $$$$\:\:{a}^{\mathrm{2}} −{b}^{\mathrm{2}} =\left(\sqrt{\frac{\mathrm{8}{x}+\mathrm{1}}{{x}−\mathrm{2}}}\:\right)^{\mathrm{2}} −\left(\sqrt{\frac{\mathrm{5}{x}+\mathrm{1}}{{x}−\mathrm{2}}}\:\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:{a}^{\mathrm{2}} −{b}^{\mathrm{2}} =\frac{\mathrm{3}{x}}{{x}−\mathrm{2}}………{B} \\ $$$${B}/{A}:\:\:{a}+{b}=\frac{\mathrm{3}{x}}{{x}−\mathrm{2}}……{C} \\ $$$${A}+{C}:\:\mathrm{2}{a}=\frac{\mathrm{3}{x}}{{x}−\mathrm{2}}+\mathrm{1}=\frac{\mathrm{4}{x}−\mathrm{2}}{{x}−\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:{a}=\frac{\mathrm{2}{x}−\mathrm{1}}{{x}−\mathrm{2}} \\ $$$$\:\:\:\:\:\frac{\mathrm{8}{x}+\mathrm{1}}{{x}−\mathrm{2}}=\left(\frac{\mathrm{2}{x}−\mathrm{1}}{{x}−\mathrm{2}}\right)^{\mathrm{2}} \\ $$$$\:\:\:\mathrm{8}{x}+\mathrm{1}=\frac{\mathrm{4}{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{1}}{{x}−\mathrm{2}} \\ $$$$\:\:\:\mathrm{8}{x}^{\mathrm{2}} +{x}−\mathrm{16}{x}−\mathrm{2}=\mathrm{4}{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{1} \\ $$$$\:\:\:\:\mathrm{4}{x}^{\mathrm{2}} −\mathrm{11}{x}−\mathrm{3}=\mathrm{0} \\ $$$$\:\:\:\:\:\mathrm{4}{x}^{\mathrm{2}} −\mathrm{12}{x}+{x}−\mathrm{3}=\mathrm{0} \\ $$$$\:\:\:\:\:\mathrm{4}{x}\left({x}−\mathrm{3}\right)+\mathrm{1}\left({x}−\mathrm{3}\right)=\mathrm{0} \\ $$$$\:\:\:\:\left({x}−\mathrm{3}\right)\left(\mathrm{4}{x}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\:\:\:\:{x}=\mathrm{3}\:\left(\checkmark\right)\:\:\mid\:\:{x}=−\frac{\mathrm{1}}{\mathrm{4}}\left({false}\right) \\ $$
Answered by cherokeesay last updated on 18/Sep/21
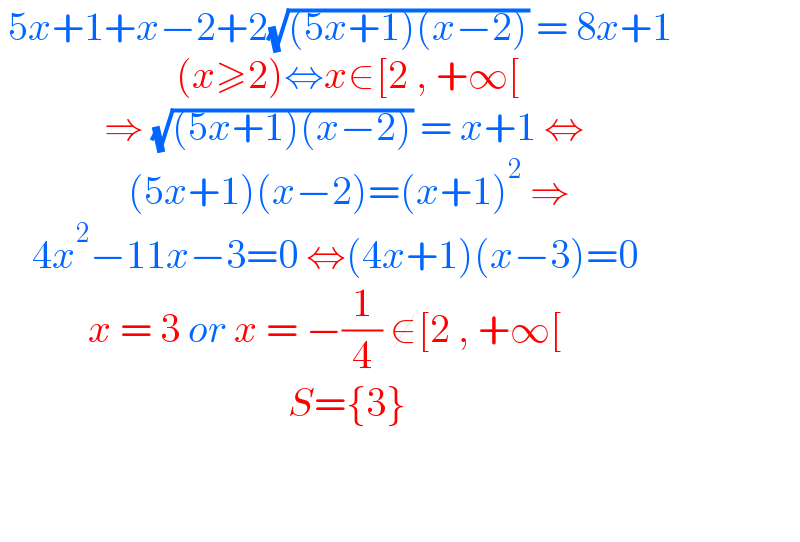
$$\:\mathrm{5}{x}+\mathrm{1}+{x}−\mathrm{2}+\mathrm{2}\sqrt{\left(\mathrm{5}{x}+\mathrm{1}\right)\left({x}−\mathrm{2}\right)}\:=\:\mathrm{8}{x}+\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left({x}\geqslant\mathrm{2}\right)\Leftrightarrow{x}\in\left[\mathrm{2}\:,\:+\infty\left[\right.\right. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:\sqrt{\left(\mathrm{5}{x}+\mathrm{1}\right)\left({x}−\mathrm{2}\right)}\:=\:{x}+\mathrm{1}\:\Leftrightarrow \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{5}{x}+\mathrm{1}\right)\left({x}−\mathrm{2}\right)=\left({x}+\mathrm{1}\right)^{\mathrm{2}} \:\Rightarrow \\ $$$$\:\:\:\:\mathrm{4}{x}^{\mathrm{2}} −\mathrm{11}{x}−\mathrm{3}=\mathrm{0}\:\Leftrightarrow\left(\mathrm{4}{x}+\mathrm{1}\right)\left({x}−\mathrm{3}\right)=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:{x}\:=\:\mathrm{3}\:{or}\:{x}\:=\:−\frac{\mathrm{1}}{\mathrm{4}}\:\notin\left[\mathrm{2}\:,\:+\infty\left[\right.\right. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{S}=\left\{\mathrm{3}\right\} \\ $$$$ \\ $$$$ \\ $$
Commented by Rasheed.Sindhi last updated on 19/Sep/21

$$\mathbb{T}\mathrm{han}\Bbbk\mathrm{s}\:\mathrm{ser}! \\ $$
