Question Number 154542 by SANOGO last updated on 19/Sep/21

Answered by qaz last updated on 19/Sep/21
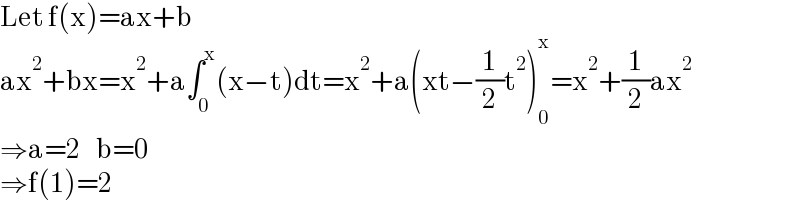
$$\mathrm{Let}\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{ax}+\mathrm{b} \\ $$$$\mathrm{ax}^{\mathrm{2}} +\mathrm{bx}=\mathrm{x}^{\mathrm{2}} +\mathrm{a}\int_{\mathrm{0}} ^{\mathrm{x}} \left(\mathrm{x}−\mathrm{t}\right)\mathrm{dt}=\mathrm{x}^{\mathrm{2}} +\mathrm{a}\left(\mathrm{xt}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{t}^{\mathrm{2}} \right)_{\mathrm{0}} ^{\mathrm{x}} =\mathrm{x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ax}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{a}=\mathrm{2}\:\:\:\:\mathrm{b}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{1}\right)=\mathrm{2} \\ $$
Commented by SANOGO last updated on 19/Sep/21
$${merci}\:{bien} \\ $$
