Menu Close

Question-15471

Tinku Tara 0 Comments
Pin




Question Number 15471 by Mr easymsn last updated on 10/Jun/17
Answered by sma3l2996 last updated on 10/Jun/17
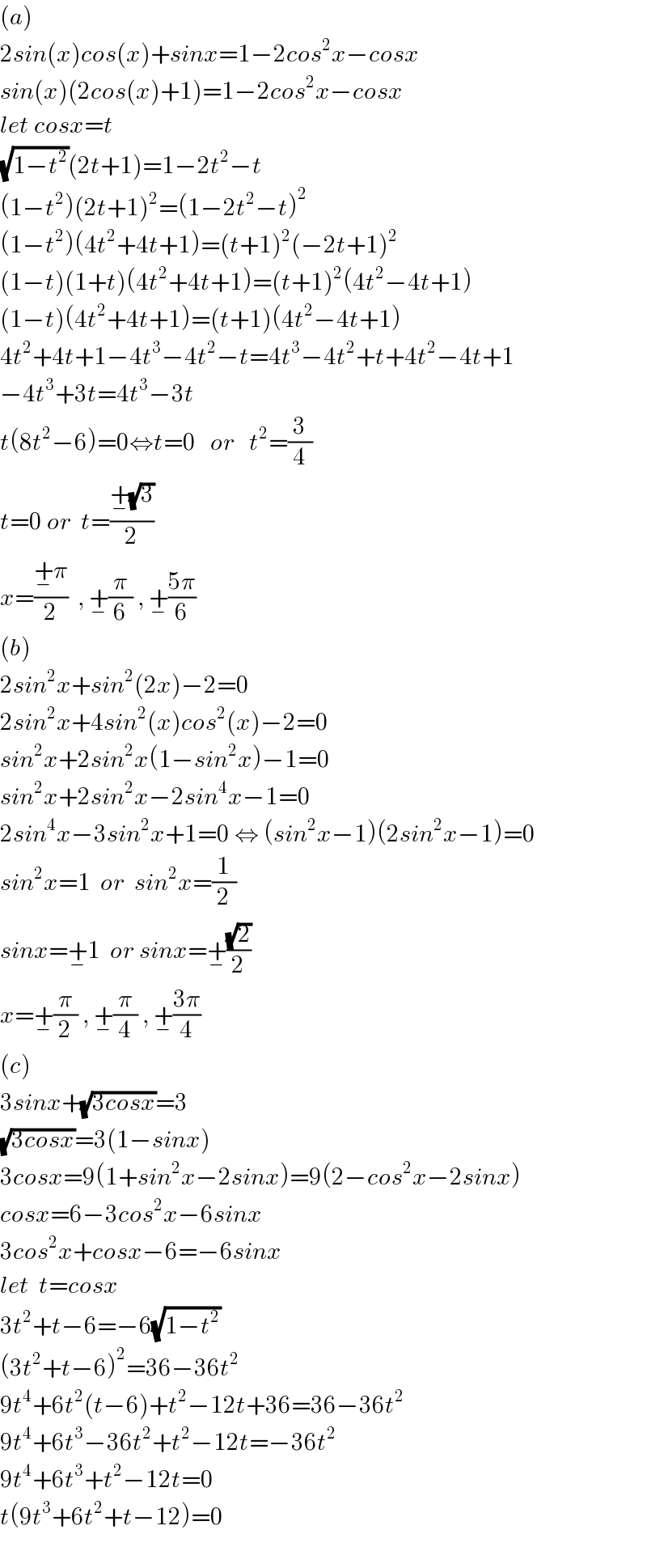
(a) 2sin(x)cos(x)+sinx=1−2cos^2 x−cosx sin(x)(2cos(x)+1)=1−2cos^2 x−cosx let cosx=t (√(1−t^2 ))(2t+1)=1−2t^2 −t (1−t^2 )(2t+1)^2 =(1−2t^2 −t)^2 (1−t^2 )(4t^2 +4t+1)=(t+1)^2 (−2t+1)^2 (1−t)(1+t)(4t^2 +4t+1)=(t+1)^2 (4t^2 −4t+1) (1−t)(4t^2 +4t+1)=(t+1)(4t^2 −4t+1) 4t^2 +4t+1−4t^3 −4t^2 −t=4t^3 −4t^2 +t+4t^2 −4t+1 −4t^3 +3t=4t^3 −3t t(8t^2 −6)=0⇔t=0 or t^2 =(3/4) t=0 or t=((+_− (√3))/2) x=((+_− π)/2) , +_− (π/6) , +_− ((5π)/6) (b) 2sin^2 x+sin^2 (2x)−2=0 2sin^2 x+4sin^2 (x)cos^2 (x)−2=0 sin^2 x+2sin^2 x(1−sin^2 x)−1=0 sin^2 x+2sin^2 x−2sin^4 x−1=0 2sin^4 x−3sin^2 x+1=0 ⇔ (sin^2 x−1)(2sin^2 x−1)=0 sin^2 x=1 or sin^2 x=(1/2) sinx=+_− 1 or sinx=+_− ((√2)/2) x=+_− (π/2) , +_− (π/4) , +_− ((3π)/4) (c) 3sinx+(√(3cosx))=3 (√(3cosx))=3(1−sinx) 3cosx=9(1+sin^2 x−2sinx)=9(2−cos^2 x−2sinx) cosx=6−3cos^2 x−6sinx 3cos^2 x+cosx−6=−6sinx let t=cosx 3t^2 +t−6=−6(√(1−t^2 )) (3t^2 +t−6)^2 =36−36t^2 9t^4 +6t^2 (t−6)+t^2 −12t+36=36−36t^2 9t^4 +6t^3 −36t^2 +t^2 −12t=−36t^2 9t^4 +6t^3 +t^2 −12t=0 t(9t^3 +6t^2 +t−12)=0
$$\left({a}\right) \\ $$$$\mathrm{2}{sin}\left({x}\right){cos}\left({x}\right)+{sinx}=\mathrm{1}−\mathrm{2}{cos}^{\mathrm{2}} {x}−{cosx} \\ $$$${sin}\left({x}\right)\left(\mathrm{2}{cos}\left({x}\right)+\mathrm{1}\right)=\mathrm{1}−\mathrm{2}{cos}^{\mathrm{2}} {x}−{cosx} \\ $$$${let}\:{cosx}={t} \\ $$$$\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }\left(\mathrm{2}{t}+\mathrm{1}\right)=\mathrm{1}−\mathrm{2}{t}^{\mathrm{2}} −{t} \\ $$$$\left(\mathrm{1}−{t}^{\mathrm{2}} \right)\left(\mathrm{2}{t}+\mathrm{1}\right)^{\mathrm{2}} =\left(\mathrm{1}−\mathrm{2}{t}^{\mathrm{2}} −{t}\right)^{\mathrm{2}} \\ $$$$\left(\mathrm{1}−{t}^{\mathrm{2}} \right)\left(\mathrm{4}{t}^{\mathrm{2}} +\mathrm{4}{t}+\mathrm{1}\right)=\left({t}+\mathrm{1}\right)^{\mathrm{2}} \left(−\mathrm{2}{t}+\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\left(\mathrm{1}−{t}\right)\left(\mathrm{1}+{t}\right)\left(\mathrm{4}{t}^{\mathrm{2}} +\mathrm{4}{t}+\mathrm{1}\right)=\left({t}+\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{4}{t}^{\mathrm{2}} −\mathrm{4}{t}+\mathrm{1}\right) \\ $$$$\left(\mathrm{1}−{t}\right)\left(\mathrm{4}{t}^{\mathrm{2}} +\mathrm{4}{t}+\mathrm{1}\right)=\left({t}+\mathrm{1}\right)\left(\mathrm{4}{t}^{\mathrm{2}} −\mathrm{4}{t}+\mathrm{1}\right) \\ $$$$\mathrm{4}{t}^{\mathrm{2}} +\mathrm{4}{t}+\mathrm{1}−\mathrm{4}{t}^{\mathrm{3}} −\mathrm{4}{t}^{\mathrm{2}} −{t}=\mathrm{4}{t}^{\mathrm{3}} −\mathrm{4}{t}^{\mathrm{2}} +{t}+\mathrm{4}{t}^{\mathrm{2}} −\mathrm{4}{t}+\mathrm{1} \\ $$$$−\mathrm{4}{t}^{\mathrm{3}} +\mathrm{3}{t}=\mathrm{4}{t}^{\mathrm{3}} −\mathrm{3}{t} \\ $$$${t}\left(\mathrm{8}{t}^{\mathrm{2}} −\mathrm{6}\right)=\mathrm{0}\Leftrightarrow{t}=\mathrm{0}\:\:\:{or}\:\:\:{t}^{\mathrm{2}} =\frac{\mathrm{3}}{\mathrm{4}} \\ $$$${t}=\mathrm{0}\:{or}\:\:{t}=\frac{\underset{−} {+}\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$${x}=\frac{\underset{−} {+}\pi}{\mathrm{2}}\:\:,\:\underset{−} {+}\frac{\pi}{\mathrm{6}}\:,\:\underset{−} {+}\frac{\mathrm{5}\pi}{\mathrm{6}} \\ $$$$\left({b}\right) \\ $$$$\mathrm{2}{sin}^{\mathrm{2}} {x}+{sin}^{\mathrm{2}} \left(\mathrm{2}{x}\right)−\mathrm{2}=\mathrm{0} \\ $$$$\mathrm{2}{sin}^{\mathrm{2}} {x}+\mathrm{4}{sin}^{\mathrm{2}} \left({x}\right){cos}^{\mathrm{2}} \left({x}\right)−\mathrm{2}=\mathrm{0} \\ $$$${sin}^{\mathrm{2}} {x}+\mathrm{2}{sin}^{\mathrm{2}} {x}\left(\mathrm{1}−{sin}^{\mathrm{2}} {x}\right)−\mathrm{1}=\mathrm{0} \\ $$$${sin}^{\mathrm{2}} {x}+\mathrm{2}{sin}^{\mathrm{2}} {x}−\mathrm{2}{sin}^{\mathrm{4}} {x}−\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{2}{sin}^{\mathrm{4}} {x}−\mathrm{3}{sin}^{\mathrm{2}} {x}+\mathrm{1}=\mathrm{0}\:\Leftrightarrow\:\left({sin}^{\mathrm{2}} {x}−\mathrm{1}\right)\left(\mathrm{2}{sin}^{\mathrm{2}} {x}−\mathrm{1}\right)=\mathrm{0} \\ $$$${sin}^{\mathrm{2}} {x}=\mathrm{1}\:\:{or}\:\:{sin}^{\mathrm{2}} {x}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${sinx}=\underset{−} {+}\mathrm{1}\:\:{or}\:{sinx}=\underset{−} {+}\frac{\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$$${x}=\underset{−} {+}\frac{\pi}{\mathrm{2}}\:,\:\underset{−} {+}\frac{\pi}{\mathrm{4}}\:,\:\underset{−} {+}\frac{\mathrm{3}\pi}{\mathrm{4}} \\ $$$$\left({c}\right) \\ $$$$\mathrm{3}{sinx}+\sqrt{\mathrm{3}{cosx}}=\mathrm{3} \\ $$$$\sqrt{\mathrm{3}{cosx}}=\mathrm{3}\left(\mathrm{1}−{sinx}\right) \\ $$$$\mathrm{3}{cosx}=\mathrm{9}\left(\mathrm{1}+{sin}^{\mathrm{2}} {x}−\mathrm{2}{sinx}\right)=\mathrm{9}\left(\mathrm{2}−{cos}^{\mathrm{2}} {x}−\mathrm{2}{sinx}\right) \\ $$$${cosx}=\mathrm{6}−\mathrm{3}{cos}^{\mathrm{2}} {x}−\mathrm{6}{sinx} \\ $$$$\mathrm{3}{cos}^{\mathrm{2}} {x}+{cosx}−\mathrm{6}=−\mathrm{6}{sinx} \\ $$$${let}\:\:{t}={cosx} \\ $$$$\mathrm{3}{t}^{\mathrm{2}} +{t}−\mathrm{6}=−\mathrm{6}\sqrt{\mathrm{1}−{t}^{\mathrm{2}} } \\ $$$$\left(\mathrm{3}{t}^{\mathrm{2}} +{t}−\mathrm{6}\right)^{\mathrm{2}} =\mathrm{36}−\mathrm{36}{t}^{\mathrm{2}} \\ $$$$\mathrm{9}{t}^{\mathrm{4}} +\mathrm{6}{t}^{\mathrm{2}} \left({t}−\mathrm{6}\right)+{t}^{\mathrm{2}} −\mathrm{12}{t}+\mathrm{36}=\mathrm{36}−\mathrm{36}{t}^{\mathrm{2}} \\ $$$$\mathrm{9}{t}^{\mathrm{4}} +\mathrm{6}{t}^{\mathrm{3}} −\mathrm{36}{t}^{\mathrm{2}} +{t}^{\mathrm{2}} −\mathrm{12}{t}=−\mathrm{36}{t}^{\mathrm{2}} \\ $$$$\mathrm{9}{t}^{\mathrm{4}} +\mathrm{6}{t}^{\mathrm{3}} +{t}^{\mathrm{2}} −\mathrm{12}{t}=\mathrm{0} \\ $$$${t}\left(\mathrm{9}{t}^{\mathrm{3}} +\mathrm{6}{t}^{\mathrm{2}} +{t}−\mathrm{12}\right)=\mathrm{0} \\ $$$$ \\ $$
Commented by myintkhaing last updated on 11/Jun/17
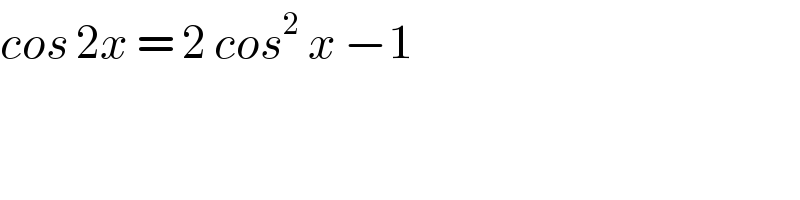
cos 2x = 2 cos^2 x −1
$${cos}\:\mathrm{2}{x}\:=\:\mathrm{2}\:{cos}^{\mathrm{2}} \:{x}\:−\mathrm{1} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *