Menu Close

Question-154851

Tinku Tara 0 Comments
Pin




Question Number 154851 by peter frank last updated on 22/Sep/21
Commented by peter frank last updated on 22/Sep/21
at U_o ^2 m/s .
$$\mathrm{at}\:\mathrm{U}_{\mathrm{o}} ^{\mathrm{2}} \:\mathrm{m}/\mathrm{s}\:. \\ $$
Commented by peter frank last updated on 22/Sep/21
A particle of mass M_o is tied to the string of length (L) and hang freely.if the particle displaced hanging (P) at U_o m/s.show that if particle complete a circle U_o ^2 ≥5gL
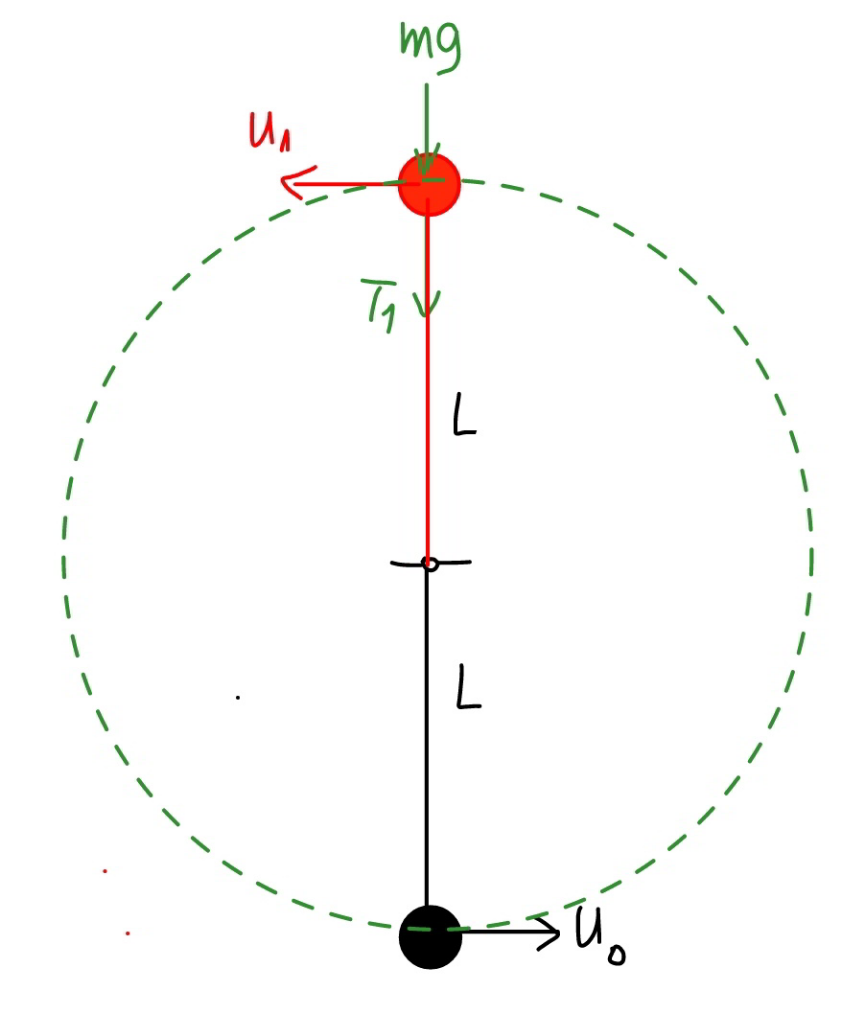
$$\mathrm{A}\:\mathrm{particle}\:\mathrm{of}\:\mathrm{mass}\:\mathrm{M}_{\mathrm{o}} \:\mathrm{is}\:\mathrm{tied}\:\mathrm{to} \\ $$$$\mathrm{the}\:\mathrm{string}\:\mathrm{of}\:\mathrm{length}\:\left(\mathrm{L}\right)\:\mathrm{and}\:\mathrm{hang} \\ $$$$\mathrm{freely}.\mathrm{if}\:\mathrm{the}\:\mathrm{particle}\:\mathrm{displaced} \\ $$$$\mathrm{hanging}\:\left(\mathrm{P}\right)\:\mathrm{at}\:\:\mathrm{U}_{\mathrm{o}} \mathrm{m}/\mathrm{s}.\mathrm{show}\:\mathrm{that} \\ $$$$\mathrm{if}\:\:\mathrm{particle}\:\mathrm{complete}\:\mathrm{a}\:\mathrm{circle} \\ $$$$\mathrm{U}_{\mathrm{o}} ^{\mathrm{2}} \geqslant\mathrm{5gL} \\ $$
Commented by mr W last updated on 23/Sep/21
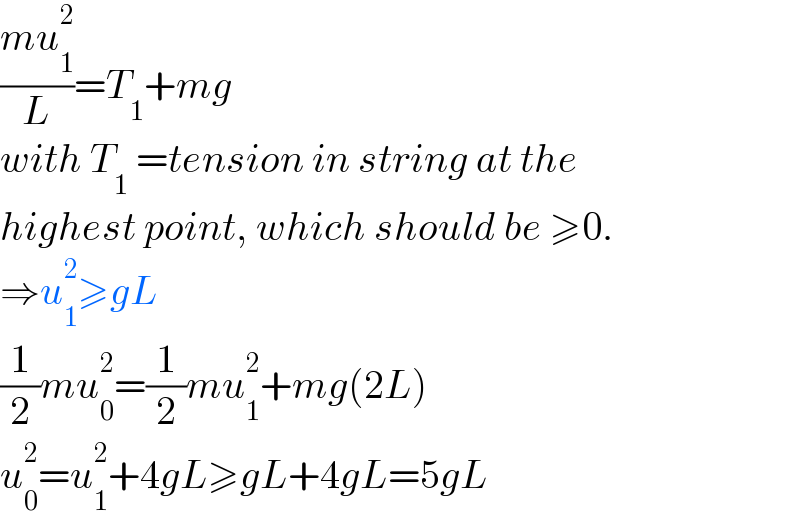
((mu_1 ^2 )/L)=T_1 +mg with T_1 =tension in string at the highest point, which should be ≥0. ⇒u_1 ^2 ≥gL (1/2)mu_0 ^2 =(1/2)mu_1 ^2 +mg(2L) u_0 ^2 =u_1 ^2 +4gL≥gL+4gL=5gL
$$\frac{{mu}_{\mathrm{1}} ^{\mathrm{2}} }{{L}}={T}_{\mathrm{1}} +{mg} \\ $$$${with}\:{T}_{\mathrm{1}} \:={tension}\:{in}\:{string}\:{at}\:{the} \\ $$$${highest}\:{point},\:{which}\:{should}\:{be}\:\geqslant\mathrm{0}. \\ $$$$\Rightarrow{u}_{\mathrm{1}} ^{\mathrm{2}} \geqslant{gL} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{mu}_{\mathrm{0}} ^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}{mu}_{\mathrm{1}} ^{\mathrm{2}} +{mg}\left(\mathrm{2}{L}\right) \\ $$$${u}_{\mathrm{0}} ^{\mathrm{2}} ={u}_{\mathrm{1}} ^{\mathrm{2}} +\mathrm{4}{gL}\geqslant{gL}+\mathrm{4}{gL}=\mathrm{5}{gL} \\ $$
Commented by mr W last updated on 23/Sep/21
Commented by peter frank last updated on 23/Sep/21
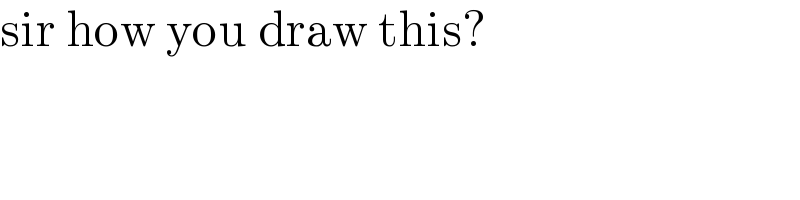
sir how you draw this?
$$\mathrm{sir}\:\mathrm{how}\:\mathrm{you}\:\mathrm{draw}\:\mathrm{this}?\: \\ $$
Commented by mr W last updated on 23/Sep/21
with no special app. i just used an app in my smart phone for foto editing.
$${with}\:{no}\:{special}\:{app}.\:{i}\:{just}\:{used}\:{an} \\ $$$${app}\:{in}\:{my}\:{smart}\:{phone}\:{for}\:{foto} \\ $$$${editing}. \\ $$
Commented by peter frank last updated on 23/Sep/21
From tha figure above Total energy at the bottom(E_b )= Total energy at Top(E_T ) E_B =E_T E_B =P.E_B +K.E_B E_B =m_o gh+(1/2)m_o u_o ^2 [h=0] E_B =(1/2)m_o u_o ^2 ....(i) E_T =P.E_B +K.E_B E_T =m_o gh_T +(1/2)m_o v_T E_T =m_o g(2l)+(1/2)m_o v_T E_T =(1/2)m_o V_T +2m_o gl ...(ii) E_B =E_T (1/2)m_o u_o ^2 =(1/2)m_o V_T ^2 +2m_o gl m_o V_T ^2 =m_o u_o ^2 −4m_o gl ....(iii) from T=((m_o V_T ^2 )/r)−mg for particle to complete the circle ((m_o V_T ^2 )/r)≥mg m_o V_T ^2 ≥mgr....(iv) m_o V_T ^2 =m_o u_o ^2 −4m_o gl...(iii) m_o u_o ^2 −4m_o gl≥m_o gr [r=l] m_o u_o ^2 ≥5m_o gl u_o ^2 ≥5gl
$$\mathrm{From}\:\mathrm{tha}\:\mathrm{figure}\:\mathrm{above}\: \\ $$$$\mathrm{Total}\:\mathrm{energy}\:\mathrm{at}\:\mathrm{the}\:\mathrm{bottom}\left(\mathrm{E}_{\mathrm{b}} \right)= \\ $$$$\mathrm{Total}\:\mathrm{energy}\:\mathrm{at}\:\:\mathrm{Top}\left(\mathrm{E}_{\mathrm{T}} \right) \\ $$$$\mathrm{E}_{\mathrm{B}} =\mathrm{E}_{\mathrm{T}} \\ $$$$\mathrm{E}_{\mathrm{B}} =\mathrm{P}.\mathrm{E}_{\mathrm{B}} +\mathrm{K}.\mathrm{E}_{\mathrm{B}} \\ $$$$\mathrm{E}_{\mathrm{B}} =\mathrm{m}_{\mathrm{o}} \mathrm{gh}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{m}_{\mathrm{o}} \mathrm{u}_{\mathrm{o}} ^{\mathrm{2}} \:\:\:\:\:\:\:\left[\mathrm{h}=\mathrm{0}\right] \\ $$$$\mathrm{E}_{\mathrm{B}} =\frac{\mathrm{1}}{\mathrm{2}}\mathrm{m}_{\mathrm{o}} \mathrm{u}_{\mathrm{o}} ^{\mathrm{2}} \:….\left(\mathrm{i}\right) \\ $$$$\mathrm{E}_{\mathrm{T}} =\mathrm{P}.\mathrm{E}_{\mathrm{B}} +\mathrm{K}.\mathrm{E}_{\mathrm{B}} \\ $$$$\mathrm{E}_{\mathrm{T}} =\mathrm{m}_{\mathrm{o}} \mathrm{gh}_{\mathrm{T}} +\frac{\mathrm{1}}{\mathrm{2}}\mathrm{m}_{\mathrm{o}} \mathrm{v}_{\mathrm{T}} \\ $$$$\mathrm{E}_{\mathrm{T}} =\mathrm{m}_{\mathrm{o}} \mathrm{g}\left(\mathrm{2l}\right)+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{m}_{\mathrm{o}} \mathrm{v}_{\mathrm{T}} \\ $$$$\mathrm{E}_{\mathrm{T}} =\frac{\mathrm{1}}{\mathrm{2}}\mathrm{m}_{\mathrm{o}} \mathrm{V}_{\mathrm{T}} +\mathrm{2m}_{\mathrm{o}} \mathrm{gl}\:\:\:…\left(\mathrm{ii}\right) \\ $$$$\mathrm{E}_{\mathrm{B}} =\mathrm{E}_{\mathrm{T}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\mathrm{m}_{\mathrm{o}} \mathrm{u}_{\mathrm{o}} ^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}\mathrm{m}_{\mathrm{o}} \mathrm{V}_{\mathrm{T}} ^{\mathrm{2}} +\mathrm{2m}_{\mathrm{o}} \mathrm{gl} \\ $$$$\mathrm{m}_{\mathrm{o}} \mathrm{V}_{\mathrm{T}} ^{\mathrm{2}} =\mathrm{m}_{\mathrm{o}} \mathrm{u}_{\mathrm{o}} ^{\mathrm{2}} −\mathrm{4m}_{\mathrm{o}} \mathrm{gl}\:\:….\left(\mathrm{iii}\right) \\ $$$$\mathrm{from} \\ $$$$\mathrm{T}=\frac{\mathrm{m}_{\mathrm{o}} \mathrm{V}_{\mathrm{T}} ^{\mathrm{2}} }{\mathrm{r}}−\mathrm{mg} \\ $$$$\mathrm{for}\:\mathrm{particle}\:\mathrm{to}\:\mathrm{complete}\:\mathrm{the}\:\mathrm{circle} \\ $$$$\frac{\mathrm{m}_{\mathrm{o}} \mathrm{V}_{\mathrm{T}} ^{\mathrm{2}} }{\mathrm{r}}\geqslant\mathrm{mg} \\ $$$$\mathrm{m}_{\mathrm{o}} \mathrm{V}_{\mathrm{T}} ^{\mathrm{2}} \geqslant\mathrm{mgr}….\left(\mathrm{iv}\right) \\ $$$$\mathrm{m}_{\mathrm{o}} \mathrm{V}_{\mathrm{T}} ^{\mathrm{2}} =\mathrm{m}_{\mathrm{o}} \mathrm{u}_{\mathrm{o}} ^{\mathrm{2}} −\mathrm{4m}_{\mathrm{o}} \mathrm{gl}…\left(\mathrm{iii}\right) \\ $$$$\mathrm{m}_{\mathrm{o}} \mathrm{u}_{\mathrm{o}} ^{\mathrm{2}} −\mathrm{4m}_{\mathrm{o}} \mathrm{gl}\geqslant\mathrm{m}_{\mathrm{o}} \mathrm{gr}\:\:\:\left[\mathrm{r}=\mathrm{l}\right] \\ $$$$\mathrm{m}_{\mathrm{o}} \mathrm{u}_{\mathrm{o}} ^{\mathrm{2}} \geqslant\mathrm{5m}_{\mathrm{o}} \mathrm{g}{l} \\ $$$$\mathrm{u}_{\mathrm{o}} ^{\mathrm{2}} \geqslant\mathrm{5g}{l} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *