Question Number 154875 by mathdanisur last updated on 22/Sep/21

Answered by mindispower last updated on 23/Sep/21

$${u}={log}\left({x}+\frac{\mathrm{5}}{{x}}\right) \\ $$$$\Omega\Leftrightarrow\int{e}^{\mathrm{2}{u}} {sin}\left({u}\right){du} \\ $$
Commented by mathdanisur last updated on 23/Sep/21

$$\mathrm{thanks}\:\boldsymbol{\mathrm{S}}\mathrm{er},\:\mathrm{but}\:\mathrm{how} \\ $$
Commented by mindispower last updated on 23/Sep/21
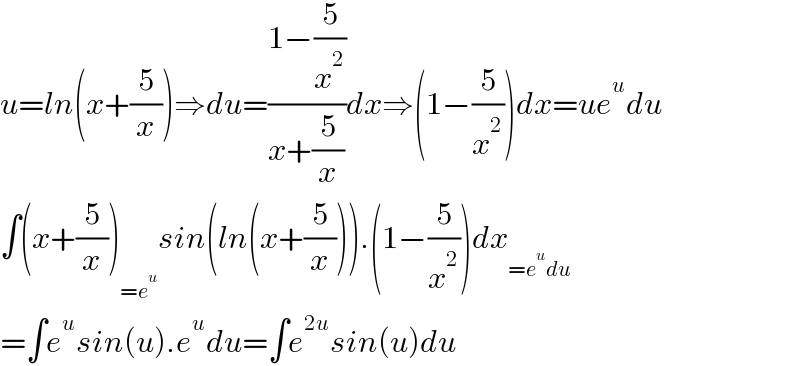
$${u}={ln}\left({x}+\frac{\mathrm{5}}{{x}}\right)\Rightarrow{du}=\frac{\mathrm{1}−\frac{\mathrm{5}}{{x}^{\mathrm{2}} }}{{x}+\frac{\mathrm{5}}{{x}}}{dx}\Rightarrow\left(\mathrm{1}−\frac{\mathrm{5}}{{x}^{\mathrm{2}} }\right){dx}={ue}^{{u}} {du} \\ $$$$\int\left({x}+\frac{\mathrm{5}}{{x}}\right)_{={e}^{{u}} } {sin}\left({ln}\left({x}+\frac{\mathrm{5}}{{x}}\right)\right).\left(\mathrm{1}−\frac{\mathrm{5}}{{x}^{\mathrm{2}} }\right){dx}_{={e}^{{u}} {du}} \\ $$$$=\int{e}^{{u}} {sin}\left({u}\right).{e}^{{u}} {du}=\int{e}^{\mathrm{2}{u}} {sin}\left({u}\right){du} \\ $$
Commented by mathdanisur last updated on 23/Sep/21

$$\mathrm{very}\:\mathrm{nise}\:\boldsymbol{\mathrm{S}}\mathrm{er},\:\mathrm{thank}\:\mathrm{you} \\ $$
Commented by mindispower last updated on 23/Sep/21

$${withe}\:{Pleasur} \\ $$
