Question Number 154880 by saly last updated on 22/Sep/21
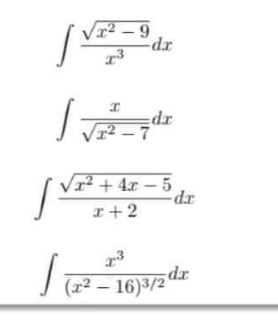
Answered by Ar Brandon last updated on 22/Sep/21
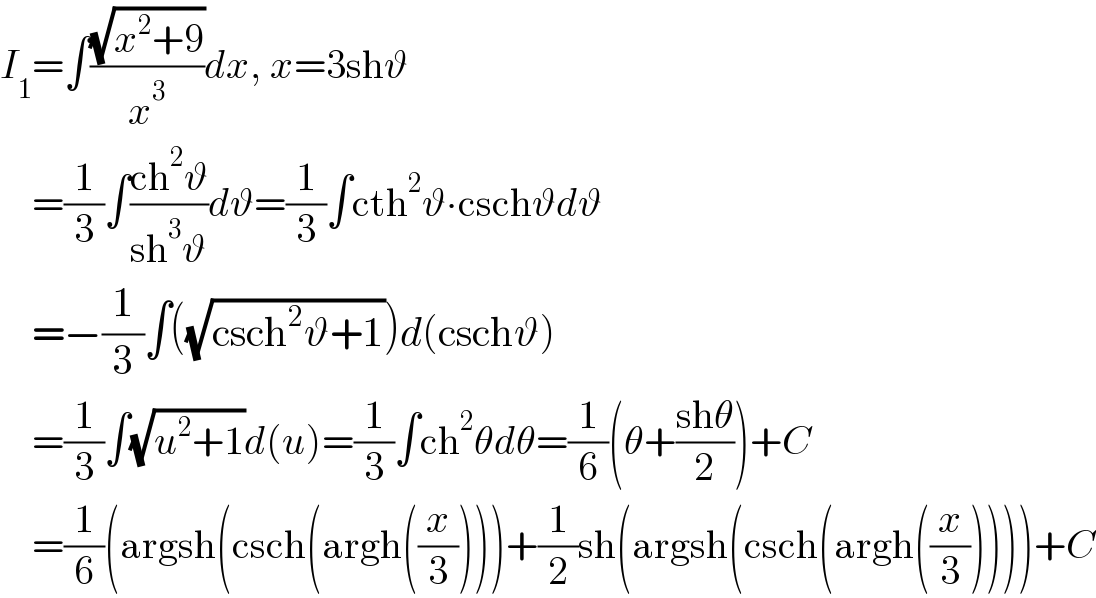
$${I}_{\mathrm{1}} =\int\frac{\sqrt{{x}^{\mathrm{2}} +\mathrm{9}}}{{x}^{\mathrm{3}} }{dx},\:{x}=\mathrm{3sh}\vartheta \\ $$$$\:\:\:\:=\frac{\mathrm{1}}{\mathrm{3}}\int\frac{\mathrm{ch}^{\mathrm{2}} \vartheta}{\mathrm{sh}^{\mathrm{3}} \vartheta}{d}\vartheta=\frac{\mathrm{1}}{\mathrm{3}}\int\mathrm{cth}^{\mathrm{2}} \vartheta\centerdot\mathrm{csch}\vartheta{d}\vartheta \\ $$$$\:\:\:\:=−\frac{\mathrm{1}}{\mathrm{3}}\int\left(\sqrt{\mathrm{csch}^{\mathrm{2}} \vartheta+\mathrm{1}}\right){d}\left(\mathrm{csch}\vartheta\right) \\ $$$$\:\:\:\:=\frac{\mathrm{1}}{\mathrm{3}}\int\sqrt{{u}^{\mathrm{2}} +\mathrm{1}}{d}\left({u}\right)=\frac{\mathrm{1}}{\mathrm{3}}\int\mathrm{ch}^{\mathrm{2}} \theta{d}\theta=\frac{\mathrm{1}}{\mathrm{6}}\left(\theta+\frac{\mathrm{sh}\theta}{\mathrm{2}}\right)+{C} \\ $$$$\:\:\:\:=\frac{\mathrm{1}}{\mathrm{6}}\left(\mathrm{argsh}\left(\mathrm{csch}\left(\mathrm{argh}\left(\frac{{x}}{\mathrm{3}}\right)\right)\right)+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sh}\left(\mathrm{argsh}\left(\mathrm{csch}\left(\mathrm{argh}\left(\frac{{x}}{\mathrm{3}}\right)\right)\right)\right)+{C}\right. \\ $$
Answered by maged last updated on 23/Sep/21
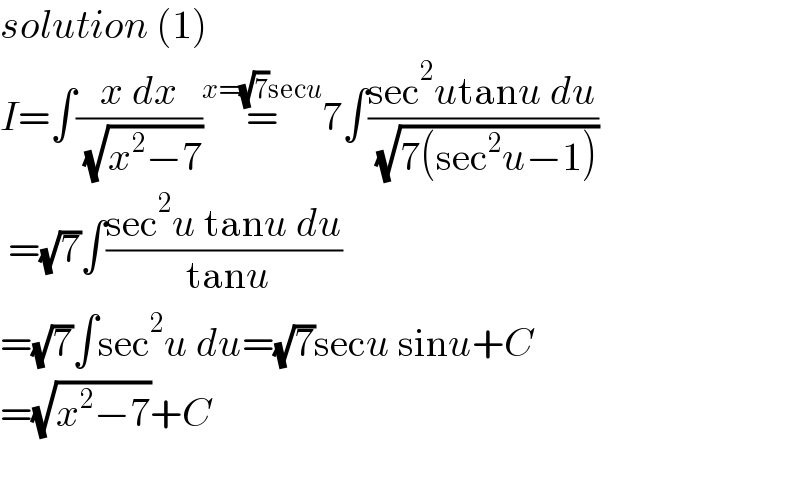
$${solution}\:\left(\mathrm{1}\right) \\ $$$${I}=\int\frac{{x}\:{dx}}{\:\sqrt{{x}^{\mathrm{2}} −\mathrm{7}}}\overset{{x}=\sqrt{\mathrm{7}}\mathrm{sec}{u}} {=}\mathrm{7}\int\frac{\mathrm{sec}^{\mathrm{2}} {u}\mathrm{tan}{u}\:{du}}{\:\sqrt{\mathrm{7}\left(\mathrm{sec}^{\mathrm{2}} {u}−\mathrm{1}\right)}} \\ $$$$\:=\sqrt{\mathrm{7}}\int\frac{\mathrm{sec}^{\mathrm{2}} {u}\:\mathrm{tan}{u}\:{du}}{\:\mathrm{tan}{u}} \\ $$$$=\sqrt{\mathrm{7}}\int\mathrm{sec}^{\mathrm{2}} {u}\:{du}=\sqrt{\mathrm{7}}\mathrm{sec}{u}\:\mathrm{sin}{u}+{C} \\ $$$$=\sqrt{{x}^{\mathrm{2}} −\mathrm{7}}+{C} \\ $$$$ \\ $$
Answered by Ar Brandon last updated on 23/Sep/21

$${I}_{\mathrm{1}} =\int\frac{\sqrt{{x}^{\mathrm{2}} −\mathrm{9}}}{{x}^{\mathrm{3}} }{dx},\:{x}=\mathrm{3sec}\vartheta\Rightarrow{dx}=\mathrm{3sec}\vartheta\mathrm{tan}\vartheta{d}\vartheta \\ $$$$\:\:\:\:=\frac{\mathrm{1}}{\mathrm{3}}\int\frac{\mathrm{tan}^{\mathrm{2}} \vartheta}{\mathrm{sec}^{\mathrm{2}} \vartheta}{d}\vartheta=\frac{\mathrm{1}}{\mathrm{3}}\int\mathrm{sin}^{\mathrm{2}} \vartheta{d}\vartheta=\frac{\mathrm{1}}{\mathrm{6}}\left(\vartheta−\frac{\mathrm{sin2}\vartheta}{\mathrm{2}}\right)+\mathrm{C} \\ $$$$\:\:\:\:=\frac{\mathrm{1}}{\mathrm{6}}\left(\mathrm{sec}^{−\mathrm{1}} \left(\frac{{x}}{\mathrm{3}}\right)−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\left(\mathrm{2sec}^{−\mathrm{1}} \left(\frac{{x}}{\mathrm{3}}\right)\right)\right)+{C} \\ $$$$ \\ $$$${I}_{\mathrm{2}} =\int\frac{{x}}{\:\sqrt{{x}^{\mathrm{2}} −\mathrm{7}}}{dx}=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{2}{x}}{\:\sqrt{{x}^{\mathrm{2}} −\mathrm{7}}}{dx} \\ $$$$\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{d}\left({x}^{\mathrm{2}} −\mathrm{7}\right)}{\:\sqrt{{x}^{\mathrm{2}} −\mathrm{7}}}=\sqrt{{x}^{\mathrm{2}} −\mathrm{7}}+{C}_{\mathrm{2}} \\ $$$$ \\ $$$${I}_{\mathrm{3}} =\int\frac{\sqrt{{x}^{\mathrm{2}} +\mathrm{4}{x}−\mathrm{5}}}{{x}+\mathrm{2}}{dx}=\int\frac{\sqrt{\left({x}+\mathrm{2}\right)^{\mathrm{2}} −\mathrm{9}}}{{x}+\mathrm{2}}{dx},\:{x}+\mathrm{2}=\mathrm{3sec}\vartheta \\ $$$$\:\:\:\:=\mathrm{3}\int\mathrm{tan}^{\mathrm{2}} \vartheta{d}\vartheta=\mathrm{3}\int\left(\mathrm{sec}^{\mathrm{2}} \vartheta−\mathrm{1}\right){d}\vartheta=\mathrm{3}\left(\mathrm{tan}\vartheta−\vartheta\right)+\mathrm{C} \\ $$$$\:\:\:\:=\mathrm{3}\left(\mathrm{tan}\left(\mathrm{sec}^{−\mathrm{1}} \left(\frac{{x}+\mathrm{2}}{\mathrm{3}}\right)\right)−\mathrm{sec}^{−\mathrm{1}} \left(\frac{{x}+\mathrm{2}}{\mathrm{3}}\right)\right)+{C}_{\mathrm{3}} \\ $$$$ \\ $$$${I}_{\mathrm{4}} =\int\frac{{x}^{\mathrm{3}} }{\left({x}^{\mathrm{2}} −\mathrm{16}\right)^{\mathrm{3}/\mathrm{2}} }{dx},\:{x}=\mathrm{4sec}\vartheta\Rightarrow{dx}=\mathrm{4sec}\vartheta\mathrm{tan}\vartheta \\ $$$$\:\:\:\:=\int\frac{\mathrm{64sec}^{\mathrm{3}} \vartheta\centerdot\mathrm{4sec}\vartheta\mathrm{tan}\vartheta}{\left(\mathrm{16sec}^{\mathrm{2}} \vartheta−\mathrm{16}\right)^{\mathrm{3}/\mathrm{2}} }{d}\vartheta=\mathrm{4}\int\frac{\mathrm{sec}^{\mathrm{4}} \vartheta\mathrm{tan}\vartheta}{\mathrm{tan}^{\mathrm{3}} \vartheta}{d}\vartheta \\ $$$$\:\:\:\:=\mathrm{4}\int\frac{\mathrm{sec}^{\mathrm{4}} \vartheta}{\mathrm{tan}^{\mathrm{2}} \vartheta}{d}\vartheta=\mathrm{4}\int\frac{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \vartheta}{\mathrm{tan}^{\mathrm{2}} \vartheta}{d}\left(\mathrm{tan}\vartheta\right) \\ $$$$\:\:\:\:=\mathrm{4}\left(\mathrm{tan}\vartheta−\frac{\mathrm{1}}{\mathrm{tan}\vartheta}\right)+{C}=\mathrm{4}\left(\mathrm{tan}\left(\mathrm{sec}^{−\mathrm{1}} \left(\frac{{x}}{\mathrm{4}}\right)\right)+\mathrm{cot}\left(\mathrm{sec}^{−\mathrm{1}} \left(\frac{{x}}{\mathrm{4}}\right)\right)\right)+{C}_{\mathrm{4}} \\ $$
Commented by saly last updated on 24/Sep/21

$$\:{thank}\:{you} \\ $$
Answered by maged last updated on 23/Sep/21
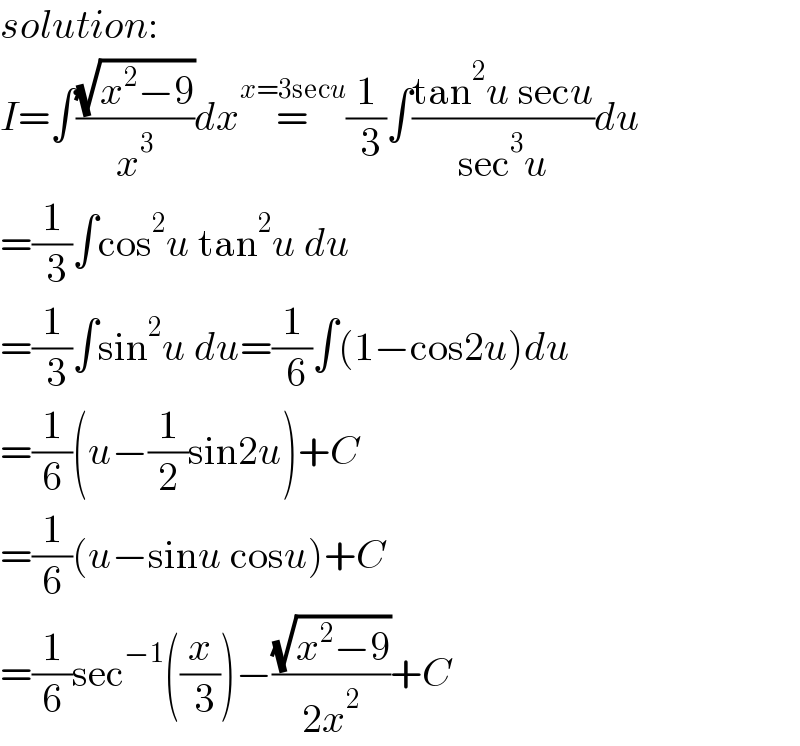
$${solution}: \\ $$$${I}=\int\frac{\sqrt{{x}^{\mathrm{2}} −\mathrm{9}}}{{x}^{\mathrm{3}} }{dx}\overset{{x}=\mathrm{3sec}{u}} {=}\frac{\mathrm{1}}{\:\mathrm{3}}\int\frac{\mathrm{tan}^{\mathrm{2}} {u}\:\mathrm{sec}{u}}{\mathrm{sec}^{\mathrm{3}} {u}}{du} \\ $$$$=\frac{\mathrm{1}}{\:\mathrm{3}}\int\mathrm{cos}^{\mathrm{2}} {u}\:\mathrm{tan}^{\mathrm{2}} {u}\:{du} \\ $$$$=\frac{\mathrm{1}}{\:\mathrm{3}}\int\mathrm{sin}^{\mathrm{2}} {u}\:{du}=\frac{\mathrm{1}}{\:\mathrm{6}}\int\left(\mathrm{1}−\mathrm{cos2}{u}\right){du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\left({u}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin2}{u}\right)+{C} \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\left({u}−\mathrm{sin}{u}\:\mathrm{cos}{u}\right)+{C} \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\mathrm{sec}^{−\mathrm{1}} \left(\frac{{x}}{\:\mathrm{3}}\right)−\frac{\sqrt{{x}^{\mathrm{2}} −\mathrm{9}}}{\mathrm{2}{x}^{\mathrm{2}} }+{C} \\ $$
Answered by maged last updated on 23/Sep/21

$${I}_{\mathrm{3}} =\int\frac{\sqrt{{x}^{\mathrm{2}} +\mathrm{4}{x}−\mathrm{5}}}{{x}+\mathrm{2}}{dx} \\ $$$${solution}: \\ $$$${I}_{\mathrm{3}} =\int\frac{\sqrt{{x}^{\mathrm{2}} +\mathrm{4}{x}−\mathrm{5}}}{{x}+\mathrm{2}}{dx} \\ $$$$=\int\frac{\sqrt{{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{4}−\mathrm{9}}}{{x}+\mathrm{2}}{dx} \\ $$$$=\int\frac{\sqrt{\left({x}+\mathrm{2}\right)^{\mathrm{2}} −\mathrm{9}}}{{x}+\mathrm{2}}{dx}\overset{{x}+\mathrm{2}=\mathrm{3sec}{u}} {=}\int\frac{\sqrt{\mathrm{9}\left(\mathrm{sec}^{\mathrm{2}} {u}−\mathrm{1}\right)}}{\mathrm{3sec}{u}}\mathrm{3sec}{u}\:\mathrm{tan}{u}\:{du} \\ $$$$=\mathrm{3}\int\mathrm{tan}^{\mathrm{2}} {u}\:{du}=\mathrm{3}\int\left(\mathrm{sec}^{\mathrm{2}} {u}−\mathrm{1}\right){du} \\ $$$$=\mathrm{3tan}{u}−\mathrm{3}{u}+{C} \\ $$$$=\sqrt{\left({x}+\mathrm{2}\right)^{\mathrm{2}} −\mathrm{9}}\:−\mathrm{3sec}^{−\mathrm{1}} \left(\frac{{x}+\mathrm{2}}{\mathrm{3}}\right)+{C} \\ $$$$=\sqrt{{x}^{\mathrm{2}} +\mathrm{4}{x}−\mathrm{5}}\:−\mathrm{3sec}^{−\mathrm{1}} \left(\frac{{x}+\mathrm{2}}{\mathrm{3}}\right)+{C} \\ $$$$ \\ $$
Commented by saly last updated on 24/Sep/21

$$\:{thank}\:{you} \\ $$
Answered by maged last updated on 23/Sep/21

$${I}_{\mathrm{4}} =\int\frac{{x}^{\mathrm{3}} }{\:\sqrt{\left({x}^{\mathrm{2}} −\mathrm{16}\right)^{\mathrm{3}} }}{dx} \\ $$$${solution}: \\ $$$${I}=\int\frac{{x}^{\mathrm{3}} }{\:\sqrt{\left({x}^{\mathrm{2}} −\mathrm{16}\right)^{\mathrm{3}} }}{dx}\overset{{x}=\mathrm{4sec}{u}} {=}\int\frac{\mathrm{64sec}^{\mathrm{3}} {u}\:}{\:\sqrt{\mathrm{16}^{\mathrm{3}} \left(\mathrm{sec}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{3}} }}\mathrm{4sec}{u}\:\mathrm{tan}{u}\:{du}\:\: \\ $$$$=\mathrm{4}^{\mathrm{3}} \int\frac{\mathrm{sec}^{\mathrm{3}} {u}\:}{\:\mathrm{4}^{\mathrm{3}} \mathrm{tan}^{\mathrm{3}} {u}}\mathrm{4sec}{u}\:\mathrm{tan}{u}\:{du}\:\: \\ $$$$=\mathrm{4}\int\frac{\mathrm{sec}^{\mathrm{4}} {u}}{\mathrm{tan}^{\mathrm{2}} {u}}\:{du}\:=\mathrm{4}\int\frac{\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} {u}\right)^{\mathrm{2}} }{\mathrm{tan}^{\mathrm{2}} {u}}{du} \\ $$$$=\mathrm{4}\int\left(\frac{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} {u}}{\mathrm{tan}{u}}\right)^{\mathrm{2}} {du}=\mathrm{4}\int\left(\frac{\mathrm{1}}{\mathrm{tan}\:{u}}+\mathrm{tan}{u}\right)^{\mathrm{2}} {du} \\ $$$$=\mathrm{4}\int\left(\mathrm{cot}^{\mathrm{2}} {u}+\mathrm{2}+\mathrm{tan}^{\mathrm{2}} {u}\right){du} \\ $$$$=\mathrm{4}\int\left(\mathrm{cosec}^{\mathrm{2}} {u}−\mathrm{1}+\mathrm{sec}^{\mathrm{2}} {u}−\mathrm{1}+\mathrm{2}\right){du} \\ $$$$=\mathrm{4}\int\left(\mathrm{sec}^{\mathrm{2}} {u}+\mathrm{cosec}^{\mathrm{2}} {u}\right){du} \\ $$$$=\mathrm{4tan}{u}−\mathrm{4cot}{u}+{C} \\ $$$$\because{x}=\mathrm{4sec}{u}\rightarrow\mathrm{tan}{u}=\frac{\mathrm{1}}{\mathrm{4}}\sqrt{{x}^{\mathrm{2}} −\mathrm{16}} \\ $$$$\mathrm{cot}{u}=\frac{\mathrm{4}}{\:\sqrt{{x}^{\mathrm{2}} −\mathrm{16}}} \\ $$$${I}=\sqrt{{x}^{\mathrm{2}} −\mathrm{16}−}\frac{\mathrm{16}}{\:\sqrt{{x}^{\mathrm{2}} −\mathrm{16}}}+{C} \\ $$
