Question Number 154888 by physicstutes last updated on 22/Sep/21

Answered by mr W last updated on 23/Sep/21

Commented by physicstutes last updated on 23/Sep/21
$$\mathrm{brilliant}\:\mathrm{sir}\:\mathrm{thanks} \\ $$
Commented by mr W last updated on 23/Sep/21
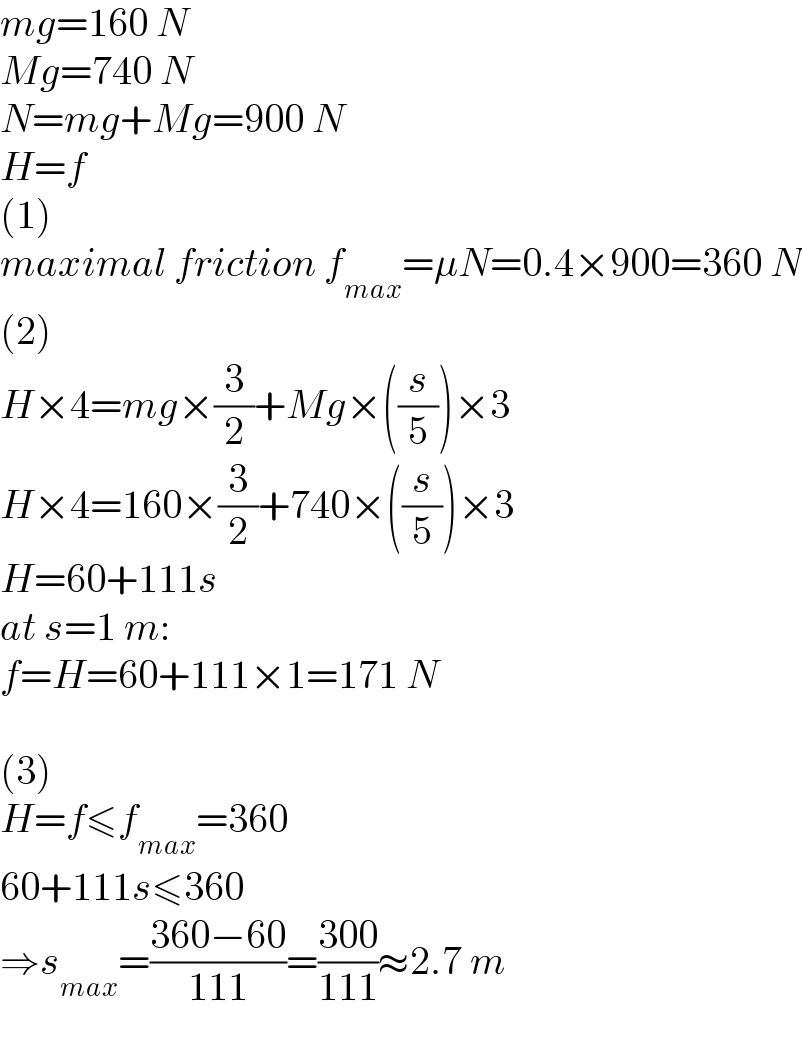
$${mg}=\mathrm{160}\:{N} \\ $$$${Mg}=\mathrm{740}\:{N} \\ $$$${N}={mg}+{Mg}=\mathrm{900}\:{N} \\ $$$${H}={f} \\ $$$$\left(\mathrm{1}\right) \\ $$$${maximal}\:{friction}\:{f}_{{max}} =\mu{N}=\mathrm{0}.\mathrm{4}×\mathrm{900}=\mathrm{360}\:{N} \\ $$$$\left(\mathrm{2}\right) \\ $$$${H}×\mathrm{4}={mg}×\frac{\mathrm{3}}{\mathrm{2}}+{Mg}×\left(\frac{{s}}{\mathrm{5}}\right)×\mathrm{3} \\ $$$${H}×\mathrm{4}=\mathrm{160}×\frac{\mathrm{3}}{\mathrm{2}}+\mathrm{740}×\left(\frac{{s}}{\mathrm{5}}\right)×\mathrm{3} \\ $$$${H}=\mathrm{60}+\mathrm{111}{s} \\ $$$${at}\:{s}=\mathrm{1}\:{m}: \\ $$$${f}={H}=\mathrm{60}+\mathrm{111}×\mathrm{1}=\mathrm{171}\:{N} \\ $$$$ \\ $$$$\left(\mathrm{3}\right) \\ $$$${H}={f}\leqslant{f}_{{max}} =\mathrm{360} \\ $$$$\mathrm{60}+\mathrm{111}{s}\leqslant\mathrm{360} \\ $$$$\Rightarrow{s}_{{max}} =\frac{\mathrm{360}−\mathrm{60}}{\mathrm{111}}=\frac{\mathrm{300}}{\mathrm{111}}\approx\mathrm{2}.\mathrm{7}\:{m} \\ $$
Commented by Tawa11 last updated on 23/Sep/21

$$\mathrm{great}\:\mathrm{sir} \\ $$
