Question Number 155034 by peter frank last updated on 24/Sep/21
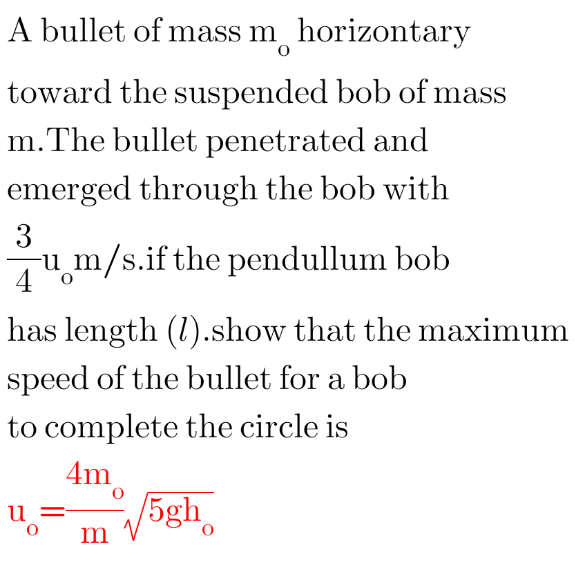
Commented by peter frank last updated on 24/Sep/21
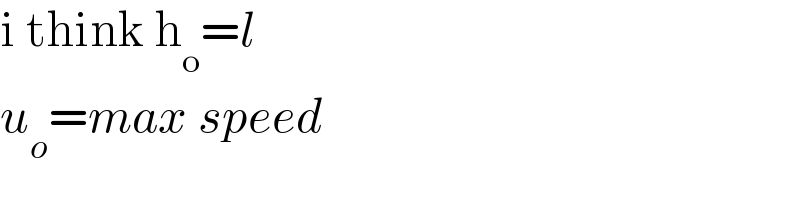
$$\mathrm{i}\:\mathrm{think}\:\mathrm{h}_{\mathrm{o}} ={l} \\ $$$${u}_{{o}} ={max}\:{speed} \\ $$
Commented by mr W last updated on 24/Sep/21

$${please}\:{check}\:{your}\:{typos}! \\ $$$${what}\:{is}\:{h}_{\mathrm{0}} ?,\:{what}\:{is}\:{u}_{\mathrm{0}} ?,\:{maximum} \\ $$$${speed}\:{or}\:{minimum}\:{speed}? \\ $$
Commented by mr W last updated on 24/Sep/21

$${no}.\:{that}\:{is}\:{the}\:{minimum}\:{speed}\:{the} \\ $$$${bullet}\:{must}\:{have}.\:{if}\:{the}\:{speed}\:{is}\:{less} \\ $$$${than}\:{it},\:{the}\:{bob}\:{can}\:{not}\:{complete}\:{a} \\ $$$${circle}. \\ $$
Commented by mr W last updated on 24/Sep/21
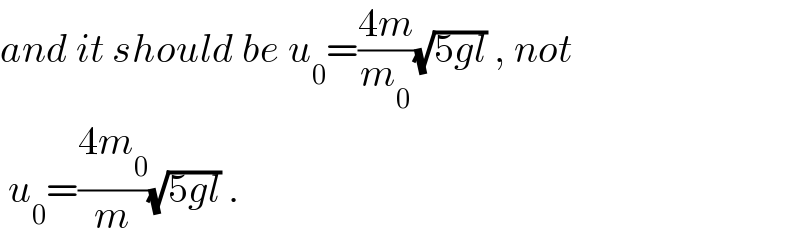
$${and}\:{it}\:{should}\:{be}\:{u}_{\mathrm{0}} =\frac{\mathrm{4}{m}}{{m}_{\mathrm{0}} }\sqrt{\mathrm{5}{gl}}\:,\:{not} \\ $$$$\:{u}_{\mathrm{0}} =\frac{\mathrm{4}{m}_{\mathrm{0}} }{{m}}\sqrt{\mathrm{5}{gl}}\:. \\ $$
Answered by mr W last updated on 24/Sep/21
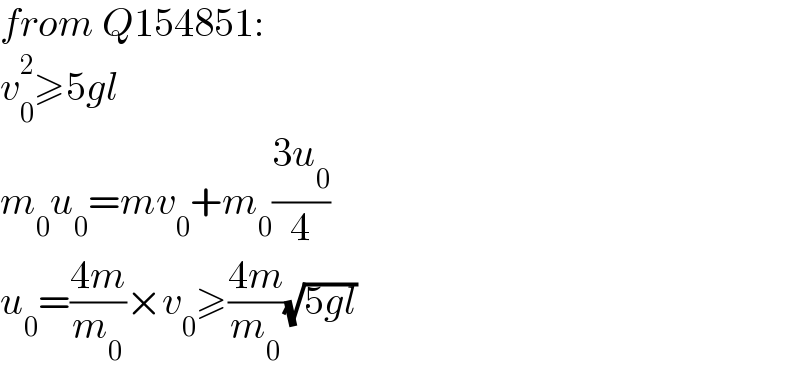
$${from}\:{Q}\mathrm{154851}: \\ $$$${v}_{\mathrm{0}} ^{\mathrm{2}} \geqslant\mathrm{5}{gl} \\ $$$${m}_{\mathrm{0}} {u}_{\mathrm{0}} ={mv}_{\mathrm{0}} +{m}_{\mathrm{0}} \frac{\mathrm{3}{u}_{\mathrm{0}} }{\mathrm{4}} \\ $$$${u}_{\mathrm{0}} =\frac{\mathrm{4}{m}}{{m}_{\mathrm{0}} }×{v}_{\mathrm{0}} \geqslant\frac{\mathrm{4}{m}}{{m}_{\mathrm{0}} }\sqrt{\mathrm{5}{gl}} \\ $$
Answered by peter frank last updated on 25/Sep/21

Commented by peter frank last updated on 25/Sep/21
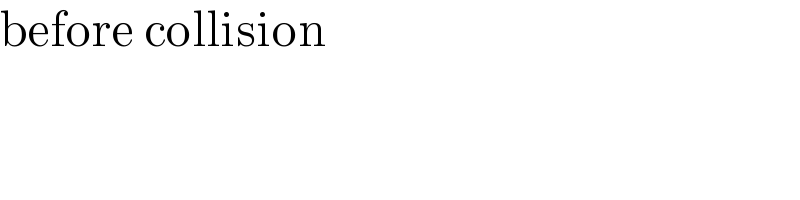
$$\mathrm{before}\:\mathrm{collision} \\ $$
Answered by peter frank last updated on 25/Sep/21
Commented by peter frank last updated on 25/Sep/21

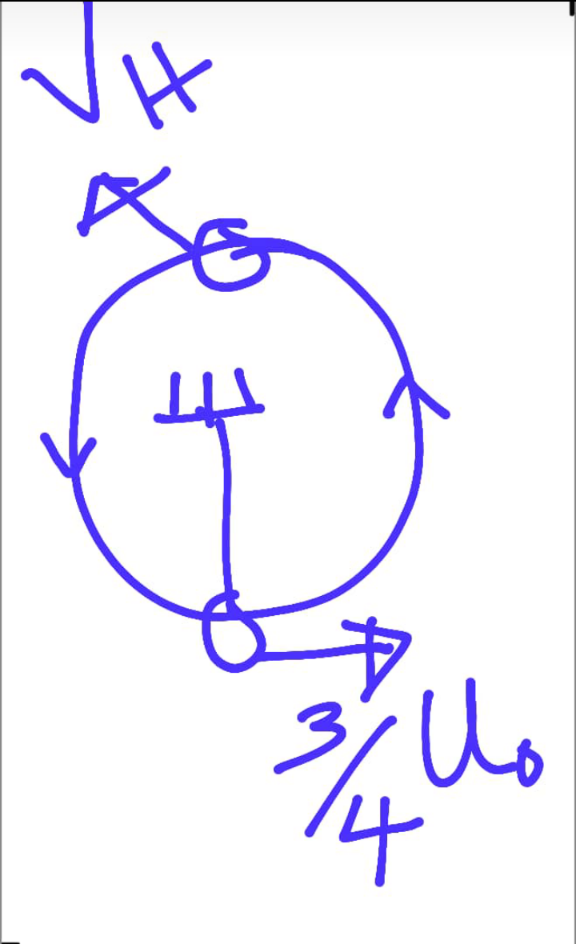
$$\mathrm{after}\:\mathrm{collision} \\ $$
Commented by peter frank last updated on 25/Sep/21
![since there are collision, momentum is conserved Momentum before collisio(M_(bc) )= Momentum after collision(M_(apc) )= u_o m_o +m_B u_B =(3/4)m_o u_o +Mv_B u_B =0 v_B =((m_o u_o )/(4M)) ...(i) Total Energy at the bottom= Total Energy at the Top(highest) E_B =E_T K.E_B +P.E_B =K.E_H +P.E_H (1/2)Mv_o ^2 +mg(0)=(1/2)Mv_H ^2 +mg(l+l) v_B ^2 =v_H ^2 +4gl ....(ii) (((m_o u_o )/(4M)) )^2 =V_H ^2 +4gl v_H ^2 =((m_o ^2 u_o ^2 )/(16M)) −4gl .....(iii) for any particle to complete a circle safely ((mv_H ^2 )/r)>mg (v_H ^2 /r)>g v_H ^2 >gr .....(iv) ((m_o ^2 u_o ^2 )/(16M)) −4gl >gr [r=l] ((m_o ^2 u_o ^2 )/(16M)) >5gl m_o ^2 u_o ^2 >80Mgl u_o >((√(80Mgl))/m_o ) u_o >((4M(√(5gl)))/m_o ) u_o =((4M(√(5gl)))/m_o )](https://www.tinkutara.com/question/Q155095.png)
$$\mathrm{since}\:\mathrm{there}\:\mathrm{are}\:\mathrm{collision}, \\ $$$$\mathrm{momentum}\:\mathrm{is}\:\mathrm{conserved} \\ $$$$\mathrm{Momentum}\:\mathrm{before}\:\mathrm{collisio}\left(\mathrm{M}_{\mathrm{bc}} \right)= \\ $$$$\mathrm{Momentum}\:\mathrm{after}\:\:\mathrm{collision}\left(\mathrm{M}_{\mathrm{apc}} \right)= \\ $$$$\mathrm{u}_{\mathrm{o}} \mathrm{m}_{\mathrm{o}} +\mathrm{m}_{\mathrm{B}} \mathrm{u}_{\mathrm{B}} =\frac{\mathrm{3}}{\mathrm{4}}\mathrm{m}_{\mathrm{o}} \mathrm{u}_{\mathrm{o}} +\mathrm{Mv}_{\mathrm{B}} \\ $$$$\mathrm{u}_{\mathrm{B}} =\mathrm{0} \\ $$$$\mathrm{v}_{\mathrm{B}} =\frac{\mathrm{m}_{\mathrm{o}} \mathrm{u}_{\mathrm{o}} }{\mathrm{4M}}\:\:\:…\left(\mathrm{i}\right) \\ $$$$\mathrm{Total}\:\mathrm{Energy}\:\mathrm{at}\:\mathrm{the}\:\mathrm{bottom}= \\ $$$$\mathrm{Total}\:\mathrm{Energy}\:\mathrm{at}\:\mathrm{the}\:\mathrm{Top}\left(\mathrm{highest}\right) \\ $$$$\mathrm{E}_{\mathrm{B}} =\mathrm{E}_{\mathrm{T}} \\ $$$$\mathrm{K}.\mathrm{E}_{\mathrm{B}} +\mathrm{P}.\mathrm{E}_{\mathrm{B}} =\mathrm{K}.\mathrm{E}_{\mathrm{H}} +\mathrm{P}.\mathrm{E}_{\mathrm{H}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\mathrm{Mv}_{\mathrm{o}} ^{\mathrm{2}} +\mathrm{mg}\left(\mathrm{0}\right)=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{Mv}_{\mathrm{H}} ^{\mathrm{2}} +\mathrm{mg}\left({l}+{l}\right) \\ $$$$\mathrm{v}_{\mathrm{B}} ^{\mathrm{2}} =\mathrm{v}_{\mathrm{H}} ^{\mathrm{2}} +\mathrm{4g}{l}\:\:….\left(\mathrm{ii}\right) \\ $$$$\left(\frac{\mathrm{m}_{\mathrm{o}} \mathrm{u}_{\mathrm{o}} }{\mathrm{4M}}\:\right)^{\mathrm{2}} =\mathrm{V}_{\mathrm{H}} ^{\mathrm{2}} +\mathrm{4g}{l} \\ $$$$\mathrm{v}_{\mathrm{H}} ^{\mathrm{2}} =\frac{\mathrm{m}_{\mathrm{o}} ^{\mathrm{2}} \mathrm{u}_{\mathrm{o}} ^{\mathrm{2}} }{\mathrm{16M}}\:\:−\mathrm{4g}{l}\:\:\:…..\left(\mathrm{iii}\right) \\ $$$${for}\:{any}\:{particle}\:{to}\:{complete}\:{a} \\ $$$${circle}\:{safely} \\ $$$$\frac{{mv}_{{H}} ^{\mathrm{2}} }{\mathrm{r}}>\mathrm{mg} \\ $$$$\frac{{v}_{{H}} ^{\mathrm{2}} }{\mathrm{r}}>\mathrm{g} \\ $$$$\mathrm{v}_{\mathrm{H}} ^{\mathrm{2}} >\mathrm{gr}\:\:\:…..\left(\mathrm{iv}\right) \\ $$$$\frac{\mathrm{m}_{\mathrm{o}} ^{\mathrm{2}} \mathrm{u}_{\mathrm{o}} ^{\mathrm{2}} }{\mathrm{16M}}\:\:−\mathrm{4g}{l}\:>\mathrm{gr}\:\left[\mathrm{r}={l}\right] \\ $$$$\frac{\mathrm{m}_{\mathrm{o}} ^{\mathrm{2}} \mathrm{u}_{\mathrm{o}} ^{\mathrm{2}} }{\mathrm{16M}}\:>\mathrm{5g}{l} \\ $$$$\mathrm{m}_{\mathrm{o}} ^{\mathrm{2}} \mathrm{u}_{\mathrm{o}} ^{\mathrm{2}} >\mathrm{80Mg}{l} \\ $$$$\mathrm{u}_{\mathrm{o}} >\frac{\sqrt{\mathrm{80Mg}{l}}}{\mathrm{m}_{\mathrm{o}} } \\ $$$$\mathrm{u}_{\mathrm{o}} >\frac{\mathrm{4M}\sqrt{\mathrm{5g}{l}}}{{m}_{{o}} } \\ $$$$\mathrm{u}_{\mathrm{o}} =\frac{\mathrm{4M}\sqrt{\mathrm{5g}{l}}}{{m}_{{o}} } \\ $$
