Question Number 155035 by peter frank last updated on 24/Sep/21

Answered by mr W last updated on 24/Sep/21
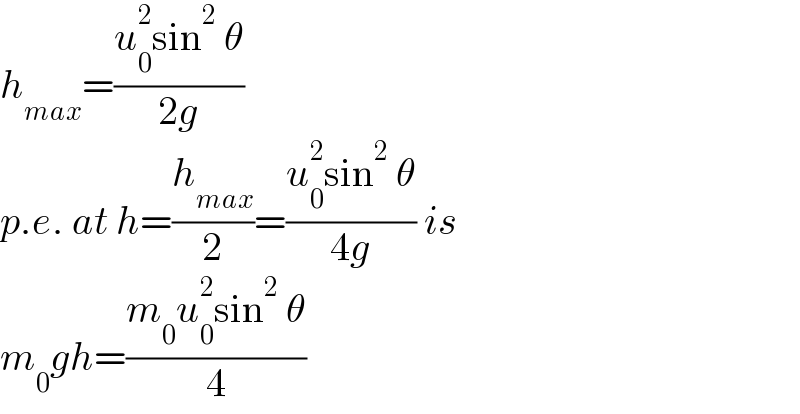
$${h}_{{max}} =\frac{{u}_{\mathrm{0}} ^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta}{\mathrm{2}{g}} \\ $$$${p}.{e}.\:{at}\:{h}=\frac{{h}_{{max}} }{\mathrm{2}}=\frac{{u}_{\mathrm{0}} ^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta}{\mathrm{4}{g}}\:{is} \\ $$$${m}_{\mathrm{0}} {gh}=\frac{{m}_{\mathrm{0}} {u}_{\mathrm{0}} ^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta}{\mathrm{4}} \\ $$
Commented by peter frank last updated on 25/Sep/21

$$\mathrm{thank}\:\mathrm{you} \\ $$
