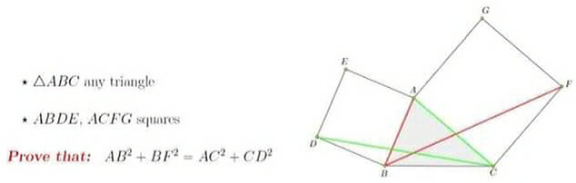
Question Number 155056 by mathdanisur last updated on 24/Sep/21
Answered by mr W last updated on 24/Sep/21
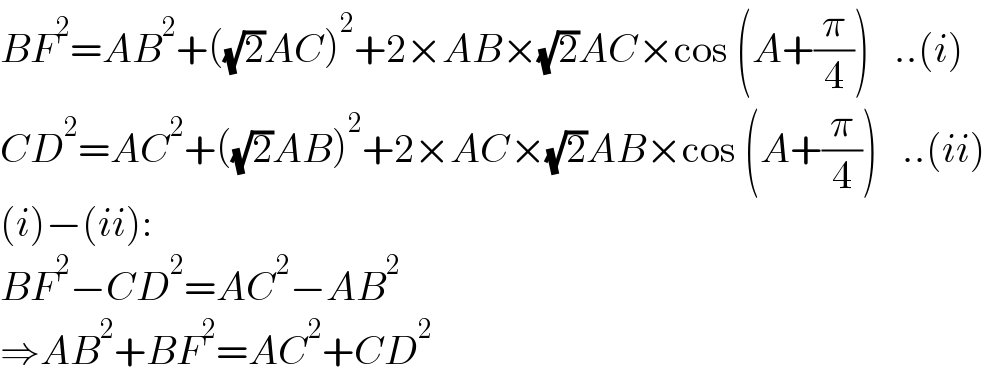
$${BF}^{\mathrm{2}} ={AB}^{\mathrm{2}} +\left(\sqrt{\mathrm{2}}{AC}\right)^{\mathrm{2}} +\mathrm{2}×{AB}×\sqrt{\mathrm{2}}{AC}×\mathrm{cos}\:\left({A}+\frac{\pi}{\mathrm{4}}\right)\:\:\:..\left({i}\right) \\ $$$${CD}^{\mathrm{2}} ={AC}^{\mathrm{2}} +\left(\sqrt{\mathrm{2}}{AB}\right)^{\mathrm{2}} +\mathrm{2}×{AC}×\sqrt{\mathrm{2}}{AB}×\mathrm{cos}\:\left({A}+\frac{\pi}{\mathrm{4}}\right)\:\:\:..\left({ii}\right) \\ $$$$\left({i}\right)−\left({ii}\right): \\ $$$${BF}^{\mathrm{2}} −{CD}^{\mathrm{2}} ={AC}^{\mathrm{2}} −{AB}^{\mathrm{2}} \\ $$$$\Rightarrow{AB}^{\mathrm{2}} +{BF}^{\mathrm{2}} ={AC}^{\mathrm{2}} +{CD}^{\mathrm{2}} \\ $$
Commented by mathdanisur last updated on 24/Sep/21
$$\mathrm{very}\:\mathrm{nice}\:\mathrm{Ser}\:\mathrm{thank}\:\mathrm{you} \\ $$
