Menu Close

Question-155075

Tinku Tara 0 Comments
Pin




Question Number 155075 by mr W last updated on 24/Sep/21
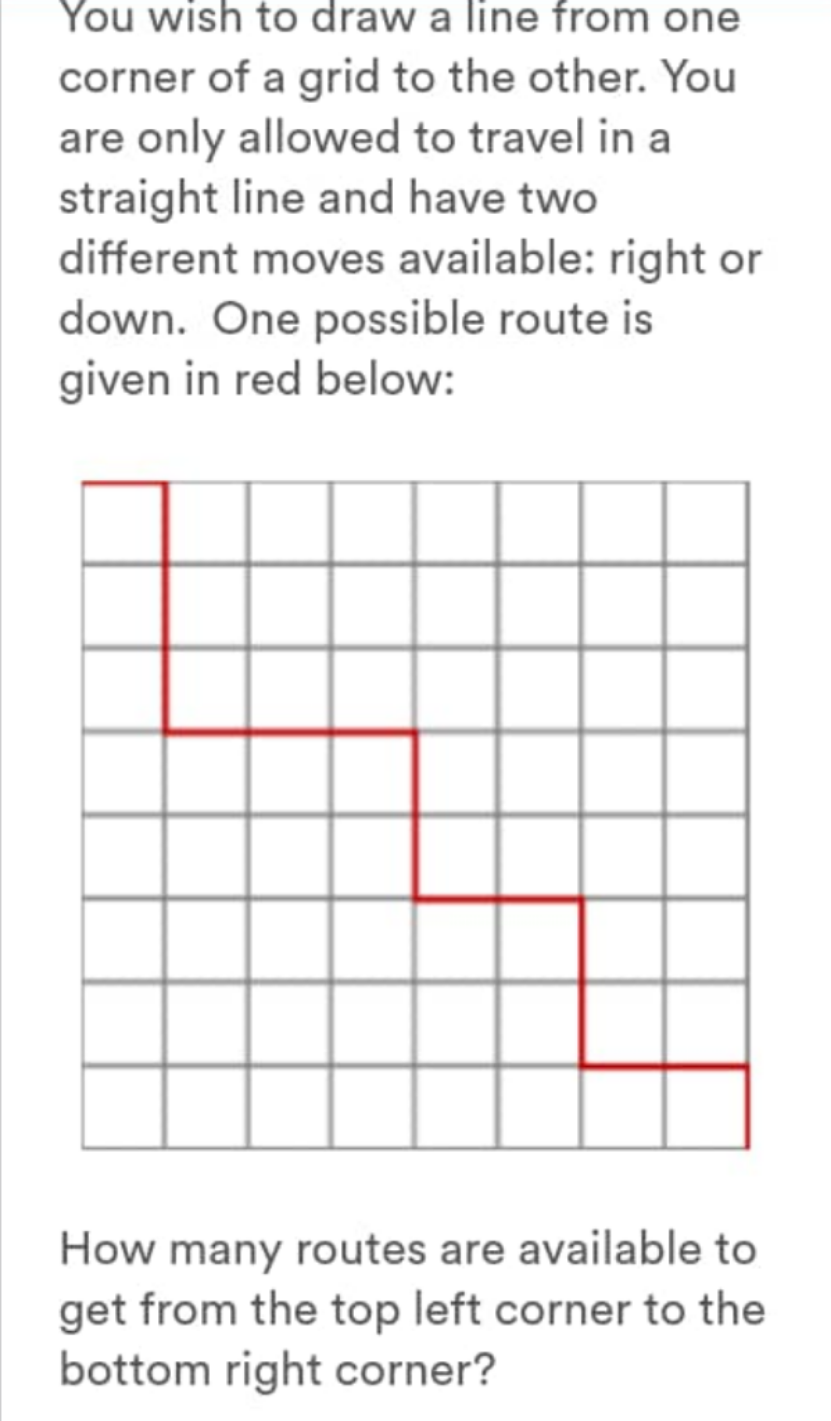
Commented by mr W last updated on 24/Sep/21
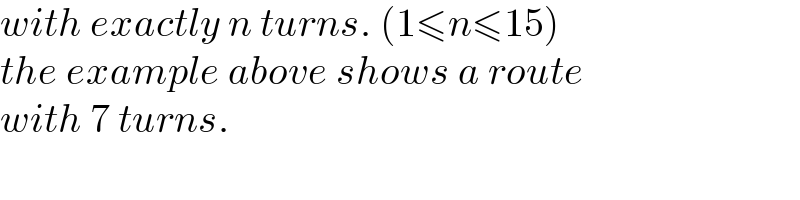
with exactly n turns. (1≤n≤15) the example above shows a route with 7 turns.
$${with}\:{exactly}\:{n}\:{turns}.\:\left(\mathrm{1}\leqslant{n}\leqslant\mathrm{15}\right) \\ $$$${the}\:{example}\:{above}\:{shows}\:{a}\:{route} \\ $$$${with}\:\mathrm{7}\:{turns}. \\ $$
Commented by Tawa11 last updated on 25/Sep/21
I will love to see sir
$$\mathrm{I}\:\mathrm{will}\:\mathrm{love}\:\mathrm{to}\:\mathrm{see}\:\mathrm{sir} \\ $$
Commented by Tawa11 last updated on 25/Sep/21
What of general formular for m × n grid. What is the generalization
$$\mathrm{What}\:\mathrm{of}\:\mathrm{general}\:\mathrm{formular}\:\mathrm{for}\:\:\:\:\:\mathrm{m}\:\:×\:\:\mathrm{n}\:\:\:\:\:\mathrm{grid}. \\ $$$$\mathrm{What}\:\mathrm{is}\:\mathrm{the}\:\mathrm{generalization} \\ $$
Commented by qaz last updated on 25/Sep/21
(((n+m)),(( m)) )
$$\begin{pmatrix}{\mathrm{n}+\mathrm{m}}\\{\:\:\mathrm{m}}\end{pmatrix} \\ $$
Answered by mr W last updated on 25/Sep/21
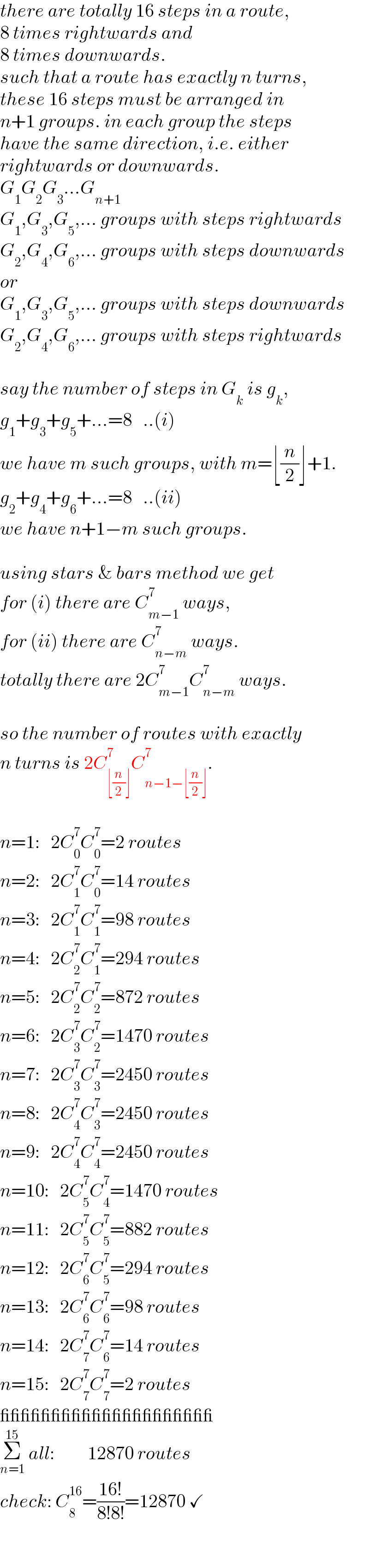
there are totally 16 steps in a route, 8 times rightwards and 8 times downwards. such that a route has exactly n turns, these 16 steps must be arranged in n+1 groups. in each group the steps have the same direction, i.e. either rightwards or downwards. G_1 G_2 G_3 ...G_(n+1) G_1 ,G_3 ,G_5 ,... groups with steps rightwards G_2 ,G_4 ,G_6 ,... groups with steps downwards or G_1 ,G_3 ,G_5 ,... groups with steps downwards G_2 ,G_4 ,G_6 ,... groups with steps rightwards say the number of steps in G_k is g_k , g_1 +g_3 +g_5 +...=8 ..(i) we have m such groups, with m=⌊(n/2)⌋+1. g_2 +g_4 +g_6 +...=8 ..(ii) we have n+1−m such groups. using stars & bars method we get for (i) there are C_(m−1) ^7 ways, for (ii) there are C_(n−m) ^7 ways. totally there are 2C_(m−1) ^7 C_(n−m) ^7 ways. so the number of routes with exactly n turns is 2C_(⌊(n/2)⌋) ^7 C_(n−1−⌊(n/2)⌋) ^7 . n=1: 2C_0 ^7 C_0 ^7 =2 routes n=2: 2C_1 ^7 C_0 ^7 =14 routes n=3: 2C_1 ^7 C_1 ^7 =98 routes n=4: 2C_2 ^7 C_1 ^7 =294 routes n=5: 2C_2 ^7 C_2 ^7 =872 routes n=6: 2C_3 ^7 C_2 ^7 =1470 routes n=7: 2C_3 ^7 C_3 ^7 =2450 routes n=8: 2C_4 ^7 C_3 ^7 =2450 routes n=9: 2C_4 ^7 C_4 ^7 =2450 routes n=10: 2C_5 ^7 C_4 ^7 =1470 routes n=11: 2C_5 ^7 C_5 ^7 =882 routes n=12: 2C_6 ^7 C_5 ^7 =294 routes n=13: 2C_6 ^7 C_6 ^7 =98 routes n=14: 2C_7 ^7 C_6 ^7 =14 routes n=15: 2C_7 ^7 C_7 ^7 =2 routes _____________________ Σ_(n=1) ^(15) all: 12870 routes check: C_8 ^(16) =((16!)/(8!8!))=12870 ✓
$${there}\:{are}\:{totally}\:\mathrm{16}\:{steps}\:{in}\:{a}\:{route},\: \\ $$$$\mathrm{8}\:{times}\:{rightwards}\:{and} \\ $$$$\mathrm{8}\:{times}\:{downwards}. \\ $$$${such}\:{that}\:{a}\:{route}\:{has}\:{exactly}\:{n}\:{turns}, \\ $$$${these}\:\mathrm{16}\:{steps}\:{must}\:{be}\:{arranged}\:{in} \\ $$$${n}+\mathrm{1}\:{groups}.\:{in}\:{each}\:{group}\:{the}\:{steps} \\ $$$${have}\:{the}\:{same}\:{direction},\:{i}.{e}.\:{either}\: \\ $$$${rightwards}\:{or}\:{downwards}. \\ $$$${G}_{\mathrm{1}} {G}_{\mathrm{2}} {G}_{\mathrm{3}} …{G}_{{n}+\mathrm{1}} \\ $$$${G}_{\mathrm{1}} ,{G}_{\mathrm{3}} ,{G}_{\mathrm{5}} ,…\:{groups}\:{with}\:{steps}\:{rightwards} \\ $$$${G}_{\mathrm{2}} ,{G}_{\mathrm{4}} ,{G}_{\mathrm{6}} ,…\:{groups}\:{with}\:{steps}\:{downwards} \\ $$$${or} \\ $$$${G}_{\mathrm{1}} ,{G}_{\mathrm{3}} ,{G}_{\mathrm{5}} ,…\:{groups}\:{with}\:{steps}\:{downwards} \\ $$$${G}_{\mathrm{2}} ,{G}_{\mathrm{4}} ,{G}_{\mathrm{6}} ,…\:{groups}\:{with}\:{steps}\:{rightwards} \\ $$$$ \\ $$$${say}\:{the}\:{number}\:{of}\:{steps}\:{in}\:{G}_{{k}} \:{is}\:{g}_{{k}} , \\ $$$${g}_{\mathrm{1}} +{g}_{\mathrm{3}} +{g}_{\mathrm{5}} +…=\mathrm{8}\:\:\:..\left({i}\right) \\ $$$${we}\:{have}\:{m}\:{such}\:{groups},\:{with}\:{m}=\lfloor\frac{{n}}{\mathrm{2}}\rfloor+\mathrm{1}. \\ $$$${g}_{\mathrm{2}} +{g}_{\mathrm{4}} +{g}_{\mathrm{6}} +…=\mathrm{8}\:\:\:..\left({ii}\right) \\ $$$${we}\:{have}\:{n}+\mathrm{1}−{m}\:{such}\:{groups}. \\ $$$$ \\ $$$${using}\:{stars}\:\&\:{bars}\:{method}\:{we}\:{get} \\ $$$${for}\:\left({i}\right)\:{there}\:{are}\:{C}_{{m}−\mathrm{1}} ^{\mathrm{7}} \:{ways},\: \\ $$$${for}\:\left({ii}\right)\:{there}\:{are}\:{C}_{{n}−{m}} ^{\mathrm{7}} \:{ways}.\: \\ $$$${totally}\:{there}\:{are}\:\mathrm{2}{C}_{{m}−\mathrm{1}} ^{\mathrm{7}} {C}_{{n}−{m}} ^{\mathrm{7}} \:{ways}. \\ $$$$ \\ $$$${so}\:{the}\:{number}\:{of}\:{routes}\:{with}\:{exactly} \\ $$$${n}\:{turns}\:{is}\:\mathrm{2}{C}_{\lfloor\frac{{n}}{\mathrm{2}}\rfloor} ^{\mathrm{7}} {C}_{{n}−\mathrm{1}−\lfloor\frac{{n}}{\mathrm{2}}\rfloor} ^{\mathrm{7}} . \\ $$$$ \\ $$$${n}=\mathrm{1}:\:\:\:\mathrm{2}{C}_{\mathrm{0}} ^{\mathrm{7}} {C}_{\mathrm{0}} ^{\mathrm{7}} =\mathrm{2}\:{routes} \\ $$$${n}=\mathrm{2}:\:\:\:\mathrm{2}{C}_{\mathrm{1}} ^{\mathrm{7}} {C}_{\mathrm{0}} ^{\mathrm{7}} =\mathrm{14}\:{routes} \\ $$$${n}=\mathrm{3}:\:\:\:\mathrm{2}{C}_{\mathrm{1}} ^{\mathrm{7}} {C}_{\mathrm{1}} ^{\mathrm{7}} =\mathrm{98}\:{routes} \\ $$$${n}=\mathrm{4}:\:\:\:\mathrm{2}{C}_{\mathrm{2}} ^{\mathrm{7}} {C}_{\mathrm{1}} ^{\mathrm{7}} =\mathrm{294}\:{routes} \\ $$$${n}=\mathrm{5}:\:\:\:\mathrm{2}{C}_{\mathrm{2}} ^{\mathrm{7}} {C}_{\mathrm{2}} ^{\mathrm{7}} =\mathrm{872}\:{routes} \\ $$$${n}=\mathrm{6}:\:\:\:\mathrm{2}{C}_{\mathrm{3}} ^{\mathrm{7}} {C}_{\mathrm{2}} ^{\mathrm{7}} =\mathrm{1470}\:{routes} \\ $$$${n}=\mathrm{7}:\:\:\:\mathrm{2}{C}_{\mathrm{3}} ^{\mathrm{7}} {C}_{\mathrm{3}} ^{\mathrm{7}} =\mathrm{2450}\:{routes} \\ $$$${n}=\mathrm{8}:\:\:\:\mathrm{2}{C}_{\mathrm{4}} ^{\mathrm{7}} {C}_{\mathrm{3}} ^{\mathrm{7}} =\mathrm{2450}\:{routes} \\ $$$${n}=\mathrm{9}:\:\:\:\mathrm{2}{C}_{\mathrm{4}} ^{\mathrm{7}} {C}_{\mathrm{4}} ^{\mathrm{7}} =\mathrm{2450}\:{routes} \\ $$$${n}=\mathrm{10}:\:\:\:\mathrm{2}{C}_{\mathrm{5}} ^{\mathrm{7}} {C}_{\mathrm{4}} ^{\mathrm{7}} =\mathrm{1470}\:{routes} \\ $$$${n}=\mathrm{11}:\:\:\:\mathrm{2}{C}_{\mathrm{5}} ^{\mathrm{7}} {C}_{\mathrm{5}} ^{\mathrm{7}} =\mathrm{882}\:{routes} \\ $$$${n}=\mathrm{12}:\:\:\:\mathrm{2}{C}_{\mathrm{6}} ^{\mathrm{7}} {C}_{\mathrm{5}} ^{\mathrm{7}} =\mathrm{294}\:{routes} \\ $$$${n}=\mathrm{13}:\:\:\:\mathrm{2}{C}_{\mathrm{6}} ^{\mathrm{7}} {C}_{\mathrm{6}} ^{\mathrm{7}} =\mathrm{98}\:{routes} \\ $$$${n}=\mathrm{14}:\:\:\:\mathrm{2}{C}_{\mathrm{7}} ^{\mathrm{7}} {C}_{\mathrm{6}} ^{\mathrm{7}} =\mathrm{14}\:{routes} \\ $$$${n}=\mathrm{15}:\:\:\:\mathrm{2}{C}_{\mathrm{7}} ^{\mathrm{7}} {C}_{\mathrm{7}} ^{\mathrm{7}} =\mathrm{2}\:{routes} \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\mathrm{15}} {\sum}}\:{all}:\:\:\:\:\:\:\:\:\:\mathrm{12870}\:{routes} \\ $$$${check}:\:{C}_{\mathrm{8}} ^{\mathrm{16}} =\frac{\mathrm{16}!}{\mathrm{8}!\mathrm{8}!}=\mathrm{12870}\:\checkmark \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *