Question Number 155130 by mathdanisur last updated on 25/Sep/21
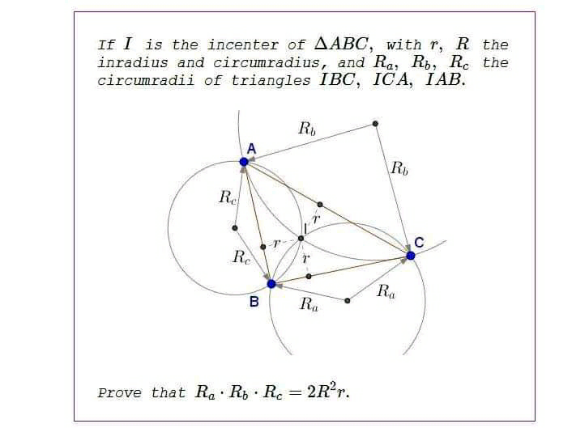
Answered by mr W last updated on 26/Sep/21

Commented by mathdanisur last updated on 26/Sep/21
$$\mathrm{Thank}\:\mathrm{you}\:\boldsymbol{\mathrm{S}}\mathrm{er},\:\mathrm{how}\:\mathrm{proved}\:\mathrm{please} \\ $$
Commented by mr W last updated on 26/Sep/21
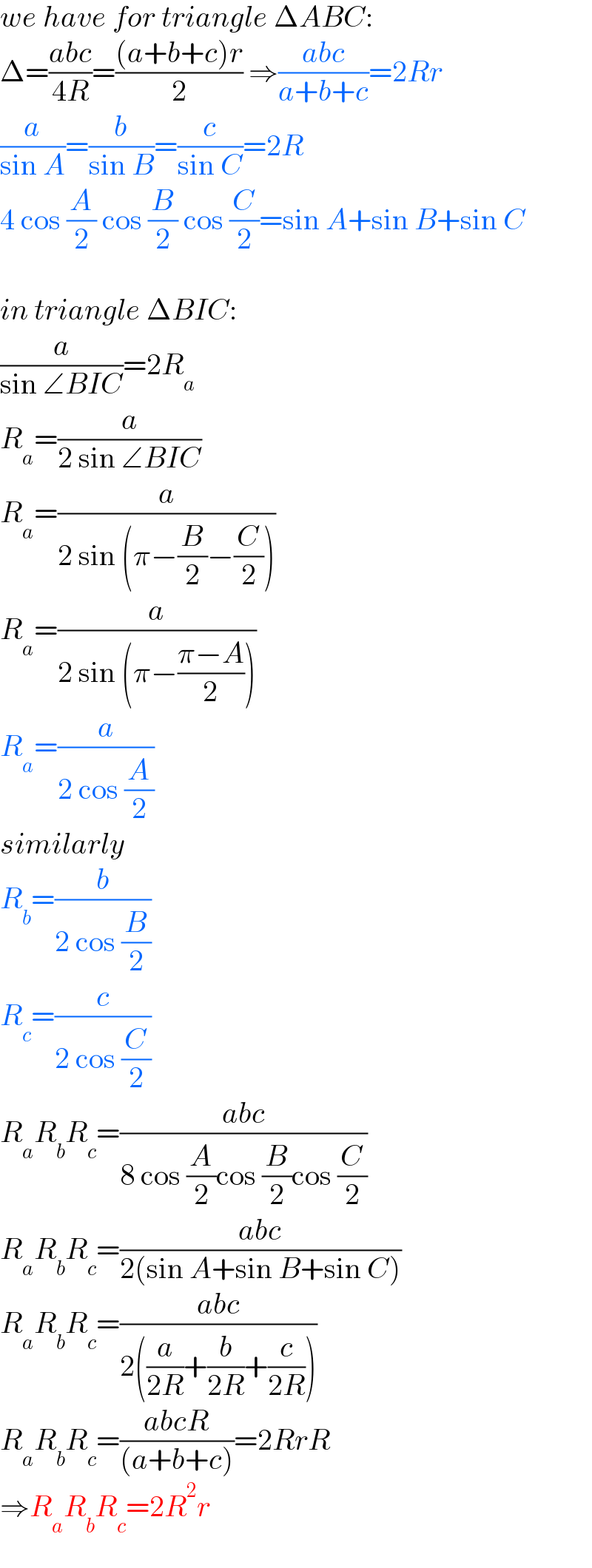
$${we}\:{have}\:{for}\:{triangle}\:\Delta{ABC}: \\ $$$$\Delta=\frac{{abc}}{\mathrm{4}{R}}=\frac{\left({a}+{b}+{c}\right){r}}{\mathrm{2}}\:\Rightarrow\frac{{abc}}{{a}+{b}+{c}}=\mathrm{2}{Rr} \\ $$$$\frac{{a}}{\mathrm{sin}\:{A}}=\frac{{b}}{\mathrm{sin}\:{B}}=\frac{{c}}{\mathrm{sin}\:{C}}=\mathrm{2}{R} \\ $$$$\mathrm{4}\:\mathrm{cos}\:\frac{{A}}{\mathrm{2}}\:\mathrm{cos}\:\frac{{B}}{\mathrm{2}}\:\mathrm{cos}\:\frac{{C}}{\mathrm{2}}=\mathrm{sin}\:{A}+\mathrm{sin}\:{B}+\mathrm{sin}\:{C} \\ $$$$ \\ $$$${in}\:{triangle}\:\Delta{BIC}: \\ $$$$\frac{{a}}{\mathrm{sin}\:\angle{BIC}}=\mathrm{2}{R}_{{a}} \\ $$$${R}_{{a}} =\frac{{a}}{\mathrm{2}\:\mathrm{sin}\:\angle{BIC}} \\ $$$${R}_{{a}} =\frac{{a}}{\mathrm{2}\:\mathrm{sin}\:\left(\pi−\frac{{B}}{\mathrm{2}}−\frac{{C}}{\mathrm{2}}\right)} \\ $$$${R}_{{a}} =\frac{{a}}{\mathrm{2}\:\mathrm{sin}\:\left(\pi−\frac{\pi−{A}}{\mathrm{2}}\right)} \\ $$$${R}_{{a}} =\frac{{a}}{\mathrm{2}\:\mathrm{cos}\:\frac{{A}}{\mathrm{2}}} \\ $$$${similarly} \\ $$$${R}_{{b}} =\frac{{b}}{\mathrm{2}\:\mathrm{cos}\:\frac{{B}}{\mathrm{2}}} \\ $$$${R}_{{c}} =\frac{{c}}{\mathrm{2}\:\mathrm{cos}\:\frac{{C}}{\mathrm{2}}} \\ $$$${R}_{{a}} {R}_{{b}} {R}_{{c}} =\frac{{abc}}{\mathrm{8}\:\mathrm{cos}\:\frac{{A}}{\mathrm{2}}\mathrm{cos}\:\frac{{B}}{\mathrm{2}}\mathrm{cos}\:\frac{{C}}{\mathrm{2}}} \\ $$$${R}_{{a}} {R}_{{b}} {R}_{{c}} =\frac{{abc}}{\mathrm{2}\left(\mathrm{sin}\:{A}+\mathrm{sin}\:{B}+\mathrm{sin}\:{C}\right)} \\ $$$${R}_{{a}} {R}_{{b}} {R}_{{c}} =\frac{{abc}}{\mathrm{2}\left(\frac{{a}}{\mathrm{2}{R}}+\frac{{b}}{\mathrm{2}{R}}+\frac{{c}}{\mathrm{2}{R}}\right)} \\ $$$${R}_{{a}} {R}_{{b}} {R}_{{c}} =\frac{{abcR}}{\left({a}+{b}+{c}\right)}=\mathrm{2}{RrR} \\ $$$$\Rightarrow{R}_{{a}} {R}_{{b}} {R}_{{c}} =\mathrm{2}{R}^{\mathrm{2}} {r} \\ $$
Commented by mathdanisur last updated on 26/Sep/21
$$\mathrm{awesome}\:\mathrm{solution},\:\mathrm{thank}\:\mathrm{you}\:\boldsymbol{\mathrm{S}}\mathrm{er} \\ $$
Commented by Tawa11 last updated on 26/Sep/21

$$\mathrm{great}\:\mathrm{sir} \\ $$
