Question Number 155165 by SANOGO last updated on 26/Sep/21

Answered by aleks041103 last updated on 26/Sep/21
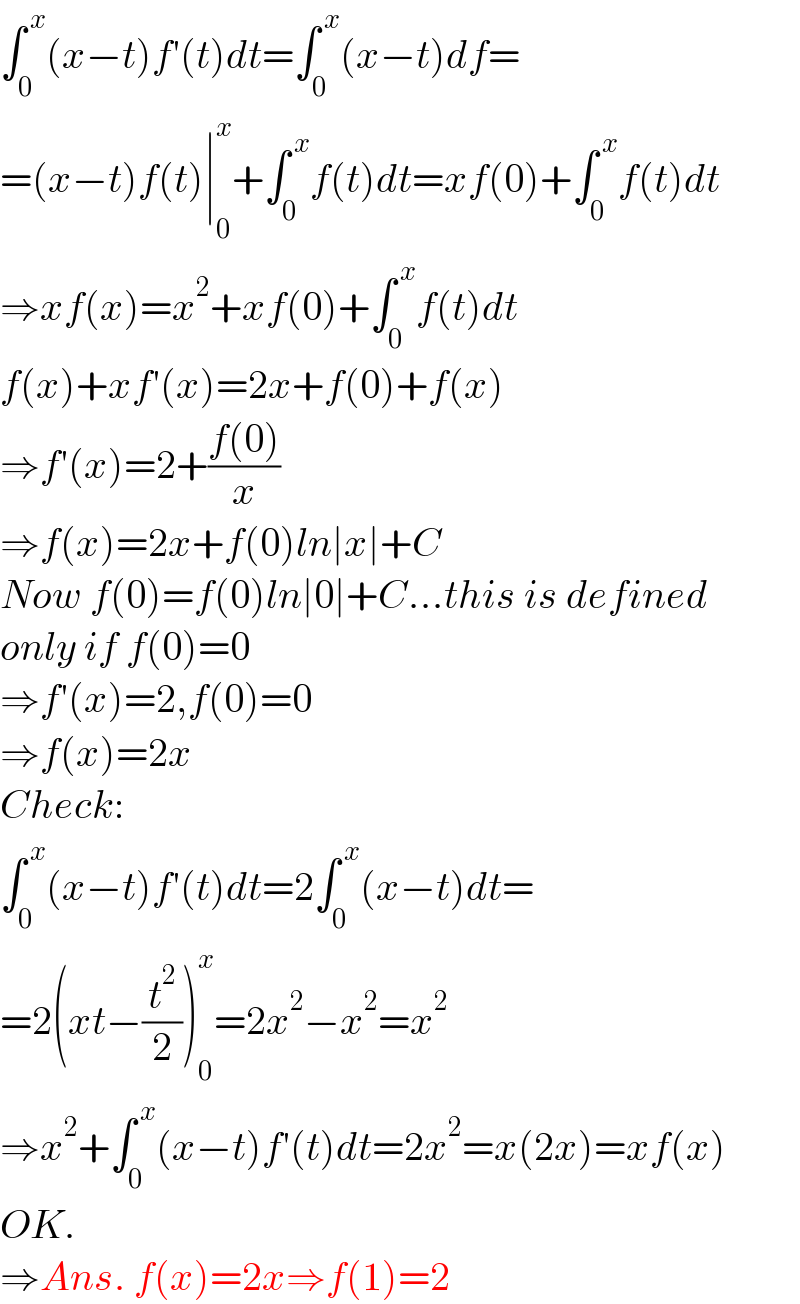
$$\int_{\mathrm{0}} ^{\:{x}} \left({x}−{t}\right){f}'\left({t}\right){dt}=\int_{\mathrm{0}} ^{\:{x}} \left({x}−{t}\right){df}= \\ $$$$=\left({x}−{t}\right){f}\left({t}\right)\mid_{\mathrm{0}} ^{{x}} +\int_{\mathrm{0}} ^{\:{x}} {f}\left({t}\right){dt}={xf}\left(\mathrm{0}\right)+\int_{\mathrm{0}} ^{\:{x}} {f}\left({t}\right){dt} \\ $$$$\Rightarrow{xf}\left({x}\right)={x}^{\mathrm{2}} +{xf}\left(\mathrm{0}\right)+\int_{\mathrm{0}} ^{\:{x}} {f}\left({t}\right){dt} \\ $$$${f}\left({x}\right)+{xf}'\left({x}\right)=\mathrm{2}{x}+{f}\left(\mathrm{0}\right)+{f}\left({x}\right) \\ $$$$\Rightarrow{f}'\left({x}\right)=\mathrm{2}+\frac{{f}\left(\mathrm{0}\right)}{{x}} \\ $$$$\Rightarrow{f}\left({x}\right)=\mathrm{2}{x}+{f}\left(\mathrm{0}\right){ln}\mid{x}\mid+{C} \\ $$$${Now}\:{f}\left(\mathrm{0}\right)={f}\left(\mathrm{0}\right){ln}\mid\mathrm{0}\mid+{C}…{this}\:{is}\:{defined} \\ $$$${only}\:{if}\:{f}\left(\mathrm{0}\right)=\mathrm{0} \\ $$$$\Rightarrow{f}'\left({x}\right)=\mathrm{2},{f}\left(\mathrm{0}\right)=\mathrm{0} \\ $$$$\Rightarrow{f}\left({x}\right)=\mathrm{2}{x} \\ $$$${Check}: \\ $$$$\int_{\mathrm{0}} ^{\:{x}} \left({x}−{t}\right){f}'\left({t}\right){dt}=\mathrm{2}\int_{\mathrm{0}} ^{\:{x}} \left({x}−{t}\right){dt}= \\ $$$$=\mathrm{2}\left({xt}−\frac{{t}^{\mathrm{2}} }{\mathrm{2}}\right)_{\mathrm{0}} ^{{x}} =\mathrm{2}{x}^{\mathrm{2}} −{x}^{\mathrm{2}} ={x}^{\mathrm{2}} \\ $$$$\Rightarrow{x}^{\mathrm{2}} +\int_{\mathrm{0}} ^{\:{x}} \left({x}−{t}\right){f}'\left({t}\right){dt}=\mathrm{2}{x}^{\mathrm{2}} ={x}\left(\mathrm{2}{x}\right)={xf}\left({x}\right) \\ $$$${OK}. \\ $$$$\Rightarrow{Ans}.\:{f}\left({x}\right)=\mathrm{2}{x}\Rightarrow{f}\left(\mathrm{1}\right)=\mathrm{2} \\ $$
Commented by SANOGO last updated on 26/Sep/21

$${merci}\:{bien} \\ $$
