Question Number 155215 by 0731619 last updated on 27/Sep/21

Answered by MJS_new last updated on 27/Sep/21

$${x}=\frac{\mathrm{1}}{\mathrm{2}}\wedge{y}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$
Commented by 0731619 last updated on 27/Sep/21

$${solution}??? \\ $$
Commented by MJS_new last updated on 27/Sep/21

$$\mathrm{sorry}\:\mathrm{it}'\mathrm{s}\:\mathrm{on}\:\mathrm{first}\:\mathrm{sight} \\ $$
Commented by 0731619 last updated on 27/Sep/21

$${plese}\:{solution} \\ $$
Answered by Rasheed.Sindhi last updated on 28/Sep/21
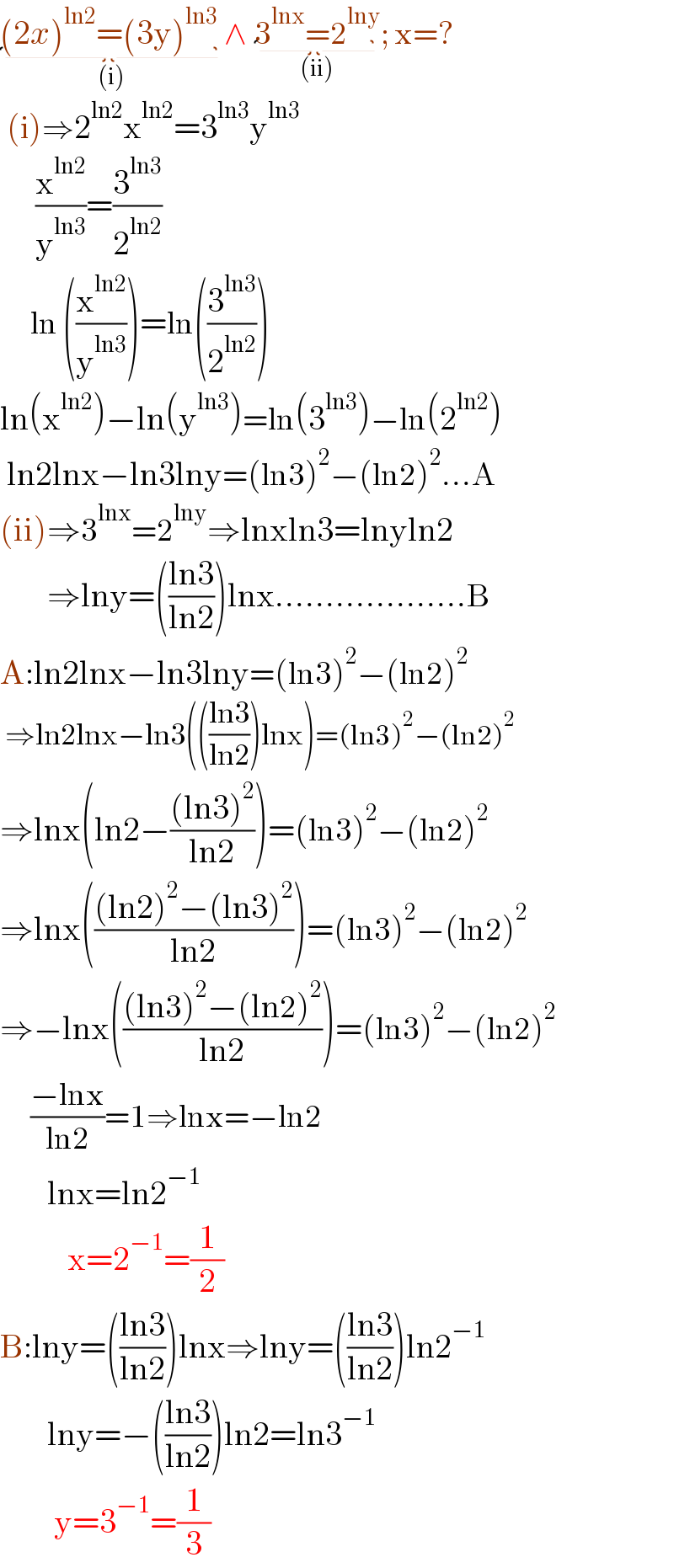
$$\underset{\left(\mathrm{i}\right)} {\underbrace{\left(\mathrm{2}{x}\right)^{\mathrm{ln2}} =\left(\mathrm{3y}\right)^{\mathrm{ln3}} \:}}\wedge\:\underset{\left(\mathrm{ii}\right)} {\underbrace{\mathrm{3}^{\mathrm{lnx}} =\mathrm{2}^{\mathrm{lny}} }};\:\mathrm{x}=? \\ $$$$\:\left(\mathrm{i}\right)\Rightarrow\mathrm{2}^{\mathrm{ln2}} \mathrm{x}^{\mathrm{ln2}} =\mathrm{3}^{\mathrm{ln3}} \mathrm{y}^{\mathrm{ln3}} \\ $$$$\:\:\:\:\:\:\:\frac{\mathrm{x}^{\mathrm{ln2}} }{\mathrm{y}^{\mathrm{ln3}} }=\frac{\mathrm{3}^{\mathrm{ln3}} }{\mathrm{2}^{\mathrm{ln2}} } \\ $$$$\:\:\:\:\:\:\mathrm{ln}\:\left(\frac{\mathrm{x}^{\mathrm{ln2}} }{\mathrm{y}^{\mathrm{ln3}} }\right)=\mathrm{ln}\left(\frac{\mathrm{3}^{\mathrm{ln3}} }{\mathrm{2}^{\mathrm{ln2}} }\right) \\ $$$$\mathrm{ln}\left(\mathrm{x}^{\mathrm{ln2}} \right)−\mathrm{ln}\left(\mathrm{y}^{\mathrm{ln3}} \right)=\mathrm{ln}\left(\mathrm{3}^{\mathrm{ln3}} \right)−\mathrm{ln}\left(\mathrm{2}^{\mathrm{ln2}} \right) \\ $$$$\:\mathrm{ln2lnx}−\mathrm{ln3lny}=\left(\mathrm{ln3}\right)^{\mathrm{2}} −\left(\mathrm{ln2}\right)^{\mathrm{2}} …\mathrm{A} \\ $$$$\left(\mathrm{ii}\right)\Rightarrow\mathrm{3}^{\mathrm{lnx}} =\mathrm{2}^{\mathrm{lny}} \Rightarrow\mathrm{lnxln3}=\mathrm{lnyln2} \\ $$$$\:\:\:\:\:\:\:\Rightarrow\mathrm{lny}=\left(\frac{\mathrm{ln3}}{\mathrm{ln2}}\right)\mathrm{lnx}……………….\mathrm{B}\: \\ $$$$\mathrm{A}:\mathrm{ln2lnx}−\mathrm{ln3lny}=\left(\mathrm{ln3}\right)^{\mathrm{2}} −\left(\mathrm{ln2}\right)^{\mathrm{2}} \\ $$$$\:\Rightarrow\mathrm{ln2lnx}−\mathrm{ln3}\left(\left(\frac{\mathrm{ln3}}{\mathrm{ln2}}\right)\mathrm{lnx}\right)=\left(\mathrm{ln3}\right)^{\mathrm{2}} −\left(\mathrm{ln2}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{lnx}\left(\mathrm{ln2}−\frac{\left(\mathrm{ln3}\right)^{\mathrm{2}} }{\mathrm{ln2}}\right)=\left(\mathrm{ln3}\right)^{\mathrm{2}} −\left(\mathrm{ln2}\right)^{\mathrm{2}} \:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\Rightarrow\mathrm{lnx}\left(\frac{\left(\mathrm{ln2}\right)^{\mathrm{2}} −\left(\mathrm{ln3}\right)^{\mathrm{2}} }{\mathrm{ln2}}\right)=\left(\mathrm{ln3}\right)^{\mathrm{2}} −\left(\mathrm{ln2}\right)^{\mathrm{2}} \:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\Rightarrow−\mathrm{lnx}\left(\frac{\left(\mathrm{ln3}\right)^{\mathrm{2}} −\left(\mathrm{ln2}\right)^{\mathrm{2}} }{\mathrm{ln2}}\right)=\left(\mathrm{ln3}\right)^{\mathrm{2}} −\left(\mathrm{ln2}\right)^{\mathrm{2}} \:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\frac{−\mathrm{lnx}}{\mathrm{ln2}}=\mathrm{1}\Rightarrow\mathrm{lnx}=−\mathrm{ln2} \\ $$$$\:\:\:\:\:\:\:\mathrm{lnx}=\mathrm{ln2}^{−\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{x}=\mathrm{2}^{−\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{B}:\mathrm{lny}=\left(\frac{\mathrm{ln3}}{\mathrm{ln2}}\right)\mathrm{lnx}\Rightarrow\mathrm{lny}=\left(\frac{\mathrm{ln3}}{\mathrm{ln2}}\right)\mathrm{ln2}^{−\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\mathrm{lny}=−\left(\frac{\mathrm{ln3}}{\mathrm{ln2}}\right)\mathrm{ln2}=\mathrm{ln3}^{−\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:\mathrm{y}=\mathrm{3}^{−\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{3}} \\ $$
Commented by Rasheed.Sindhi last updated on 28/Sep/21
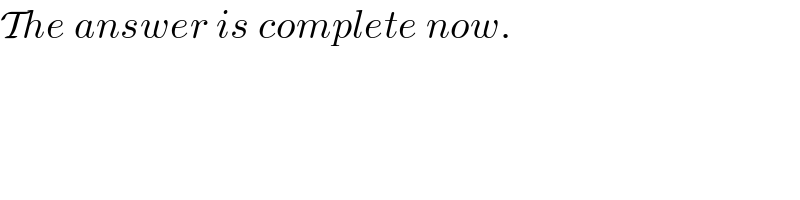
$$\mathcal{T}{he}\:{answer}\:{is}\:{complete}\:{now}. \\ $$
