Question Number 155225 by aliyn last updated on 27/Sep/21
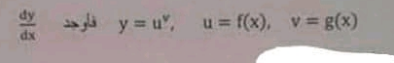
Commented by aliyn last updated on 27/Sep/21
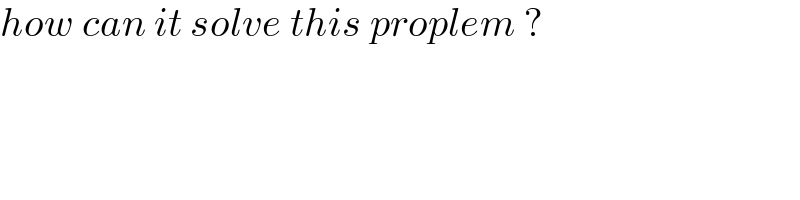
$${how}\:{can}\:{it}\:{solve}\:{this}\:{proplem}\:? \\ $$
Commented by bemath last updated on 27/Sep/21
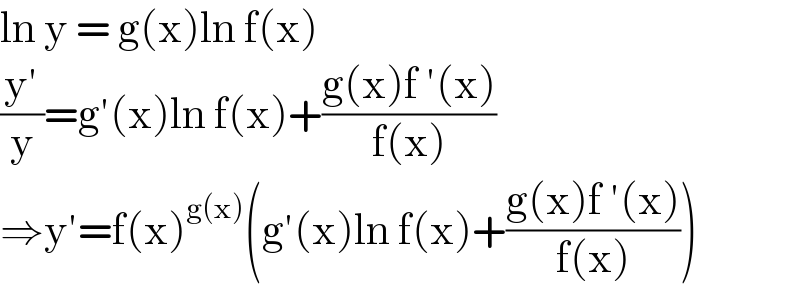
$$\mathrm{ln}\:\mathrm{y}\:=\:\mathrm{g}\left(\mathrm{x}\right)\mathrm{ln}\:\mathrm{f}\left(\mathrm{x}\right) \\ $$$$\frac{\mathrm{y}'}{\mathrm{y}}=\mathrm{g}'\left(\mathrm{x}\right)\mathrm{ln}\:\mathrm{f}\left(\mathrm{x}\right)+\frac{\mathrm{g}\left(\mathrm{x}\right)\mathrm{f}\:'\left(\mathrm{x}\right)}{\mathrm{f}\left(\mathrm{x}\right)} \\ $$$$\Rightarrow\mathrm{y}'=\mathrm{f}\left(\mathrm{x}\right)^{\mathrm{g}\left(\mathrm{x}\right)} \left(\mathrm{g}'\left(\mathrm{x}\right)\mathrm{ln}\:\mathrm{f}\left(\mathrm{x}\right)+\frac{\mathrm{g}\left(\mathrm{x}\right)\mathrm{f}\:'\left(\mathrm{x}\right)}{\mathrm{f}\left(\mathrm{x}\right)}\right) \\ $$
Commented by aliyn last updated on 27/Sep/21

$${thank}\:{you}\:{sir} \\ $$
