Question-155277

Question Number 155277 by amin96 last updated on 28/Sep/21

Answered by Rasheed.Sindhi last updated on 28/Sep/21

(big-square-area)−(non-shadow-area) big-square-area=8^2 =64 sq-units Non-shadow-area_(−) A:two-triangles=2((1/2).1.2)=2 unit^2 B:4{2^2 −(1/4)π(2)^2 }=4×((16−4π)/4)=16−4π C:2{4^2 −(1/4)π(4)^2 }=32−8π D(empty small squares):3(2^2 )=12 64−(A+B+C+D) =64−(2+16−4π+32−8π+12) =64−62+12π=2+12π

$$\left({big}-{square}-{area}\right)−\left({non}-{shadow}-{area}\right) \\ $$$${big}-{square}-{area}=\mathrm{8}^{\mathrm{2}} =\mathrm{64}\:{sq}-{units} \\ $$$$\:\:\:\:\:\:\underset{−} {{Non}-{shadow}-{area}} \\ $$$$\mathrm{A}:{two}-{triangles}=\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{2}}.\mathrm{1}.\mathrm{2}\right)=\mathrm{2}\:{unit}^{\mathrm{2}} \\ $$$$\mathrm{B}:\mathrm{4}\left\{\mathrm{2}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}\pi\left(\mathrm{2}\right)^{\mathrm{2}} \right\}=\mathrm{4}×\frac{\mathrm{16}−\mathrm{4}\pi}{\mathrm{4}}=\mathrm{16}−\mathrm{4}\pi \\ $$$$\mathrm{C}:\mathrm{2}\left\{\mathrm{4}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}\pi\left(\mathrm{4}\right)^{\mathrm{2}} \right\}=\mathrm{32}−\mathrm{8}\pi \\ $$$$\mathrm{D}\left({empty}\:{small}\:{squares}\right):\mathrm{3}\left(\mathrm{2}^{\mathrm{2}} \right)=\mathrm{12} \\ $$$$\mathrm{64}−\left(\mathrm{A}+\mathrm{B}+\mathrm{C}+\mathrm{D}\right) \\ $$$$\:\:\:\:=\mathrm{64}−\left(\mathrm{2}+\mathrm{16}−\mathrm{4}\pi+\mathrm{32}−\mathrm{8}\pi+\mathrm{12}\right) \\ $$$$\:\:\:=\mathrm{64}−\mathrm{62}+\mathrm{12}\pi=\mathrm{2}+\mathrm{12}\pi \\ $$

Commented by amin96 last updated on 28/Sep/21

B:4{2^2 −(1/4)π2^2 }=4((16−4π)/4)=16−4π C:2{4^2 −(1/4)π4^2 }=2((64−16π)/4)=32−8π shadow area =64−(16−4π+32−8π+12+2)= =64−62+12π=2+12π Sorry sir it has to be like that right?

$${B}:\mathrm{4}\left\{\mathrm{2}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}\pi\mathrm{2}^{\mathrm{2}} \right\}=\mathrm{4}\frac{\mathrm{16}−\mathrm{4}\pi}{\mathrm{4}}=\mathrm{16}−\mathrm{4}\pi \\ $$$${C}:\mathrm{2}\left\{\mathrm{4}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}\pi\mathrm{4}^{\mathrm{2}} \right\}=\mathrm{2}\frac{\mathrm{64}−\mathrm{16}\pi}{\mathrm{4}}=\mathrm{32}−\mathrm{8}\pi \\ $$$${shadow}\:{area}\:=\mathrm{64}−\left(\mathrm{16}−\mathrm{4}\pi+\mathrm{32}−\mathrm{8}\pi+\mathrm{12}+\mathrm{2}\right)= \\ $$$$=\mathrm{64}−\mathrm{62}+\mathrm{12}\pi=\mathrm{2}+\mathrm{12}\pi \\ $$$${Sorry}\:{sir}\:{it}\:{has}\:{to}\:{be}\:{like}\:{that}\:{right}? \\ $$

Commented by Rasheed.Sindhi last updated on 28/Sep/21

$${Sorry}\:{for}\:{my}\:{mistakes}\:{sir}.{I}'{ll}\:{edit} \\ $$$${my}\:{answer}. \\ $$

Answered by qaz last updated on 28/Sep/21

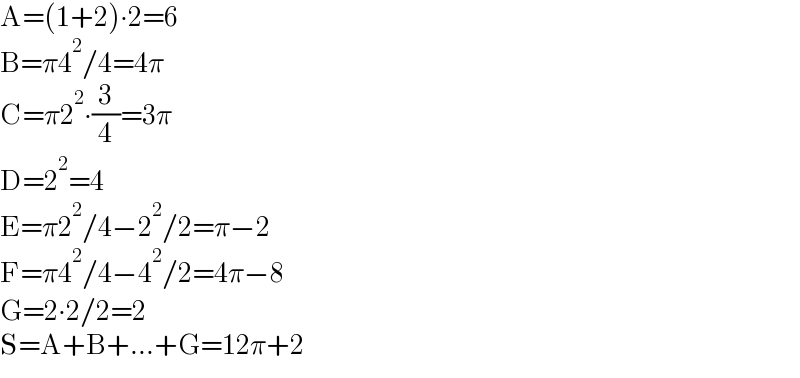
A=(1+2)∙2=6 B=π4^2 /4=4π C=π2^2 ∙(3/4)=3π D=2^2 =4 E=π2^2 /4−2^2 /2=π−2 F=π4^2 /4−4^2 /2=4π−8 G=2∙2/2=2 S=A+B+...+G=12π+2

$$\mathrm{A}=\left(\mathrm{1}+\mathrm{2}\right)\centerdot\mathrm{2}=\mathrm{6} \\ $$$$\mathrm{B}=\pi\mathrm{4}^{\mathrm{2}} /\mathrm{4}=\mathrm{4}\pi \\ $$$$\mathrm{C}=\pi\mathrm{2}^{\mathrm{2}} \centerdot\frac{\mathrm{3}}{\mathrm{4}}=\mathrm{3}\pi \\ $$$$\mathrm{D}=\mathrm{2}^{\mathrm{2}} =\mathrm{4} \\ $$$$\mathrm{E}=\pi\mathrm{2}^{\mathrm{2}} /\mathrm{4}−\mathrm{2}^{\mathrm{2}} /\mathrm{2}=\pi−\mathrm{2} \\ $$$$\mathrm{F}=\pi\mathrm{4}^{\mathrm{2}} /\mathrm{4}−\mathrm{4}^{\mathrm{2}} /\mathrm{2}=\mathrm{4}\pi−\mathrm{8} \\ $$$$\mathrm{G}=\mathrm{2}\centerdot\mathrm{2}/\mathrm{2}=\mathrm{2} \\ $$$$\mathrm{S}=\mathrm{A}+\mathrm{B}+…+\mathrm{G}=\mathrm{12}\pi+\mathrm{2} \\ $$

Commented by amin96 last updated on 28/Sep/21

$${thanks}\:{sir} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply