Question Number 155292 by peter frank last updated on 28/Sep/21

Answered by peter frank last updated on 30/Sep/21
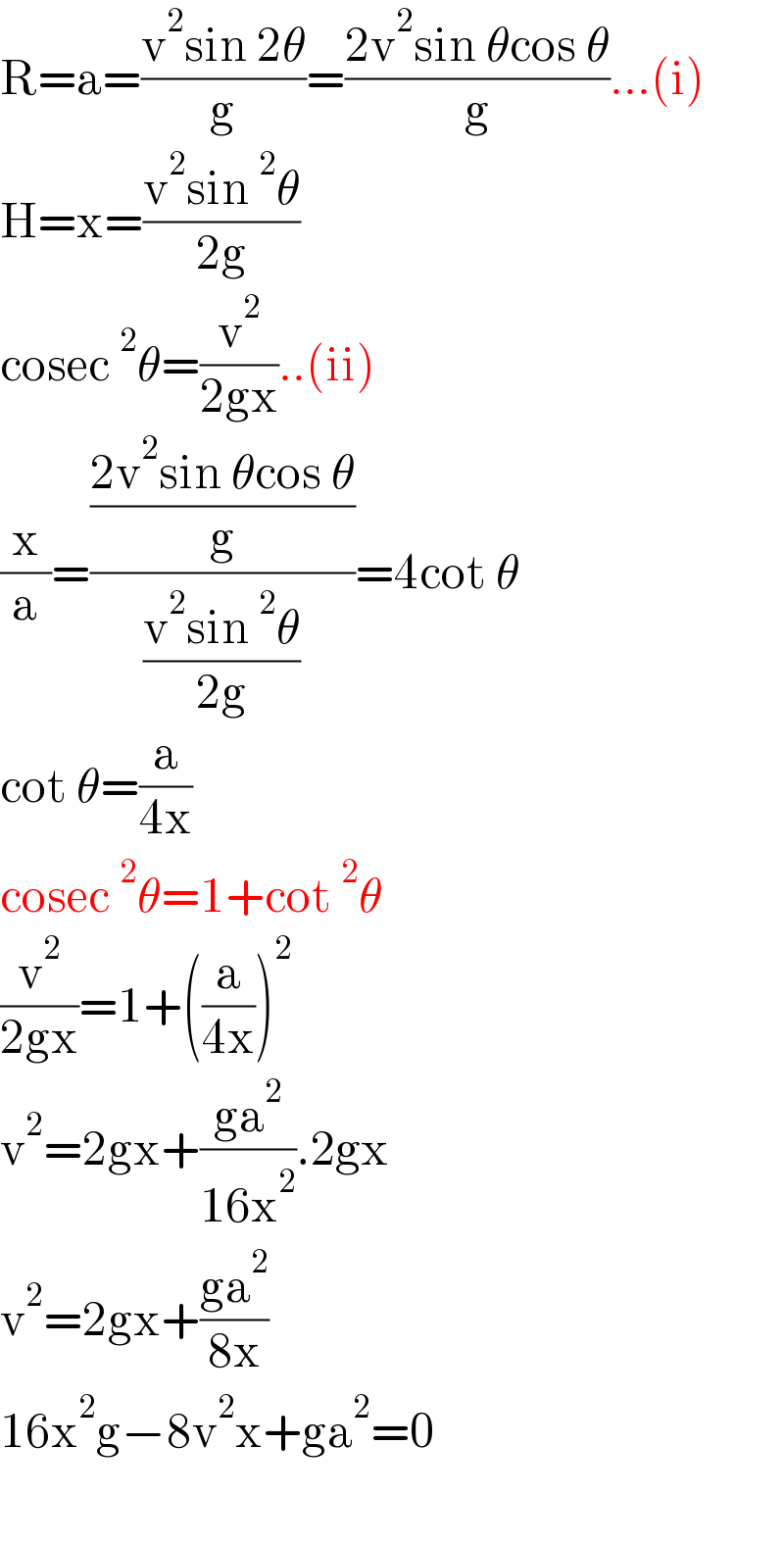
$$\mathrm{R}=\mathrm{a}=\frac{\mathrm{v}^{\mathrm{2}} \mathrm{sin}\:\mathrm{2}\theta}{\mathrm{g}}=\frac{\mathrm{2v}^{\mathrm{2}} \mathrm{sin}\:\theta\mathrm{cos}\:\theta}{\mathrm{g}}…\left(\mathrm{i}\right) \\ $$$$\mathrm{H}=\mathrm{x}=\frac{\mathrm{v}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta}{\mathrm{2g}} \\ $$$$\mathrm{cosec}\:^{\mathrm{2}} \theta=\frac{\mathrm{v}^{\mathrm{2}} }{\mathrm{2gx}}..\left(\mathrm{ii}\right) \\ $$$$\frac{\mathrm{x}}{\mathrm{a}}=\frac{\frac{\mathrm{2v}^{\mathrm{2}} \mathrm{sin}\:\theta\mathrm{cos}\:\theta}{\mathrm{g}}}{\frac{\mathrm{v}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta}{\mathrm{2g}}}=\mathrm{4cot}\:\theta \\ $$$$\mathrm{cot}\:\theta=\frac{\mathrm{a}}{\mathrm{4x}} \\ $$$$\mathrm{cosec}\:^{\mathrm{2}} \theta=\mathrm{1}+\mathrm{cot}\:^{\mathrm{2}} \theta \\ $$$$\frac{\mathrm{v}^{\mathrm{2}} }{\mathrm{2gx}}=\mathrm{1}+\left(\frac{\mathrm{a}}{\mathrm{4x}}\right)^{\mathrm{2}} \\ $$$$\mathrm{v}^{\mathrm{2}} =\mathrm{2gx}+\frac{\mathrm{ga}^{\mathrm{2}} }{\mathrm{16x}^{\mathrm{2}} }.\mathrm{2gx} \\ $$$$\mathrm{v}^{\mathrm{2}} =\mathrm{2gx}+\frac{\mathrm{ga}^{\mathrm{2}} }{\mathrm{8x}} \\ $$$$\mathrm{16x}^{\mathrm{2}} \mathrm{g}−\mathrm{8v}^{\mathrm{2}} \mathrm{x}+\mathrm{ga}^{\mathrm{2}} =\mathrm{0} \\ $$$$ \\ $$
