Question Number 155293 by peter frank last updated on 28/Sep/21

Answered by mr W last updated on 28/Sep/21

Commented by mr W last updated on 28/Sep/21
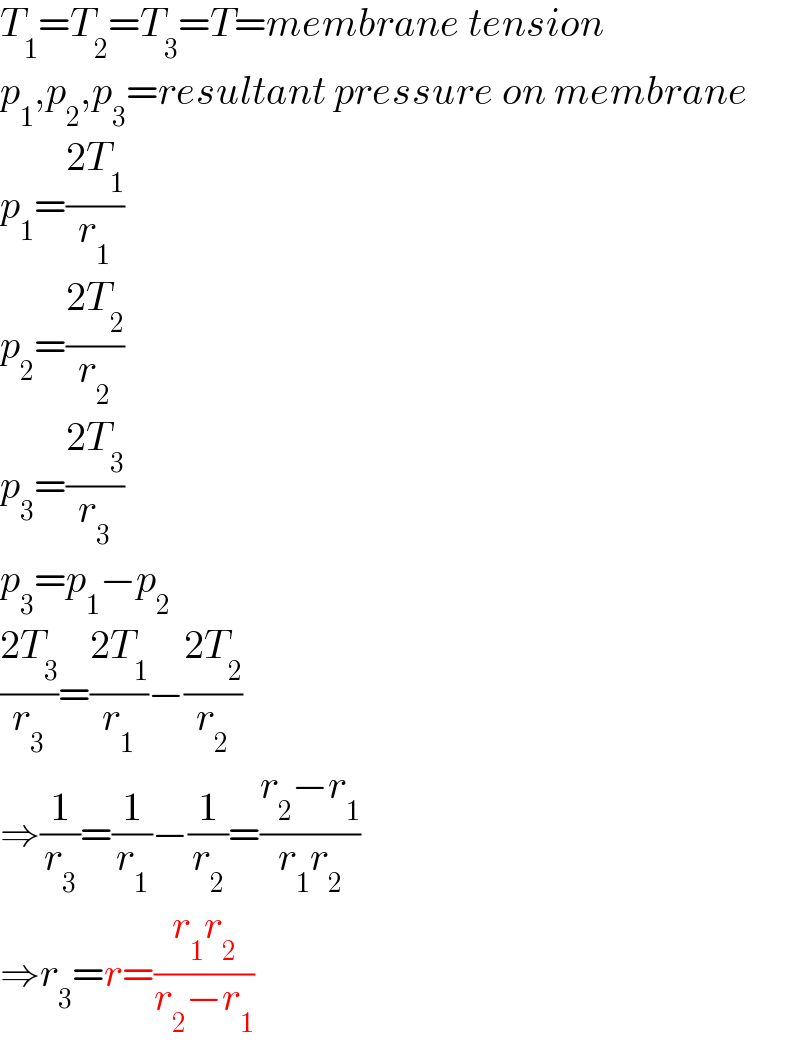
$${T}_{\mathrm{1}} ={T}_{\mathrm{2}} ={T}_{\mathrm{3}} ={T}={membrane}\:{tension} \\ $$$${p}_{\mathrm{1}} ,{p}_{\mathrm{2}} ,{p}_{\mathrm{3}} ={resultant}\:{pressure}\:{on}\:{membrane} \\ $$$${p}_{\mathrm{1}} =\frac{\mathrm{2}{T}_{\mathrm{1}} }{{r}_{\mathrm{1}} } \\ $$$${p}_{\mathrm{2}} =\frac{\mathrm{2}{T}_{\mathrm{2}} }{{r}_{\mathrm{2}} } \\ $$$${p}_{\mathrm{3}} =\frac{\mathrm{2}{T}_{\mathrm{3}} }{{r}_{\mathrm{3}} } \\ $$$${p}_{\mathrm{3}} ={p}_{\mathrm{1}} −{p}_{\mathrm{2}} \\ $$$$\frac{\mathrm{2}{T}_{\mathrm{3}} }{{r}_{\mathrm{3}} }=\frac{\mathrm{2}{T}_{\mathrm{1}} }{{r}_{\mathrm{1}} }−\frac{\mathrm{2}{T}_{\mathrm{2}} }{{r}_{\mathrm{2}} } \\ $$$$\Rightarrow\frac{\mathrm{1}}{{r}_{\mathrm{3}} }=\frac{\mathrm{1}}{{r}_{\mathrm{1}} }−\frac{\mathrm{1}}{{r}_{\mathrm{2}} }=\frac{{r}_{\mathrm{2}} −{r}_{\mathrm{1}} }{{r}_{\mathrm{1}} {r}_{\mathrm{2}} } \\ $$$$\Rightarrow{r}_{\mathrm{3}} ={r}=\frac{{r}_{\mathrm{1}} {r}_{\mathrm{2}} }{{r}_{\mathrm{2}} −{r}_{\mathrm{1}} } \\ $$
Commented by peter frank last updated on 28/Sep/21
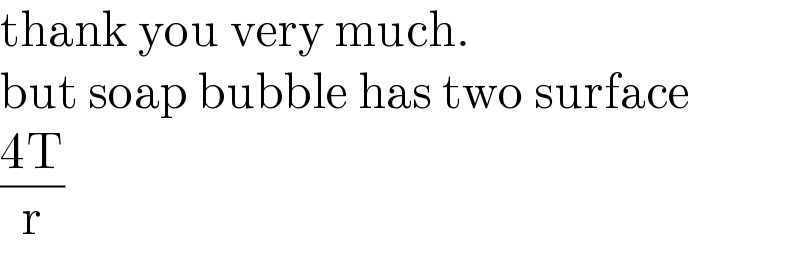
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}. \\ $$$$\mathrm{but}\:\mathrm{soap}\:\mathrm{bubble}\:\mathrm{has}\:\mathrm{two}\:\mathrm{surface} \\ $$$$\frac{\mathrm{4T}}{\mathrm{r}} \\ $$
Commented by mr W last updated on 28/Sep/21

$${i}\:{refere}\:{to}\:{the}\:{resultant}\:{force}\:{as}\:{if} \\ $$$${it}\:{is}\:{a}\:{membrane}\:{like}\:{a}\:{balloon}. \\ $$
Commented by peter frank last updated on 28/Sep/21

$$\mathrm{okay}. \\ $$
Commented by Tawa11 last updated on 28/Sep/21

$$\mathrm{Great}\:\mathrm{sirs} \\ $$
Answered by peter frank last updated on 28/Sep/21

Commented by peter frank last updated on 28/Sep/21

$$\mathrm{S}=\mathrm{common}\:\mathrm{interface} \\ $$$$\mathrm{H}=\mathrm{outside}\:\mathrm{pressure} \\ $$$$\mathrm{P}_{\mathrm{1}} \&\mathrm{P}_{\mathrm{2}} =\mathrm{inside}\:\mathrm{pressure}\:\mathrm{for}\:\mathrm{small} \\ $$$$\mathrm{and}\:\mathrm{large}\:\mathrm{bubble} \\ $$$$\gamma=\mathrm{surface}\:\mathrm{tension} \\ $$$$\underline{\boldsymbol{{For}}\:\boldsymbol{{small}}\:\boldsymbol{{bubble}}} \\ $$$$\mathrm{P}_{\mathrm{1}} −\mathrm{H}=\frac{\mathrm{4}\gamma}{\mathrm{r}_{\mathrm{1}} }\:\:\:….\left(\mathrm{i}\right) \\ $$$$\underline{\boldsymbol{{For}}\:\boldsymbol{{large}}\:\boldsymbol{{bubble}}\:} \\ $$$$\mathrm{P}_{\mathrm{2}} −\mathrm{H}=\frac{\mathrm{4}\gamma}{\mathrm{r}_{\mathrm{2}} }….\left(\mathrm{ii}\right) \\ $$$$\underline{\boldsymbol{{For}}\:\boldsymbol{{the}}\:\boldsymbol{{interface}}} \\ $$$$\mathrm{P}_{\mathrm{1}} −\mathrm{P}_{\mathrm{2}} =\frac{\mathrm{4}\gamma}{\mathrm{r}}\:….\left(\mathrm{iii}\right) \\ $$$$\left(\mathrm{i}\right)−\left(\mathrm{ii}\right) \\ $$$$\mathrm{P}_{\mathrm{1}} −\mathrm{P}_{\mathrm{2}} =\frac{\mathrm{4}\gamma}{\mathrm{r}_{\mathrm{1}} }−\frac{\mathrm{4}\gamma}{\mathrm{r}_{\mathrm{2}} } \\ $$$$\mathrm{but}\:\:\:\mathrm{P}_{\mathrm{1}} −\mathrm{P}_{\mathrm{2}} =\frac{\mathrm{4}\gamma}{\mathrm{r}}\: \\ $$$$\frac{\mathrm{4}\gamma}{\mathrm{r}}\:=\frac{\mathrm{4}\gamma}{\mathrm{r}_{\mathrm{1}} }−\frac{\mathrm{4}\gamma}{\mathrm{r}_{\mathrm{2}} } \\ $$$$\frac{\mathrm{1}}{\mathrm{r}}\:=\frac{\mathrm{1}}{\mathrm{r}_{\mathrm{1}} }−\frac{\mathrm{1}}{\mathrm{r}_{\mathrm{2}} } \\ $$$$\mathrm{r}=\frac{\mathrm{r}_{\mathrm{1}} \mathrm{r}_{\mathrm{2}} }{\mathrm{r}_{\mathrm{2}\:−} \mathrm{r}_{\mathrm{1}} } \\ $$
