Question Number 15534 by ajfour last updated on 11/Jun/17
Commented by ajfour last updated on 11/Jun/17

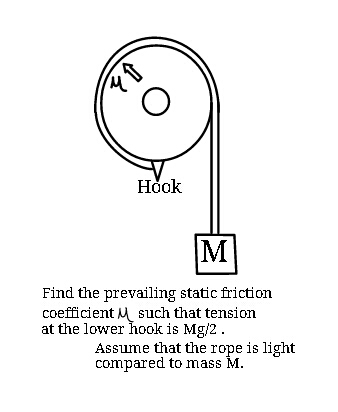
$$\:{Find}\:{the}\:{existing}\:{static}\:{friction} \\ $$$${coefficient}\:{between}\:{rope}\:{and} \\ $$$${pulley}\:{if}\:{the}\:{tension}\:{in}\:{rope}\:{at}\: \\ $$$${the}\:{hook}\:{to}\:{which}\:{it}'{s}\:{one}\:{end} \\ $$$${is}\:{tied}\:{is}\:{equal}\:{to}\:\frac{{Mg}}{\mathrm{2}}\:. \\ $$$${Assume}\:{mass}\:{of}\:{thread}\:{is} \\ $$$${negligible}\:{compared}\:{to}\:{the}\: \\ $$$${mass}\:{of}\:{the}\:{block}\:\left({M}\right). \\ $$
Answered by mrW1 last updated on 11/Jun/17
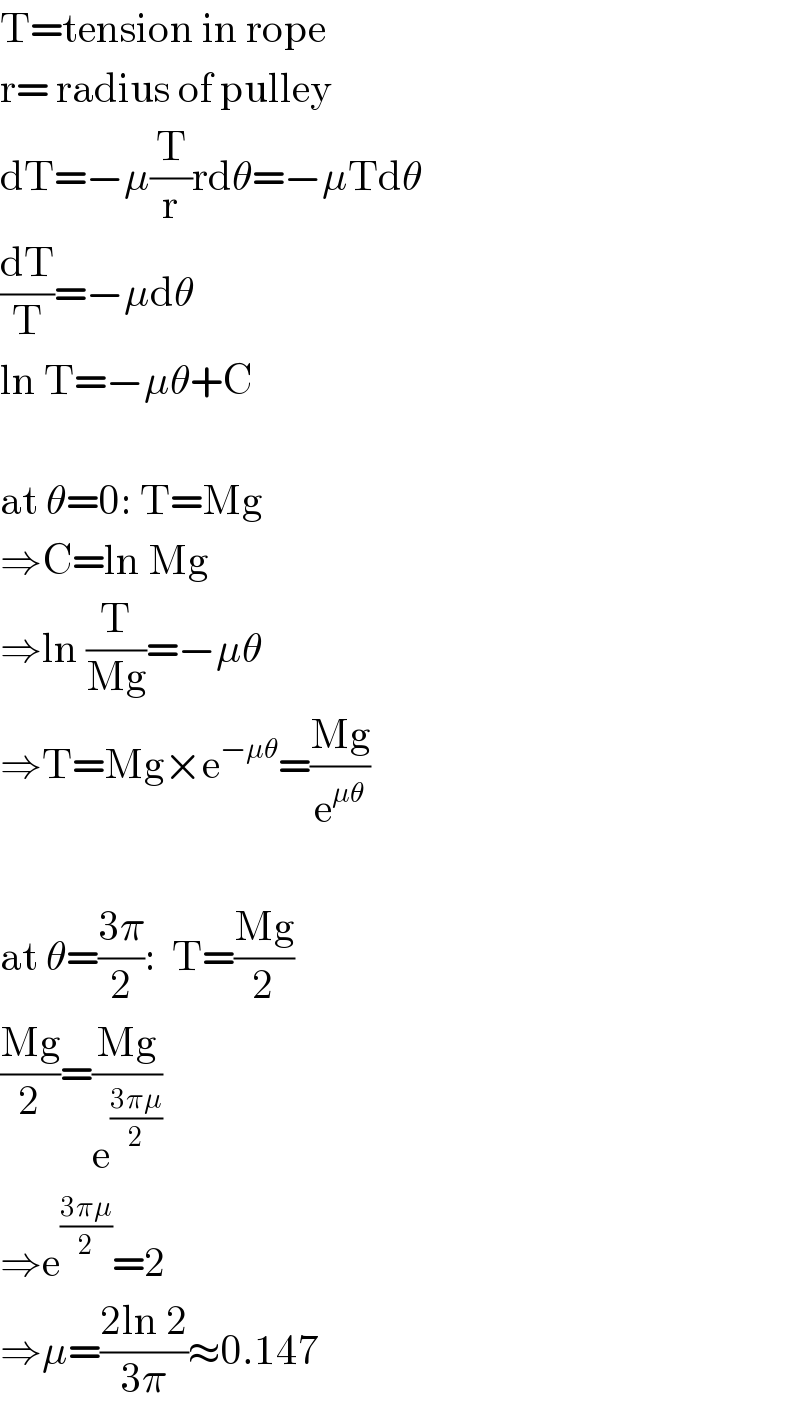
$$\mathrm{T}=\mathrm{tension}\:\mathrm{in}\:\mathrm{rope} \\ $$$$\mathrm{r}=\:\mathrm{radius}\:\mathrm{of}\:\mathrm{pulley} \\ $$$$\mathrm{dT}=−\mu\frac{\mathrm{T}}{\mathrm{r}}\mathrm{rd}\theta=−\mu\mathrm{Td}\theta \\ $$$$\frac{\mathrm{dT}}{\mathrm{T}}=−\mu\mathrm{d}\theta \\ $$$$\mathrm{ln}\:\mathrm{T}=−\mu\theta+\mathrm{C} \\ $$$$ \\ $$$$\mathrm{at}\:\theta=\mathrm{0}:\:\mathrm{T}=\mathrm{Mg} \\ $$$$\Rightarrow\mathrm{C}=\mathrm{ln}\:\mathrm{Mg} \\ $$$$\Rightarrow\mathrm{ln}\:\frac{\mathrm{T}}{\mathrm{Mg}}=−\mu\theta \\ $$$$\Rightarrow\mathrm{T}=\mathrm{Mg}×\mathrm{e}^{−\mu\theta} =\frac{\mathrm{Mg}}{\mathrm{e}^{\mu\theta} } \\ $$$$ \\ $$$$\mathrm{at}\:\theta=\frac{\mathrm{3}\pi}{\mathrm{2}}:\:\:\mathrm{T}=\frac{\mathrm{Mg}}{\mathrm{2}} \\ $$$$\frac{\mathrm{Mg}}{\mathrm{2}}=\frac{\mathrm{Mg}}{\mathrm{e}^{\frac{\mathrm{3}\pi\mu}{\mathrm{2}}} } \\ $$$$\Rightarrow\mathrm{e}^{\frac{\mathrm{3}\pi\mu}{\mathrm{2}}} =\mathrm{2} \\ $$$$\Rightarrow\mu=\frac{\mathrm{2ln}\:\mathrm{2}}{\mathrm{3}\pi}\approx\mathrm{0}.\mathrm{147} \\ $$
Commented by ajfour last updated on 11/Jun/17
$${thank}\:{you}\:{sir}.\:{answer}\:{is}\:{correct}. \\ $$
